Grothendieck category
|
Read other articles:

S-CRY-ed is an anime created by Sunrise. The plot is set in an alternate time where an earthquake known as the Great Uprising has divided a city in two sections: the Mainlands and the Lost Ground. One percent of the Lost Ground's people have developed supernatural powers known as Alter. The series follows a young mercenary known as Kazuma from the Lost Ground. While doing one of his jobs he encounters a man known as Ryuho, a member from the Mainland Alter special forces known as HOLY. There ...

Halaman ini berisi artikel tentang film Swedia. Untuk album karya Dominic Duval, lihat Cries and Whispers (album). Cries and WhispersPoster rilis teatrikal SwediaSutradaraIngmar BergmanProduserLars-Owe CarlbergDitulis olehIngmar BergmanPemeranHarriet AnderssonKari SylwanIngrid ThulinLiv UllmannInga GillErland JosephsonNaratorIngmar BergmanPenata musikJohann Sebastian BachFrédéric ChopinSinematograferSven NykvistPenyuntingSiv LundgrenPerusahaanproduksiSvensk FilmindustriDistributorNew ...

Bring It OnBring It OnSutradaraPeyton ReedProduserMarc Abraham, Thomas A. BlissDitulis olehJessica BendingerPemeranKirsten Dunst, Eliza Dushku, Jesse Bradford, Gabrielle UnionPenata musikChristophe BeckSinematograferShawn MaurerPenyuntingLarry BockDistributorUniversal PicturesBeacon CommunicationsTanggal rilis22 Agustus 2000Durasi98 menitBahasaInggrisAnggaranUSD$10.000.000Pendapatankotor$90.449.929SekuelBring It On AgainIMDbInformasi di IMDb Bring It On adalah sebuah film komedi remaja ...

1573–74 battle of the Anglo-Spanish War Siege of LeidenPart of the Eighty Years' War & the Anglo–Spanish WarRelief of Leiden by the Geuzen on flat-bottomed boats, on 3 October 1574. Otto van Veen.DateOctober 1573 – 3 October 1574LocationLeiden (present-day Netherlands)52°09′00″N 4°29′00″E / 52.1500°N 4.4833°E / 52.1500; 4.4833Result Dutch victoryBelligerents Dutch Rebels England French Huguenots Scotland SpainCommanders and leaders Pieter Adriaans...

هذه المقالة قد تتعرض لتغيرات كبيرة وسريعة لأن موضوعها توفي حديثًا. لذلك فإن المعلومات عن الوفاة والأحداث المرتبطة قد تتغير تغيرًا ملحوظًا. التقارير الإخبارية الأولية قد تكون غير موثوقة. التحديثات الأخيرة لهذه المقالة ربما لا تعكس أحدث المعلومات حول الحدث. لا تتردد في تحسي...
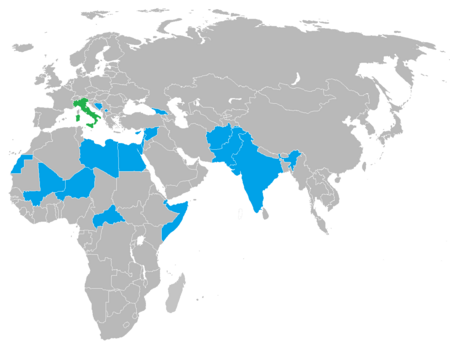
Angkatan Bersenjata ItaliaForze armate italiane (FF.AA.)Lambang Angkatan Bersenjata ItaliaDidirikan4 Mei 1861; 162 Tahun LaluAngkatanAngkatan Darat ItaliaAngkatan Laut ItaliaAngkatan Udara ItaliaCarabinieriMarkas besarRoma, ItaliaKepemimpinanPresiden Republik Sergio MattarellaPerdana Menteri Mario DraghiMenteri Pertahanan Lorenzo GueriniKekuatan personelPersonel aktif165.500 (2019)Personel cadangan18.300 (2019)BelanjaAnggaranUS$28,9 miliar (2020)[1]Persentase terhadap PDB1,6% (2020)&#...

Ravières Vue de l'église de Ravières. Administration Pays France Région Bourgogne-Franche-Comté Département Yonne Arrondissement Avallon Intercommunalité Communauté de communes Le Tonnerrois en Bourgogne Maire Mandat Bruno Letienne 2020-2026 Code postal 89390 Code commune 89321 Démographie Populationmunicipale 719 hab. (2021 ) Densité 33 hab./km2 Géographie Coordonnées 47° 44′ 07″ nord, 4° 13′ 43″ est Altitude Min. 179 mMax. ...

Indian pharmaceutical company This article may rely excessively on sources too closely associated with the subject, potentially preventing the article from being verifiable and neutral. Please help improve it by replacing them with more appropriate citations to reliable, independent, third-party sources. (March 2023) (Learn how and when to remove this message) Divi's Laboratories LimitedDivi's Laboratories' logoFormerlyDivi's Research CentreCompany typePublicTraded asBSE: 532488NSE: ...

Indian film actress (born 1969) Not to be confused with Madhubala. MadhooMadhoo at Esha Deol's wedding at ISKCON templeBornPadma Malini (1969-03-26) 26 March 1969 (age 55)Madras (now Chennai), Tamil Nadu, IndiaOther namesMadhubala, Madhu MaliniYears active1991–presentSpouse Anand Shah (m. 1999)Children2RelativesHema Malini (aunt) Madhoo Shah[1] (born Padma Malini; 26 March 1969[2]), also known formerly as Madhubala, is an Indian ...

Single by Rae Sremmurd featuring Travis Scott CloseSingle by Rae Sremmurd featuring Travis Scottfrom the album SR3MM ReleasedApril 18, 2018GenreTrapLength3:13LabelEarDrummersInterscopeSongwriter(s)Khalif BrownAaquil BrownJacques WebsterMichael WilliamsSamuel GloadeProducer(s)Mike Will Made It30 RocRae Sremmurd singles chronology Chanel (2018) Close (2018) Hands On Me (2018) Travis Scott singles chronology Krippy Kush (Travis Scott Remix)(2017) Close(2018) Love Hurts(2018) Music videoC...

Not to be confused with the Spanish political party The Greens-Green Group. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may need to be rewritten to comply with Wikipedia's quality standards. You can help. The talk page may contain suggestions. (October 2017) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Plea...

المسيحية في باكستانصليب أمام المقبرة المسيحية في مدينة كراتشيمناطق الوجود المميزةالبلد باكستان باكستان 4,000,000 (تقديرات 2020)[1] البنجاب 1,699,843 (تقديرات 1998)[2] بلوشستان 312,000 (تقديرات 1998)[2] إقليم السند 294,885 (تقديرات 1998)[2] خيبر بختونخوا 36,668 (ت...

Kebudayaan AndronovoJangkauangeografisStepa EurasiaPeriodeZaman Perunggu AkhirTanggalk. 2000 SM – 1450 SMDidahului olehKebudayaan Barang Kawat, Kebudayaan Sintashta, Kebudayaan OkunevDiikuti olehKebudayaan Karasuk Kebudayaan arkeologis yang terkait dengan migrasi Indo-Iran (berdasarkan EIEC): Kebudayaan Andronovo, Baktria–Margiana, dan Yaz. Kebudayaan Gandhara (atau Swat), Pemakaman H, Timbunan Tembaga, dan Kebudayaan Barang Abu-Abu adalah kandidat kebudayaan yang berhubungan den...

العلاقات النمساوية الغرينادية النمسا غرينادا النمسا غرينادا تعديل مصدري - تعديل العلاقات النمساوية الغرينادية هي العلاقات الثنائية التي تجمع بين النمسا وغرينادا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه الم...

Questa voce o sezione sugli argomenti sculture e Abruzzo non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Guerriero di CapestranoAutoreAninis(?) DataVI secolo a.C. Materialepietra calcarea Dimensioni209×30×104 cm UbicazioneMuseo Archeologico Nazionale d'Abruzzo, Chieti Coordinate42°16′00.01″N 1...

L'Estelada Blava (The Blue Starred Flag), the blue version of the pro-independence flag L'Estelada Vermella (The Red Starred Flag), the red version of the pro-independence flag Wikisource has original text related to this article: Declaration to start the independence process of Catalonia After pro-independence parties won a majority of seats in the Catalan election on 27 September 2015, the Declaration of the Initiation of the Process of Independence of Catalonia (Catalan: Declaració d'ini...

Spanish handball club This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: BM Puerto Sagunto – news · newspapers · books · scholar · JSTOR (March 2024) Fertiberia Puerto SaguntoFull nameClub Balonmano Puerto SaguntoFounded1951ArenaPabellón Municipal, Puerto Sagunto,Valencian Community,SpainCapacit...
French writer and philosopher Michel HenryMichel Henry at the early 1990sBorn10 January 1922Haiphong, French Indochina (present-day Vietnam)Died3 July 2002 (2002-07-04) (aged 80)Albi, FranceAlma materÉcole Normale Supérieure, University of ParisSpouse Anne Pécourt (m. 1958)Era20th-century philosophyRegionWestern philosophySchoolPhenomenologyMaterial phenomenologyMain interestsEthicsPhilosophy of religionNotable ideasPhenomenology of life,materi...

George Lachmann Mosse George Lachmann Mosse, nato Gerhard Lachmann-Mosse (Berlino, 20 settembre 1918 – Madison, 22 gennaio 1999), è stato uno storico tedesco naturalizzato statunitense che si è occupato soprattutto di nazismo[1], ma ha approfondito anche molti altri temi della storia contemporanea, unendo alla prospettiva storica anche quella sociologica e antropologica. Il suo libro La nazionalizzazione delle masse[2] è considerato il «best seller della storiografia del...

American attorney & diplomat (born 1958) For other people with the same name, see David Friedman (disambiguation). David M. FriedmanOfficial portrait, 2017United States Ambassador to IsraelIn officeMay 15, 2017 – January 20, 2021PresidentDonald TrumpPreceded byDan ShapiroSucceeded byThomas R. Nides Personal detailsBornDavid Melech Friedman (1958-08-08) August 8, 1958 (age 65)Political partyRepublicanSpouse Tammy Sand (m. 1981)Children5Educati...


















































