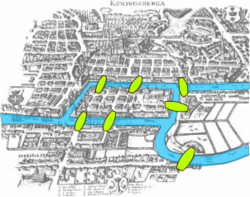
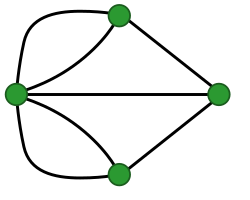
Explanatory indispensability argumentThe explanatory indispensability argument[a] is an argument in the philosophy of mathematics for the existence of mathematical objects. It claims that rationally we should believe in mathematical objects such as numbers because they are indispensable to scientific explanations of empirical phenomena. An altered form of the Quine–Putnam indispensability argument, it differs from that argument in its increased focus on specific explanations instead of whole theories and in its shift towards inference to the best explanation as a justification for belief in mathematical objects rather than confirmational holism. Specific explanations proposed as examples of mathematical explanations in science include why periodical cicadas have prime-numbered life cycles, why bee honeycomb has a hexagonal structure, and the solution to the Seven Bridges of Königsberg problem. Objections to the argument include the idea that mathematics is only used as a representational device, even when it features in scientific explanations; that mathematics does not need to be true to be explanatory because it could be a useful fiction; and that the argument is circular and so begs the question in favour of mathematical objects. BackgroundThe explanatory indispensability argument is an altered form of the Quine–Putnam indispensability argument[3] first raised by W. V. Quine and Hilary Putnam in the 1960s and 1970s.[4] The Quine–Putnam indispensability argument supports the conclusion that mathematical objects exist with the idea that mathematics is indispensable to the best scientific theories.[5] It relies on the view, called confirmational holism, that scientific theories are confirmed as wholes, and that the confirmations of science extend to the mathematics it makes use of.[6] The reliance of the Quine–Putnam argument on confirmational holism is controversial, and it has faced influential challenges from Penelope Maddy and Elliott Sober.[7] The argument has also been criticized for failing to specify the way in which mathematics is indispensable to science; according to Joseph Melia, one would only need to believe in mathematics if it is indispensable in the right way.[8] Specifically, it needs to be indispensable to scientific explanations for it to be as strongly justified as theoretical entities such as electrons.[9] This claim by Melia arose through a debate with Mark Colyvan in the early 2000s over the argument,[b] with Colyvan claiming that mathematics enhances the explanatory power of science. Inspired by this debate, Alan Baker developed an explicitly explanatory form of the indispensability argument, which he termed the enhanced indispensability argument.[c][10] He was also motivated by the objections against confirmational holism; his formulation aimed to replace confirmational holism with an inference to the best explanation.[11] As such, it is more focused on individual scientific explanations than whole theories.[12] Among Baker's influences was Hartry Field, who has been credited with being the first person to draw a connection between indispensability arguments and explanation.[13][d] Baker cited Field as originating an explanatory form of the argument,[15] although Sorin Bangu states that Field merely alluded to such an argument without fully developing it,[16] and Russell Marcus argues he was discussing explanation within the context of the original Quine–Putnam indispensability argument rather than suggesting a new explanatory indispensability argument.[17] According to Marcus, Colyvan's discussion of explanatory power was also initially restricted to its role within the Quine–Putnam indispensability argument. He credits Baker with originating the explanatory indispensability argument.[18] Others, such as Christopher Pincock, place the beginning of the argument's development with Colyvan while noting that Baker sharpened its explanatory focus.[19] Overview of the argumentA standard formulation of the explanatory indispensability argument is given as follows:[20]
The argument is premised on the idea that inference to the best explanation, which is often used to justify theoretical entities such as electrons, can provide a similar kind of support for mathematical objects.[21] It also requires that there are genuinely mathematical explanations in science. For explanations to be genuinely mathematical, it is not enough that they are expressed with the help of mathematics. Instead, mathematics must play an essential part in the explanatory work.[22] Given the argument's reliance on the existence of such explanations, much of the discussion on it has focused on evaluating specific case studies to assess if they are genuine mathematical explanations or not.[23] Case studiesPeriodical cicadas The most influential case study is the example of periodical cicadas provided by Baker.[24] Periodical cicadas are a type of insect that usually have life cycles of 13 or 17 years. It is hypothesized that this is an evolutionary advantage because 13 and 17 are prime numbers. Because prime numbers have no non-trivial factors, this means it is less likely that periodic predators and other competing species of cicada can synchronize with periodic cicadas' life cycles.[25] Baker argues that this is an explanation in which mathematics, specifically number theory, plays a key role in explaining an empirical phenomenon.[26] A number of non-mathematical explanations have been proposed for the length of periodical cicadas' life cycles. For example, a prominent alternative explanation claims that prime-numbered life cycles could have emerged from non-prime life cycles due to developmental delays. This hypothesis is supported by the fact that there are many other species of cicada that have non-prime life cycles, and that developmental changes with 4-year periods have often been observed in periodical cicadas.[27] Some philosophers have also argued that the concept of primeness in the case study by Baker can be replaced with a non-numeric concept of "intersection-minimizing periods", although Baker has argued that this would reduce the generality and depth of the explanation.[28] Others, such as Chris Daly and Simon Langford, argue that using years as a unit of measurement rather than months or seasons is arbitrary; Baker and Colyvan argue that years are an appropriate unit of time for biological development and are the unit used by biologists.[29] The case study has also been criticized for assuming that periodical cicadas have had predators with periodic life cycles in their evolutionary history.[30] Baker has responded to this worry by arguing that it would be impossible to provide direct evidence that periodical cicadas have had periodic predators because "periodicity is not something that can be gleaned from the fossil record".[31] However, he has attempted to make the claim more plausible by arguing that ecological constraints could have restricted the range of the cicadas' possible life cycles, lessening the requirements on periodic predators for the case study to remain mathematically sound.[32] This problem can also be avoided by focusing on other ways in which the prime life cycles could be explanatorily relevant, such as avoidance of competing species of cicada or periodic migration of predators.[33] Bee honeycombAnother prominent case study suggested by Aidan Lyon and Colyvan concerns the hexagonal structure of bee honeycomb. Lyon and Colyvan contend that the hexagonal structure of bee honeycomb can be explained by the mathematical proof of the honeycomb conjecture, which states that hexagons are the most efficient regular tiling of the plane. The explanation goes that there is an evolutionary pressure for honeybees to conserve wax in the construction of their combs, so the efficiency of the hexagonal grid explains why it is selected for.[34] The explanation based on the honeycomb conjecture is potentially incomplete because the proof is a solution to a tiling problem in two dimensions, and disregards the 3D structure of comb cells.[35] Furthermore, many mathematicians do not see the proof of the honeycomb conjecture as an explanatory proof as it employs concepts outside of geometry to establish a geometrical result,[36] although Baker argues that the proof need not be explanatory for the theorem to feature in genuine explanations in science.[37] It is also controversial amongst philosophers whether the subject matter of geometry is purely mathematical, or whether it concerns physical space and structures, leading them to question if the explanation is truly mathematical.[38] There are also non-mathematical explanations for the honeycomb case study. Darwin believed that the hexagonal shape of bee combs was the result of tightly packed spherical cells being pushed together and pressed into hexagons, with bees fixing breakages with flat surfaces of wax further contributing to a hexagonal shape.[39] More modern presentations hold that the shape of honeycomb is due to the flow of molten wax during the construction process.[40] OthersAnother key example is the Seven Bridges of Königsberg, which concerns the impossibility of crossing each of the historical seven bridges in the Prussian city of Königsberg a single time in a continuous walk around the city.[e] The explanation was found by Leonhard Euler in 1735 when he considered whether such a journey was possible.[41] Euler's solution involved abstracting away from the concrete details of the problem to a mathematical representation in the form of a graph, with nodes representing landmasses and lines representing bridges.[42] He reasoned that for each landmass, unless it is a starting or ending point, there must be a path to both enter and exit it. Therefore, there must be at most two nodes in the graph with an uneven number of lines connected to them for such a journey to be possible. But this is not the case for the graph representing the seven bridges in Königsberg, so it is mathematically impossible to cross all seven without crossing over one of the bridges multiple times.[43] The existence at any particular time of antipodal points on the Earth's surface with equal temperature and pressure has been cited as another example. According to Colyvan, this is explained by the Borsuk–Ulam theorem, which entails that for any physical property that varies continuously across the surface of a sphere, there are antipodal points on that sphere with equal values of that property.[44] In response to this example, Baker has argued that it is a prediction rather than an explanation because antipodal points with equal pressure and temperature have not already been measured.[45] Mary Leng also questions whether it is appropriate to model temperature or pressure as continuous functions across individual points on the Earth's surface.[46][f] Other examples proposed by Colyvan include geometrical explanations for Lorentz contraction and gravitational lensing. Baker and Melia have objected to the geometrical aspects of these explanations, which could be interpreted physically instead of mathematically.[48] Sunflower seeds are produced separated by the golden angle, giving rise to spiral patterns which are the densest possible packing of seeds. A key class of mathematical explanations is solutions to optimization problems, which includes the cicada and bee honeycomb case studies. In these cases, a certain feature is explained by showing that it is mathematically optimal.[49] Such explanations are important in evolutionary biology, as mathematical demonstrations of optimality may help to explain why a given trait has been selected for,[50] but also appear in other areas of science such as physics, engineering and economics.[51] Some examples from evolutionary biology are sunflowers' seeds being arranged in a spiral pattern because it produces the densest packing of seeds,[52] and marine predators engaging in Lévy walks because they minimize the average energy consumption required to find prey.[53][g] A number of case studies draw from dynamical systems. Marc Lange, for example, argues that the fact that double pendulums always have four or more equilibrium configurations can be explained by the configuration space of the system forming the surface of a torus, which must have at least four stationary points.[55] Lyon and Colyvan point to the use of phase spaces and the Poincaré map to explain the behaviour of a Hénon–Heiles system, such as the stability of a star's orbit through a galaxy.[56] Some examples are drawn from outside science. For example, widely discussed cases include the explanation for why 23 strawberries cannot be divided equally amongst three people,[57] why it is impossible to square the circle,[58] and why it is impossible to untie a trefoil knot.[59] However, it is unclear to what extent each of these cases are mathematical explanations of physical facts rather than either purely physical or purely mathematical explanations.[h] ObjectionsThe main response to the explanatory indispensability argument, adopted by philosophers such as Melia, Daly, Langford, and Saatsi, is to deny there are genuinely mathematical explanations of empirical phenomena, instead framing the role of mathematics as representational or indexical.[63] According to this response, if mathematics features in scientific explanations, its role is just to help pick out physical facts instead of contributing to the explanatory power of the explanation.[64] Saatsi, and others including Jonathan Tallant and Davide Rizza, have rephrased case studies such as the periodic cicada example to remove reference to mathematical entities in an attempt to provide the true non-mathematical versions of these explanations.[65] Defenders of the explanatory indispensability argument typically argue that the non-mathematical explanations provided are less general and modally weaker than mathematical explanations. They also argue that such explanations contradict scientific practice because scientists often accept the mathematical explanations as genuine scientific explanations.[66] Others, particularly mathematical fictionalists like Mary Leng and Stephen Yablo, have accepted that mathematics plays a genuinely explanatory role in science but argue it can play this role even if mathematical objects do not exist.[64] They point to the use of idealizations like point masses that are used in scientific explanations but are not viewed as literally real.[67][i] Leng argues that the explanatory power of mathematics can be explained by structural similarities between mathematical theory (viewed fictionally) and features of the real world.[69] Yablo appeals to the expressive power of figurative language, claiming it shows that literally untrue statements can often convey more than literally true statements.[70] Colyvan has challenged these types of responses by arguing that fictional or metaphorical language cannot play a role in genuine explanations: "when some piece of language is delivering an explanation, either that piece of language must be interpreted literally or the non-literal reading of the language in question stands proxy for the real explanation."[71] An objection advanced by Bangu states that the explanatory indispensability argument begs the question because it is circular. Bangu argues that examples like the periodic cicada case aim to explain statements that already contain mathematical content, namely the primeness of the cicadas' life cycles. But an inference to the best explanation assumes that the statement being explained is true, so the inclusion of mathematical concepts such as primeness assumes the truth of the mathematics in question.[72][j] Baker has responded to this objection by arguing that the statements being explained in such case studies can be reformulated to remove reference to mathematical entities, leaving mathematics indispensable only to the explanation itself and not the thing being explained.[74] Notes
ReferencesCitations
Sources
Further reading
|