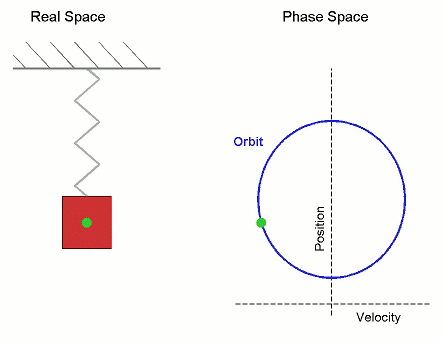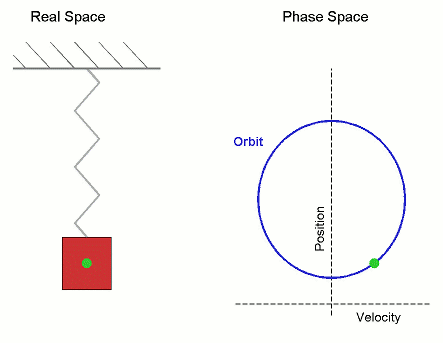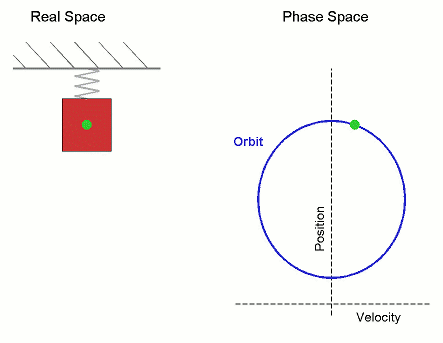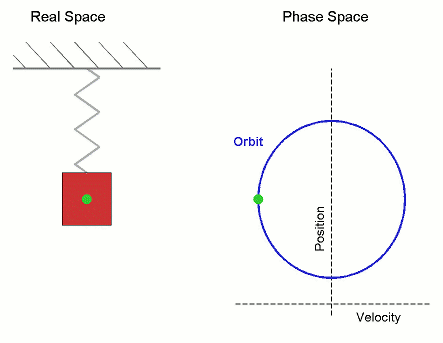
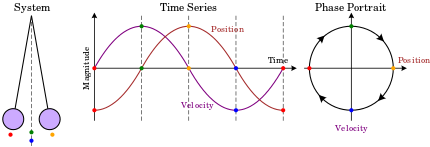
Phase space
|
Read other articles:

2015 turn-based strategy video game 2015 video gameSid Meier's StarshipsDeveloper(s)Firaxis GamesPublisher(s)2KSeriesCivilizationPlatform(s)Microsoft WindowsmacOSiOSReleaseMarch 12, 2015Genre(s)Turn-based strategy Sid Meier's Starships is a turn-based strategy video game developed by Firaxis Games and published by 2K. It was released on March 12, 2015 for Microsoft Windows, OS X, and iOS.[1] The game is a stand-alone title but shares the same universe as Civilization: Beyond Earth, pu...

Herstal Bendera Senjata api FN berukir Herstal (pengucapan bahasa Prancis: [ɛʁstal]; bahasa Wallonia: Hèsta), sebelumnya dinamakan Heristal atau Héristal, adalah sebuah kota madya di Provinsi Liège, Belgia. Terletak di sepanjang sungai Meuse, di wilayah Wallonia. Herstal diaglomerasi ke dalam Liège Raya. Kota madya Herstal mencakup bekas komune Milmort, Vottem, dan sebagian dari Liers (bagian lainnya termasuk ke dalam Juprelle). Pabrik senjata Fabrique Nationale atau biasa dise...

Algoritme Prim adalah sebuah algoritme dalam teori graf untuk mencari pohon rentang minimum untuk sebuah graf berbobot yang saling terhubung. Ini berarti bahwa sebuah himpunan bagian dari edge yang membentuk suatu pohon yang mengandung node, di mana bobot keseluruhan dari semua edge dalam pohon diminimalisasikan. Bila graf tersebut tidak terhubung, maka graf itu hanya memiliki satu pohon rentang minimum untuk satu dari komponen yang terhubung. Algoritme ini ditemukan pada 1930 oleh matematika...

6th SS Mountain Division Nord6. SS-Gebirgs-Division NordLambang divisi (Hagall rune)AktifSeptember 1941 – May 1945Negara Nazi GermanyCabang Waffen-SSTipe unitGebirgsjägerPeranPerang gunungJumlah personelDivisiTokohTokoh berjasaMatthias KleinheisterkampLothar DebesDivisi Gunung SS ke-6 Nord ( bahasa Jerman : 6. SS-Gebirgs-Division Nord) [1] adalah sebuah unit Jerman dari Waffen-SS selama Perang Dunia II, dibentuk pada Februari 1941 sebagai SS Kampfgruppe Nord (Pertempuran ...

J StyleAlbum studio karya Lee Joon-giDirilis17 April 2009GenreDance, popLabelMentor EntertainmentProduserYejeon Media J Style adalah album singel kedua[1] oleh Lee Joon-gi, yang diproduksi dengan musisi Kim Hyung Suk. Album ini terdiri dari 4 baru termasuk 3 lagu dari album sebelumnya My Jun, My Style. Daftar lagu J STYLE Soliloquy (혼잣말) (hon jat mal) I'm Ready Selfless Dedicated Trees (아낌없이 주는나무) (a kkim eops i ju neun na mu) One Word )한마디만) (han ma ...

Elm cultivar Ulmus 'Clusius'Ulmus 'Clusius', Netherlands.GenusUlmusHybrid parentage('Exoniensis' × U. wallichiana) × 'Bea Schwarz' selfedCultivar'Clusius'OriginWageningen, The Netherlands Ulmus 'Clusius' is a Dutch hybrid elm cultivar raised at the Dorschkamp Research Institute for Forestry & Landscape Planning, Wageningen, and released to commerce in 1983. 'Clusius' was derived from a crossing of the same Dutch clones that produced the fastigiate 'Lobel' released in 1973: '202' ('Exoni...

South Korean actress Not to be confused with Lee Hye-young (actress, born 1962). In this Korean name, the family name is Lee. Lee Hye-youngBorn (1971-12-22) December 22, 1971 (age 52)Incheon, South KoreaEducationIncheon City College - Business AdministrationOccupationsActresssingerbusinesswomanYears active1992–presentSpouses Lee Sang-min (m. 2004; div. 2005) unnamed (m. 2011) Korean nameHangul이혜...

UniMás affiliate in El Paso, Texas This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: KTFN – news · newspapers · books · scholar · JSTOR (April 2022) (Learn how and when to remove this template message) KTFNEl Paso, TexasLas Cruces, New MexicoCiudad Juárez, ChihuahuaUnited States–MexicoCityEl Paso, TexasCha...

Main railroad station in Los Angeles, California For other stations with the same name, see Union Station (disambiguation).Los Angeles Union Station The main building with tracks in the backgroundGeneral informationLocation800 North Alameda StreetLos Angeles, CaliforniaUnited StatesCoordinates34°03′19″N 118°14′07″W / 34.05515°N 118.23525°W / 34.05515; -118.23525Owned byLos Angeles County Metropolitan Transportation AuthorityPlatfo...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2016. Kompetisi Sains Madrasah (KSM) adalah sebuah ajang berkompetisi dalam bidang sains yang diselenggarakan oleh Kementerian Agama Republik Indonesia. Kompetisi Sains Madrasah pada awalnya hanya diperuntukkan bagi siswa madrasah (ibtidaiyah, tsanawiyah dan...

زقاق الكوابيسNightmare Alley (بالإنجليزية)Nightmare Alley (بالفرنسية) الشعارمعلومات عامةالصنف الفني فيلم إثارة — فيلم مقتبس من رواية — فيلم دراما المواضيع القائمة ... traveling carnival (en) [1] — مختال[1] — تأثير الثقة المبالغة[1] — knowledge of human nature (en) [1] — التفرس[1] — spiritism (en) &#...

В Википедии есть статьи о других людях с такой фамилией, см. Мидлер. Бетт Мидлерангл. Bette Midler Бетт Мидлер в 2021 году Основная информация Дата рождения 1 декабря 1945(1945-12-01)[1][2][…] (78 лет) Место рождения Гонолулу, США Страна США[3] Профессии актриса, певица �...

Colombian author José Asunción SilvaBornJosé Asunción Silva Gómez(1865-11-27)27 November 1865Bogotá, ColombiaDied23 May 1896(1896-05-23) (aged 30)Bogotá, ColombiaOccupationPoet, author, political figure José Asunción Silva (27 November 1865 in Bogotá – 23 May 1896 in Bogotá) was a Colombian poet. He is considered one of the founders of Latin American Modernismo. Life Born to a wealthy and educated Bogotá family, Asunción Silva led a comfortable life. When he was just ten y...

Perahu gaya pajala Bugis-Makassar berujung ganda dengan tiang tripod dan layar miring persegi (beberapa di antaranya diturunkan dan disimpan di geladak), serta kemudi quarter yang digantung. Gambar ini dibuat tahun 1803 oleh seniman William Westall tentang perahu Bugis di pesisir pantai Arnhem, Australia. Kesempatan itu datang ketika Flinders bertemu dengan armada perahu Bugis yang datang dari Makassar ketika mereka mengumpulkan teripang. Perahu ini memiliki bobot 25 ton dan dipersenjatai den...

Syamsul Mu'arifSyamsul Mu'arif sebagai Menteri Negara Komunikasi dan Informasi Indonesia Menteri Negara Komunikasi dan Informasi Indonesia Ke-1Masa jabatan10 Agustus 2001 – 20 Oktober 2004PresidenMegawati SoekarnoputriWakil PresidenHamzah HazPendahuluJabatan baruPenggantiSofyan DjalilAnggota Dewan Perwakilan Rakyat Republik IndonesiaMasa jabatan1 Oktober 1987 – 10 Agustus 2001PenggantiGusti Iskandar Sukma AlamsyahDaerah pemilihanKalimantan SelatanAnggota Dewan Pe...

Pour les articles homonymes, voir Rodolphe Ier et Rodolphe d'Autriche (homonymie). Rodolphe Ier de Habsbourg Gisant de Rodolphe Ier de Habsbourg, dans la cathédrale de Spire.Titres « Roi des Romains » 23 septembre 1273 – 15 juillet 1291(17 ans, 9 mois et 22 jours) Duc d'Autriche 26 août 1278 – 27 décembre 1282(4 ans, 4 mois et 1 jour) Duc de Carinthie 26 août 1278 – 1er février 1286(7 ans, 5 mois et 6 jours) Biographie Dynas...

Vous lisez un « article de qualité » labellisé en 2012. Six personnalités de l'histoire de la relativité : 1. Isaac Newton 2. James Clerk Maxwell 3. Hendrik Lorentz 4. Henri Poincaré 5. Albert Einstein 6. Hermann Minkowski L’histoire de la relativité restreinte décrit le développement de propositions et constatations empiriques et conceptuelles, au sein de la physique théorique, qui ont permis d’aboutir à une nouvelle compréhension de l’espace et du temps. C...

نادي الأمجاد السعودي تأسس عام 1974 م - 1394 هـ الملعب صبيا السعودية البلد السعودية الدوري دوري الدرجة الثالثة السعودي 2020-2019 2 الإدارة المالك الهيئة العامة للرياضة الطقم الأساسي الطقم الاحتياطي تعديل مصدري - تعديل نادي الأمجاد السعودي هو أحد أندية الدرجة الثالثة بمنط...

International cultural movement active from the 1920s to the 1950s SurrealismThe Treachery of Images, by René Magritte (1929), featuring the declaration Ceci n'est pas une pipe (This is not a pipe)Years active1920s–1950sLocationFrance, BelgiumMajor figuresBreton, Carrington, Dalí, Ernst, Fini, Magritte, OppenheimInfluencesSymbolismAbstract artMetaphysical paintingDadaInfluencedAbstract expressionismFantastic artPostmodern art Part of a series onSurrealism Surrealist Manifesto Surrealist c...

Railway station in Essex, EnglandNot to be confused with Royton railway station or Royston railway station. RoydonGeneral informationLocationRoydon, Epping Forest DistrictEnglandCoordinates51°46′30″N 0°02′10″E / 51.775°N 0.036°E / 51.775; 0.036Grid referenceTL405104Owned byNetwork RailManaged byGreater AngliaPlatforms2Other informationStation codeRYNClassificationDfT category EHistoryOpened1844Passengers2018/19 0.133 million2019/20 0.132 million2020/21 40,7...