4-polytope
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Keuskupan Lucera–TroiaDioecesis Lucerina-TroianaKatolik Katedral LuceraLokasiNegaraItaliaProvinsi gerejawiFoggia-BovinoStatistikLuas1.337 km2 (516 sq mi)Populasi- Total- Katolik(per 2016)67.600 (perkiraan)66,300 (perkiraan) (98.1%)Paroki33Imam55 (diosesan)20 (Ordo Relijius)6 Deakon PermanenInformasiDenominasiGereja KatolikRitusRitus RomaPendirianAbad ke-4 1986 (penggabungan)KatedralKatedral LuceraKonkatedralKatedral TroiaKepemimpinan kiniPausFransiskusUsku...

Pemakaman Muslim Al-Azhar Memorial Garden adalah Taman Pemakaman Islam yang merupakan unit usaha Yayasan Pesantren Islam Al-Azhar[1] yang bergerak di bidang layanan pemakaman Islam sejak tahun 2011.[2] Al-Azhar Memorial Garden : Taman Pemakaman Muslim Pemakaman Muslim Al-Azhar Memorial Garden berlokasi sekitar 10 menit dari exit tol Karawang Timur 2 dan dapat diakses melalui Tol LAYANG Jakarta Cikampek. Pemakaman Islam seluas 25 ha ini dapat menampung sekitar 29,000 jenaz...
Ikon Rusia tentang Pesta Pemuliaan Salib (ikon dari Yaroslavl; karya Gury Nikitin, 1980, Tretyakov Gallery di Moskow). Dalam kalender liturgi Kekristenan, ada beberapa Pesta Pemuliaan Salib Suci yang berbeda, yang mana semuanya memperingati Salib yang digunakan untuk menyalibkan Yesus. Jumat Agung ditujukan untuk mengenang Sengsara dan Penyaliban Kristus, sedangkan Pesta Salib Suci dikhususkan untuk merayakan kayu salib itu sendiri sebagai instrumen keselamatan. 14 September Pesta atau hari r...

У этого термина существуют и другие значения, см. Ворон (значения). Воронангл. The Raven Иллюстрация Джона Нила к сборнику «Ворон и другие стихотворения» (1910) Жанр стихотворение Автор Эдгар Аллан По Язык оригинала английский Дата первой публикации 29 января 1845 Издательство E...

Town in Arizona Town in Arizona, United StatesParker, ArizonaTownHistoric Downtown Parker FlagLocation of Parker in La Paz County, ArizonaParker, ArizonaLocation in the United StatesCoordinates: 34°8′41″N 114°17′23″W / 34.14472°N 114.28972°W / 34.14472; -114.28972[1]CountryUnited StatesStateArizonaCountyLa PazNamed forEly S. ParkerGovernment • MayorKaren Bonds • Vice MayorJerry Hooper • Town CouncilRandy Hartless ...

Марианна Австрийская нем. Maria Anna von Österreich исп. Mariana de Austria Портрет королевы Марианны кисти Веласкеса, 1655-1660 г. Королева Испании 7 октября 1649 — 17 сентября 1665 Предшественник Изабелла Французская Преемник Мария Луиза Орлеанская Регентша Испании 17 сентября 1665 — 6 ноя...

Protected area in New South Wales, AustraliaScottsdale ReserveNew South WalesScottsdale ReserveNearest town or cityBredbo, New South WalesCoordinates35°54′09″S 149°07′41″E / 35.9024°S 149.128°E / -35.9024; 149.128Established2006Area13.28 km2 (5.1 sq mi)Managing authoritiesBush Heritage AustraliaWebsiteScottsdale Reserve Scottsdale Reserve is a 1,328-hectare (3,280-acre) nature reserve on the Murrumbidgee River in south-central New South Wale...

Likia/LykiaLycia (Λυκία)Daerah di Anatolia kunoMakam Lykia yang digali dari batu karang di DalyanLokasiAnatolia selatanNegara adasek. abad ke-15 sampai 14 SM (sebagai Lukka)1250–546 SMBahasaBahasa LikiaIbu kota historisXanthosProvinsi RomawiLyciaLetak Likia di Anatolia Likia atau Lykia (bahasa Likia: Trm̃mis; Yunani: Λυκία) adalah daerah di Anatolia di tempat yang kini menjadi Provinsi Antalya dan Muğla di pesisir selatan Turki. Daerah ini pernah menjadi federasi kota-ko...

Stasiun Semarang TawangBank Jateng BL02KS02KD01JS22 Tampak depan Stasiun Semarang Tawang, 2024Nama lainStasiun TawangLokasiJalan Taman Tawang 1Tanjung Mas, Semarang Utara, Semarang, Jawa Tengah 50174IndonesiaKoordinat6°57′52″S 110°25′40″E / 6.96444°S 110.42778°E / -6.96444; 110.42778Koordinat: 6°57′52″S 110°25′40″E / 6.96444°S 110.42778°E / -6.96444; 110.42778Ketinggian+2 mOperator Kereta Api IndonesiaDaerah Operasi IV S...

American politician James Henry Platt Jr.Member of the U.S. House of Representativesfrom Virginia's 2nd districtIn officeJanuary 27, 1870 – March 3, 1875Preceded byJohn Millson (1861)Succeeded byJohn GoodeChairman of the Committee on Public Buildings and GroundsIn officeMarch 4, 1873 – March 3, 1875Preceded byGeorge Armstrong HalseySucceeded byWilliam Steele Holman Personal detailsBorn(1837-07-13)July 13, 1837Saint John, Colony of New BrunswickDiedAugust 13, 1894(1894...
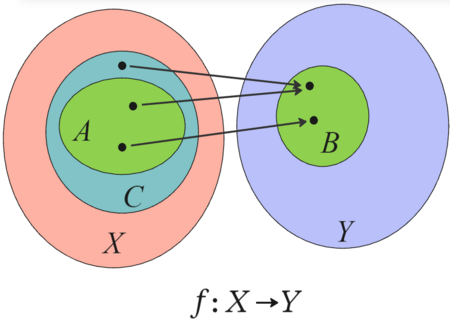
Set of the values of a function For other uses, see Image (disambiguation). f {\displaystyle f} is a function from domain X {\displaystyle X} to codomain Y {\displaystyle Y} . The image of element x {\displaystyle x} is element y {\displaystyle y} . The preimage of element y {\displaystyle y} is the set { x , x ′ {\displaystyle x,x'} }. The preimage of element y ′ {\displaystyle y'} is ∅ {\displaystyle \varnothing } . f {\displaystyle f} is a function from domain X {\disp...

Executive office building of the Government of the Province of Tucumán The Tucumán Government Palace The Tucumán Government Palace is the executive office building of the Government of the Province of Tucumán. Overview Tucumán Province, the most populous and economically important in the Argentine Northwest, lacked architecturally significant government offices, early in the 20th Century. As both a remedy to that absence and a means to encourage urban renewal and development in the provi...

Mizar (Sabotaggio in mare)Dawn Addams e Franco SilvaPaese di produzioneItalia Anno1954 Durata96 min Dati tecnicibianco/nero Genereguerra RegiaFrancesco De Robertis SoggettoFrancesco De Robertis SceneggiaturaFrancesco De Robertis ProduttoreFilm Costellazione FotografiaCarlo Bellero MontaggioEraldo Da Roma MusicheAnnibale Bizzelli ScenografiaGianni Polidori Interpreti e personaggi Dawn Addams: Mizar Paolo Stoppa: console italiano Antonio Centa: dottor Vargas Franco Silva: commendator Luigi Ferr...

Questa voce sull'argomento valli d'Italia è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Valle del LamoneIl Lamone nei pressi di MarradiStati Italia Regioni Emilia-Romagna Toscana Province Ravenna Firenze Località principaliMarradiBrisighella Modifica dati su Wikidata · Manuale La valle del Lamone è un'area geografica definita dal fiume Lamone, che si estende sul territorio delle province di Ravenna in Emilia-Romagna ...

Questa voce sull'argomento calciatori maliani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Cheick Diarra Nazionalità Mali Altezza 174 cm Calcio Ruolo Attaccante Squadra Créteil-Lusitanos CarrieraGiovanili Centre Salif KeitaSquadre di club1 2008-2011 Centre Salif Keita? (?)2011 Stade Malien0 (0)2011-2012 Rennes 220 (17)2011-2013 Rennes19 (1)2013-2014→ I...
周處除三害The Pig, The Snake and The Pigeon正式版海報基本资料导演黃精甫监制李烈黃江豐動作指導洪昰顥编剧黃精甫主演阮經天袁富華陳以文王淨李李仁謝瓊煖配乐盧律銘林孝親林思妤保卜摄影王金城剪辑黃精甫林雍益制片商一種態度電影股份有限公司片长134分鐘产地 臺灣语言國語粵語台語上映及发行上映日期 2023年10月6日 (2023-10-06)(台灣) 2023年11月2日 (2023-11-02)(香�...

Indian film by ShyamaPrasad Ore KadalDirected byShyamaprasadWritten byShyamaprasadProduced byVindhayanStarringMammoottyMeera JasmineNarainRamya KrishnanCinematographyAlagappan N.Edited byVinod SukumaranMusic byOuseppachanRelease date 27 August 2007 (2007-08-27) Running time100 minutesCountryIndiaLanguageMalayalam Ore Kadal (English: The Sea Within) is a 2007 Malayalam-language film written and directed by Shyamaprasad. The film is based on Sunil Gangopadhyay’s Bengali novel H...

Commercial building in Newark-on-Trent, Nottinghamshire, England Corn Exchange, Newark-on-TrentCorn Exchange, Newark-on-TrentLocationCastle Gate, Newark-on-TrentCoordinates53°04′36″N 0°48′47″W / 53.0767°N 0.8130°W / 53.0767; -0.8130Built1847ArchitectHenry DuesburyArchitectural style(s)Italianate style Listed Building – Grade IIOfficial nameFormer Corn Exchange, now Silverline BingoDesignated19 May 1971Reference no.1196050 Shown in Nottinghamshire The...

Muséum des sciences naturelles Liste des musées à Bruxelles (dans les 19 communes de la Région de Bruxelles-Capitale et la périphérie immédiate) triés par nom de commune. Anderlecht Béguinage d'Anderlecht Maison d'Érasme Musée bruxellois de la gueuze Musée d'Anatomie et d'Embryologie humaines Musée de la Médecine Musée national de la Résistance Musée Maurice Carême Auderghem Centre d'Art du Rouge-Cloître Jardin botanique Jean Massart Berchem-Sainte-Agathe Ville de Bruxelles...

Gunung Semanggol adalah sebuah mukim di Daerah Kerian, Negara Bagian Perak, Malaysia. Gunung Semanggol terletak di negeri Perak. Gunung Semanggol, berdekatan dengan Ulu Sepetang dan Kampung Sera. Masjid di Gunung Semanggol Masjid Al-Abrar, Alor Setonggok, 34400 Simpang 4, Perak Masjid Al-Amin, Kampung Selinsing, 34400 Simpang 4, Semanggol, Perak Masjid Al-Ehsaniah, Parit 3, Jalan Gula, 34400 Simpang 4, Semanggol, Perak Masjid Al-Huda, Tebuk Matau, 34400 Simpang 4, Semanggol, Perak Masjid An-N...










































