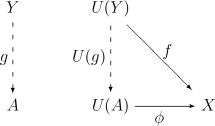Universelle Eigenschaft
|
Read other articles:

Makam Syaikh Ibrahim Ad Dasuqi Ibrahim bin Abdul-Aziz Abul-Majdi (Bahasa Arab: إبراهيم بن عبد العزيز أبو المجد) atau lebih dikenal dengan (إبراهيم الدسوقي) Ibrahim Ad Dasuqi (Dosouk 1255 M / 653 H - 1296 M / 696 H, wafat pada umur 41 tahun) adalah seorang tokoh sufi dan pendiri aliran thariqah Dasuqiyyah atau thariqah Burhamiyyah. Beberapa julukannya adalah Abul Ainain, Syaikhul Islam dan Burhanul Millati Waddin Syaikh Ibrahim Ad Dasuqi adalah “Wali Q...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (فبراير 2016) اتحاد سانت لوسيا لكرة القدم (بالإنجليزية: Saint Lucia Football Association) الرياضة كرة القدم أسس عام 1979 المقر كاست�...

2000 single by Mötley Crüe Hell on High HeelsSingle by Mötley Crüefrom the album New Tattoo Released2000[1]Recorded2000GenreGlam metal, Hard rockLength4:15LabelMötleySongwriter(s)Mick Mars, Vince Neil, Nikki SixxMötley Crüe singles chronology Teaser (1999) Hell on High Heels (2000) New Tattoo (2000) Hell on High Heels is a single by the American heavy metal band Mötley Crüe, released as the first single on their 2000 album New Tattoo. The song charted at number 13 on the Main...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Monkeemania 40 Timeless Hits – news · newspapers · books · scholar · JSTOR (September 2017) (Learn how and when to remove this template message) 1979 greatest hits album by the MonkeesMonkeemania (40 Timeless Hits)Greatest hits album by the Monkees...

العلاقات البوركينابية الفلسطينية فلسطين بوركينا فاسو السفارات لا توجد بعثات دبلوماسية متبادلة الحدود لا حدود برية مشتركة تعديل مصدري - تعديل العلاقات البوركينابية الفلسطينية هي العلاقات الثنائية التي تجمع بين بوركينا فاسو ودولة فلسطين. لا تحتفظ أي م...

Goyang 고양高陽KotaTranskripsi Korea • Hangul고양시 • Hanja高陽市 • Ahli Aksara yang DisempurnakanGoyang-si • McCune-ReischauerKoyang-si Lambang GoyangNegara Korea SelatanWilayahSudogwonPembagian administratif3 gu, 35 dongLuas • Total267,29 km2 (10,320 sq mi)Populasi (2005) • Total1.073.069 • Kepadatan4.014,6/km2 (103,980/sq mi) • DialekSeoul Kota Goyang...

Contoh CAPTCHA CAPTCHA atau Captcha adalah suatu bentuk uji tantangan-tanggapan (challenge-response test) yang digunakan dalam komputasi untuk memastikan bahwa jawaban tidak dihasilkan oleh suatu komputer. Proses ini biasanya melibatkan suatu komputer (server) yang meminta seorang pengguna untuk menyelesaikan suatu uji sederhana yang dapat dihasilkan dan dinilai oleh komputer tersebut. Karena komputer lain tidak dapat memecahkan CAPTCHA, pengguna manapun yang dapat memberikan jawaban yang ben...

1963 single by the Beach BoysSurfer GirlSingle by the Beach Boysfrom the album Surfer Girl B-sideLittle Deuce CoupeReleasedJuly 22, 1963[1]RecordedJune 12, 1963[2]StudioWestern, Hollywood[2]Length2:26LabelCapitolSongwriter(s)Brian WilsonProducer(s)Brian WilsonThe Beach Boys singles chronology Surfin' U.S.A (1963) Surfer Girl (1963) Be True to Your School (1963) Audio samplefilehelp Surfer Girl is a song by American rock band the Beach Boys from their 1963 album Surfer ...

(33342) 1998 WT24PenemuanDitemukan olehLINEARSitus penemuan704Tanggal penemuan1998/11/25Ciri-ciri orbitAphelion1.019Perihelion0.418Sumbu semimayor0.718Eksentrisitas0.418Anomali rata-rata37.5Inklinasi7.3Bujur node menaik82.0Argumen perihelion167.3Ciri-ciri fisikMagnitudo mutlak (H)17.9 (33342) 1998 WT24 adalah sebuah asteroid. Asteroid ini merupakan bagian dari asteroid Aten, yang terletak dekat dengan bumi. Eksentrisitas orbit asteroid ini tercatat sebesar 0.418, seme...

You can help expand this article with text translated from the corresponding article in Japanese. (December 2018) Click [show] for important translation instructions. View a machine-translated version of the Japanese article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English W...

Village in Illinois, United States Village in Illinois, United StatesWestern Springs, IllinoisVillageHistoric water tower logoMotto: A Village of Towering CharacterLocation of Western Springs in Cook County, IllinoisLocation of Illinois in the United StatesCoordinates: 41°48′20″N 87°54′04″W / 41.80556°N 87.90111°W / 41.80556; -87.90111CountryUnited StatesStateIllinoisCountyCookTownshipLyons TownshipFounded1886Government • Village PresidentH...

1633 Ming naval victory over the Dutch East India Company Battle of Liaoluo BayPart of the Sino–Dutch conflictsDateJuly 7 – October 22, 1633LocationLiaoluo Bay, Kinmen (Taiwan Strait)3166 code 24°25′N 118°23′E / 24.41°N 118.38°E / 24.41; 118.38Result Ming victory[1][2]Belligerents Ming dynasty East India CompanyChinese piratesCommanders and leaders Zheng Zhilong Hans Putmans Liu XiangStrength 150 junks[3] 8 warships 50 junks[4 ...

Emblème de la Libye(officieux) Détails Adoption 2021 Supports Passeport Précédentes versions 2011 modifier Les armoiries de la Libye constituent l'emblème héraldique officiel de l'État libyen. Cependant, depuis la guerre civile de 2011 et la chute du régime du colonel Mouammar Kadhafi, le pays ne possède plus d'armoiries officielles. Historique Les premières armoiries officielles sont celles du royaume, adoptées en 1952 et demeurées en vigueur jusqu'à la chute de la monarch...

2016 U.S. presidential election Timeline General election debates Parties Polling national statewide by demographics international Newspaper endorsements primary general Russian interference Russia investigation origins counter-narrative Media coverage Social media International reactions Electors Recounts Faithless electors Vote count Republican Party Primaries Candidates Debates and forums Polling national statewide straw polls Endorsements Results Nominee VP candidate selection Convention ...

Albert Bernhard Frank El autor, a los 42 añosInformación personalNacimiento 17 de enero 1839DresdeFallecimiento 27 de septiembre 1900BerlínResidencia AlemaniaNacionalidad alemánEducaciónEducado en Universidad de Leipzig Información profesionalÁrea biólogo, pteridólogo, micólogo, algólogoEmpleador Universidad de Leipzig Abreviatura en botánica A.B.FrankMiembro de Academia Alemana de las Ciencias Naturales Leopoldina [editar datos en Wikidata] Albert Bernhard Frank ( 17 de...

Catholic catechism for children in the U.S. Baltimore Catechism relief on the Cathedral of Mary Our Queen in Baltimore A Catechism of Christian Doctrine, Prepared and Enjoined by Order of the Third Council of Baltimore, or simply the Baltimore Catechism,[1] was the national Catholic catechism for children in the United States, based on Robert Bellarmine's 1614 Small Catechism. The first such catechism written for Catholics in North America, it was the standard Catholic school text in ...

Shlomo Ben-YosefNative name שלמה בן-יוסףBirth nameSzalom TabacznikBornMay 7, 1913Lutsk, Volhynian Governorate, Russian EmpireDiedJune 29, 1938 (aged 25)Acre Prison, Acre, Mandatory Palestine Cause of deathExecution by hanging AllegianceIrgun Shlomo Ben-Yosef (Hebrew: שלמה בן-יוסף; May 7, 1913 – June 29, 1938) was a member of the Revisionist Zionist underground group Irgun. He is most noted for his participation in an April 21, 1938, attack on a bus carry...

Military campaign against the Ottoman Empire during World War I Battle of Gallipoli redirects here. For other uses, see Battle of Gallipoli (disambiguation). Dardanelles Campaign redirects here. For other uses, see Battle of the Dardanelles. Gallipoli campaignPart of the Middle Eastern theatre of the First World WarA collection of photographs from the campaign. From top and left to right: Ottoman commanders including Mustafa Kemal (fourth from left); Entente warships; V Beach from the deck of...

Swedish cyclist Christofer StevensonStevenson in 2008Personal informationFull nameChristofer StevensonBorn (1982-04-25) 25 April 1982 (age 41)Gothenburg, SwedenTeam informationCurrent teamRetiredDisciplineRoadRoleRiderAmateur teams2004AVC Aix-en-Provence2014Motala AIF CK Professional teams2006Amore & Vita–McDonald's (stagiaire)2007Amore & Vita–McDonald's2008–2009Team GLS–Pakke Shop2010–2011Sparebanken Vest–Ridley2012Team UK Youth2013Concordia Forsikring–Ri...

In this Japanese name, the surname is Kajiwara. Kajiwara Kagetoki (梶原 景時)Japanese Heroes for the Twelve Signs: Boar – Kajiwara Heizo Kagetoki by Utagawa Kuniyoshi (1854)Bornc. 1140Died1200OccupationMilitary leader Kajiwara Kagetoki (梶原 景時, c. 1140[1] – February 6, 1200) was a samurai and retainer of the Kamakura Shogunate during the late Heian and early Kamakura period. He was a spy for Minamoto no Yoritomo in the Genpei War, and a warrior against the T...