–ü—Ä–į–≤–ł–Ľ–Ķ–Ĺ –ľ–Ĺ–ĺ–≥–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ
|
Read other articles:

Katedral Istanbul Katedral Izmir Ini adalah daftar katedral di Turki diurutkan berdasarkan denominasi. Katolik Katedral Gereja Katolik di Turki:[1] Katedral Kabar Sukacita, ńįskenderun (Ritus Latin) Katedral Roh Kudus, Istanbul (Ritus Latin) Katedral Katolik Armenia Santa Maria, Istanbul (Ritus Armenia) Katedral Katolik Yunani Melkit, Istanbul (Ritus Katolik Yunani Melkit) Katedral Santo Yohanes, Izmir (Ritus Latin) Kon-Katedral Santo Antonius dari Padua, Mersin (Ritus Latin) Katedral...

Ini adalah nama Tionghoa; marganya adalah Lee. Ali LeeLahirLee Ka-hingśĚéŚėČť¶®L√©ih GńĀhńęng(Kanton) L«ź JińĀxńęn (Mandarin)27 November 1982 (umur 41)Templat:Hong Kong BritaniaPekerjaanAktris, presenter televisTahun aktif2008‚Äďsekarang Ali Lee Hanzi tradisional: śĚéšĹ≥ŤäĮ Hanzi sederhana: śĚéšĹ≥ŤäĮ Alih aksara Mandarin - Hanyu Pinyin: L«ź JińĀxńęn Yue (Kantonis) - Romanisasi Yale: L√©ih GńĀaisńĀm - Jyutping: Lei5 Gaai1sam1 In 2011 Ali Lee Kai-sum (lahir 27 Desember 1982) adalah se...

Town in Khanty-Mansi Autonomous Okrug, RussiaKhanty-Mansiysk –•–į–Ĺ—ā—č-–ú–į–Ĺ—Ā–ł–Ļ—Ā–ļTown[1] From top down, left to right: Church of the Resurrection, Boris Losev Park, Khanty-Mansiysk Airport,Khanty-Mansiysk Biathlone Center, Archaeopark FlagCoat of armsLocation of Khanty-Mansiysk Khanty-MansiyskLocation of Khanty-MansiyskShow map of RussiaKhanty-MansiyskKhanty-Mansiysk (Khanty‚ÄďMansi Autonomous Okrug)Show map of Khanty‚ÄďMansi Autonomous OkrugCoordinates: 61¬į00‚Ä≤N 69¬į00‚Ä≤E&...

Chemical compound VinyltestosteroneClinical dataOther names17őĪ-Vinyltestosterone; Ethenyltestosterone; 17őĪ-Ethenyltestosterone; 17őĪ-Vinylandrost-4-en-17ő≤-ol-3-one; 17őĪ-Hydroxypregna-4,20-dien-3-oneIdentifiers IUPAC name (8R,9S,10R,13S,14S,17S)-17-Ethenyl-17-hydroxy-10,13-dimethyl-2,6,7,8,9,11,12,14,15,16-decahydro-1H-cyclopenta[a]phenanthren-3-one CAS Number1235-98-9 YPubChem CID222286ChemSpider192964UNIISGZ6EUF8MUChemical and physical dataFormulaC21H30O2Molar mass314.469 g¬∑mo...

This article is about the Japanese television station. For the company that owns it, see Mainichi Broadcasting System. You can help expand this article with text translated from the corresponding article in Japanese. (March 2016) Click [show] for important translation instructions. View a machine-translated version of the Japanese article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and ...
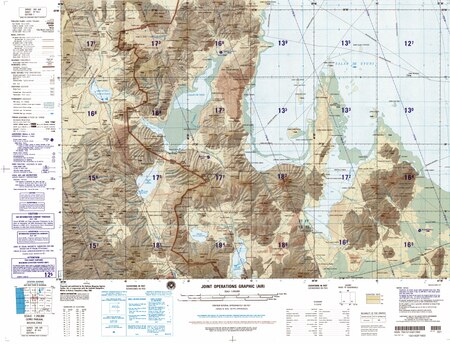
Volcanic complex in Chile Olca volcano lies in the background. 20¬į56‚Ä≤32‚Ä≥S 68¬į30‚Ä≤12‚Ä≥W / 20.94222¬įS 68.50333¬įW / -20.94222; -68.50333[1]Olca-Paruma is a volcanic complex in Chile. Lying on the border between Chile and Bolivia, it is formed by an east‚Äďwest alignment of volcanoes. From west to east, these are Cerro Paruma, Volcan Paruma, Olca, and Mencheca or Michincha. Aside from the mines of Ujina, Rosario, and Quebrada Blanca, the area is sparsely ...

Hospital in California, United StatesSan Joaquin General HospitalSan Joaquin County Health Care ServicesGeographyLocationFrench Camp, San Joaquin County, California, United StatesCoordinates37¬į53‚Ä≤12‚Ä≥N 121¬į16‚Ä≤56‚Ä≥W / 37.8866¬įN 121.2823¬įW / 37.8866; -121.2823OrganizationFundingPublic hospitalTypeTeachingAffiliated universityUniversity of California, DavisUniversity of the PacificServicesEmergency departmentLevel II trauma centerBeds196HelipadYesHistoryOpened18...

ChodkiewiczAlternative name(s)KoŇõciesza odm. ChodkiewiczFamilies1 names Chodkiewicz (ChodŇļkiewicz) DivisionsGmina Gr√≥dek, Gr√≥dek Chodkiewicz (Gryf z Mieczem) is a Polish coat of arms. It was used by the Chodkiewicz family in the times of the Polish‚ÄďLithuanian Commonwealth. A variant of the KoŇõciesza with the Gryf coat of arms and the notable longer family line as well as much bigger family than shown here. Notable bearers Notable bearers of this coat of arms include: Chodkiewicz family...

Belief that the human mind is born with knowledge Part of a series onPhilosophy Philosophy portal Contents Outline Lists Glossary History Categories Disambiguation Philosophies By period Ancient Ancient Egyptian Ancient Greek Medieval Renaissance Modern Contemporary Analytic Continental By region African Egypt Ethiopia South Africa Eastern philosophy Chinese Indian Indonesia Japan Korea Vietnam Indigenous American Aztec philosophy Middle Eastern philosophy Iranian Western American B...

–•—Ä–ł—Ā—ā–ł–į–Ĺ—Ā—ā–≤–ĺ–Ď–ł–Ī–Ľ–ł—Ź –í–Ķ—ā—Ö–ł–Ļ –ó–į–≤–Ķ—ā –Ě–ĺ–≤—č–Ļ –ó–į–≤–Ķ—ā –ē–≤–į–Ĺ–≥–Ķ–Ľ–ł–Ķ –Ē–Ķ—Ā—Ź—ā—Ć –∑–į–Ņ–ĺ–≤–Ķ–ī–Ķ–Ļ –Ě–į–≥–ĺ—Ä–Ĺ–į—Ź –Ņ—Ä–ĺ–Ņ–ĺ–≤–Ķ–ī—Ć –ź–Ņ–ĺ–ļ—Ä–ł—Ą—č –Ď–ĺ–≥, –Ę—Ä–ĺ–ł—Ü–į –Ď–ĺ–≥ –ě—ā–Ķ—Ü –ė–ł—Ā—É—Ā –•—Ä–ł—Ā—ā–ĺ—Ā –°–≤—Ź—ā–ĺ–Ļ –Ē—É—Ö –ė—Ā—ā–ĺ—Ä–ł—Ź —Ö—Ä–ł—Ā—ā–ł–į–Ĺ—Ā—ā–≤–į –ź–Ņ–ĺ—Ā—ā–ĺ–Ľ—č –•—Ä–ĺ–Ĺ–ĺ–Ľ–ĺ–≥–ł—Ź —Ö—Ä–ł—Ā—ā–ł–į–Ĺ—Ā—ā–≤–į –†–į–Ĺ–Ĺ–Ķ–Ķ —Ö—Ä–ł—Ā—ā–ł–į–Ĺ—Ā—ā–≤–ĺ –ď–Ĺ–ĺ—Ā—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ —Ö—Ä–ł—Ā—ā–ł–į–Ĺ—Ā—ā–≤–ĺ –í—Ā–Ķ–Ľ–Ķ–Ĺ—Ā–ļ–ł–Ķ —Ā–ĺ–Ī–ĺ—Ä—č –Ě...

ŔÖōßŔÜŔäō™Ŕąō®ōßŔÖōĻŔĄŔąŔÖōßō™ ōĻōßŔÖō©ōßŔĄō®ōĮōßŔäō© 15 ŔäŔąŔĄŔäŔą 1870 ōßŔĄōßō≥ŔÖ ōßŔĄōĪō≥ŔÖŔä Manitoba (ō®ōßŔĄō•ŔÜō¨ŔĄŔäō≤Ŕäō©) [1]Manitoba (ō®ōßŔĄŔĀōĪŔÜō≥Ŕäō©) ōßŔĄōßō≥ŔÖ ōßŔĄō£ōĶŔĄ Manitoba (ō®ōßŔĄō•ŔÜō¨ŔĄŔäō≤Ŕäō©) ōßŔĄōßō≥ŔÖ ōßŔĄŔÖōģō™ōĶōĪ Man. (ō®ōßŔĄō•ŔÜō¨ŔĄŔäō≤Ŕäō©) Man. (ō®ōßŔĄŔĀōĪŔÜō≥Ŕäō©) ŔÖō™Ŕąō≥ō∑ ōßŔĄōĻŔÖōĪ ōßŔĄŔÖō™ŔąŔāōĻ 80Ŕę1 ō≥ŔÜō© (2014) ō≥ŔŹŔÖŔźŔĎŔä ō®ōßō≥ŔÖ Lake Manitoba Narrows (en) ōßŔĄŔÜō≥ō®ō© Manitoban (ō®ōßŔĄō•ŔÜō¨ŔĄŔäō≤Ŕäō©) Manitobain (ō®ōßŔĄŔĀōĪŔÜō≥Ŕäō©) M...

Questa voce o sezione sull'argomento elezioni non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Elezioni presidenziali in Cile del 1999 Stato Cile Data 12 dicembre 1999, 16 gennaio 2000 Candidati Ricardo Lagos Joaquín Lavín Partiti PPD UDI Coalizioni Concertación Alianza VotiI turno 3.383.33447,96% 3.352.19247,51% VotiII turno 3.683.1585...

–§–Ķ–ī–Ķ—Ä–į–Ľ—Ć–Ĺ–ĺ–Ķ –į–≥–Ķ–Ĺ—ā—Ā—ā–≤–ĺ –Ņ–ĺ –ī–Ķ–Ľ–į–ľ –°–ĺ–ī—Ä—É–∂–Ķ—Ā—ā–≤–į –Ě–Ķ–∑–į–≤–ł—Ā–ł–ľ—č—Ö –ď–ĺ—Ā—É–ī–į—Ä—Ā—ā–≤, —Ā–ĺ–ĺ—ā–Ķ—á–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ł–ļ–ĺ–≤, –Ņ—Ä–ĺ–∂–ł–≤–į—é—Č–ł—Ö –∑–į —Ä—É–Ī–Ķ–∂–ĺ–ľ, –ł –Ņ–ĺ –ľ–Ķ–∂–ī—É–Ĺ–į—Ä–ĺ–ī–Ĺ–ĺ–ľ—É –≥—É–ľ–į–Ĺ–ł—ā–į—Ä–Ĺ–ĺ–ľ—É —Ā–ĺ—ā—Ä—É–ī–Ĺ–ł—á–Ķ—Ā—ā–≤—É—Ā–ĺ–ļ—Ä–į—Č—Ď–Ĺ–Ĺ–ĺ: –†–ĺ—Ā—Ā–ĺ—ā—Ä—É–ī–Ĺ–ł—á–Ķ—Ā—ā–≤–ĺ –ě–Ī—Č–į—Ź –ł–Ĺ—Ą–ĺ—Ä–ľ–į—Ü–ł—Ź –°—ā—Ä–į–Ĺ–į –†–ĺ—Ā—Ā–ł—Ź –ģ—Ä–ł—Ā–ī–ł–ļ—Ü–ł—Ź –†–ĺ—Ā—Ā–ł—Ź –Ē–į—ā–į —Ā–ĺ–∑–ī–į–Ĺ–ł—Ź 6 —Ā–Ķ–Ĺ—ā—Ź–Ī—Ä—Ź...

ŚúüŚļďśõľśĖĮŚĚ¶śÄĽÁĽüŚúüŚļďśõľśĖĮŚĚ¶ŚõĹŚĺĹŚúüŚļďśõľśĖĮŚĚ¶śÄĽÁĽüśóóÁŹĺšĽĽŤįĘŚįĒŤĺĺŚįĒ¬∑ŚąęŚįĒŚĺ∑Á©ÜŚďąśĘÖŚ§öŚ§ęŤá™2022ŚĻī3śúą19śó•ŚģėťāłťėŅšĽÄŚďąŚ∑īŚĺ∑śÄĽÁĽüŚļúÔľąOguzkhan Presidential PalaceԾȜ©üťóúśČÄŚú®ŚúįťėŅšĽÄŚďąŚ∑īŚĺ∑šĽĽŚĎĹŤÄÖÁõīśé•ťÄČšłĺšĽĽśúü7ŚĻīԾƌŹĮŤŅěťÄČŤŅ욼Ľť¶ĖšĽĽŤź®ŚłēŚįĒÁ©ÜśčČÁČĻ¬∑ŚįľšļöšĹźŚ§ęŤģĺÁęč1991ŚĻī10śúą27śó• ŚúüŚļďśõľśĖĮŚĚ¶ŚúüŚļďśõľśĖĮŚĚ¶śĒŅŚļúšłéśĒŅś≤Ľ ŚõĹŚģ∂śĒŅŚļú ŚúüŚļďśõľśĖĮŚĚ¶Śģ™ś≥ē ŚõĹśóó ŚõĹŚĺĹ ŚõĹś≠Ć Áęčś≥ēś©üťóúÔľąŤčĪŤĮ≠ÔľöNational Council of TurkmenistanÔľČ ...

ŔáōįŔá ōßŔĄŔÖŔāōßŔĄō© ō®ō≠ōßō¨ō© ŔĄŔÖōĪōßō¨ōĻō© ōģō®ŔäōĪ ŔÖōģō™ōĶ ŔĀŔä ŔÖō¨ōßŔĄŔáōß. ŔäōĪō¨ŔČ ŔÖŔÜ ōßŔĄŔÖōģō™ōĶŔäŔÜ ŔĀŔä ŔÖō¨ōßŔĄŔáōß ŔÖōĪōßō¨ōĻō™Ŕáōß Ŕąō™ō∑ŔąŔäōĪŔáōß. ō™ō≠ō™ōßō¨ ŔáōįŔá ōßŔĄŔÖŔāōßŔĄō© ō•ŔĄŔČ ō™ŔÜō≥ŔäŔā ŔĄō™ō™ŔÜōßō≥ō® ŔÖōĻ ōĮŔĄŔäŔĄ ōßŔĄō£ō≥ŔĄŔąō® ŔĀŔä ŔąŔäŔÉŔäō®ŔäōĮŔäōß. ŔĀō∂ŔĄŔčōßōĆ ō≥ōßŔáŔÖ ō®ō™ŔÜō≥ŔäŔāŔáōß ŔąŔĀŔā ōĮŔĄŔäŔĄ ōßŔĄō£ō≥ŔĄŔąō® ōßŔĄŔÖōĻō™ŔÖōĮ ŔĀŔä ŔąŔäŔÉŔäō®ŔäōĮŔäōß. (ō£ŔÉō™Ŕąō®ōĪ 2018) ōįŔÉōßō° ōĶŔÜōßōĻŔäōĶŔÜŔĀ ŔĀōĪōĻŔä ŔÖŔÜ ōĻŔĄŔÖ ōßŔĄō≠ōßō≥Ŕąō®[1] ‚ÄĒ ÔŅĹ...

Former hospital in Battery Point, Tasmania, Australia Hospital in Tasmania, AustraliaQueen Alexandra Hospital, HobartGeographyLocationBattery Point, Hobart, Tasmania, AustraliaOrganisationCare systemDHHSTypeMaternity, neonatal careAffiliated universityNoneServicesEmergency departmentYes, Neonatal Intensive careBeds11HistoryOpened1902Closed1980Links The Queen Alexandra Hospital for Women was a maternity hospital and children's hospital established at Hobart, Tasmania in 1905 to commemorate the...
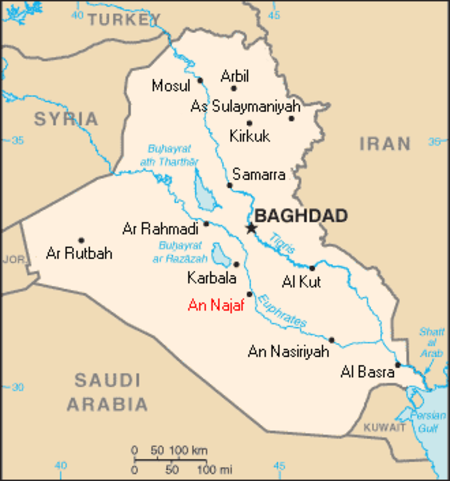
ŔĄŔÖōĻōßŔÜŔć ō£ōģōĪŔČōĆ ō∑ōßŔĄōĻ ōßŔĄŔÜō¨ŔĀ (ō™Ŕąō∂Ŕäō≠). ōßŔĄŔÜō¨ŔĀ ōßŔĄō£ōīōĪŔĀ ōßŔĄŔÜō¨ŔĀ ō∂ōĪŔäō≠ ōßŔĄō•ŔÖōßŔÖ ōĻŔĄŔä ō®ŔÜ ō£ō®Ŕä ō∑ōßŔĄō® ŔĀŔä ōßŔĄŔÜō¨ŔĀ. ōßŔĄŔÜō¨ŔĀōīōĻōßōĪ ōßŔĄŔÜō¨ŔĀ ōģōĪŔäō∑ō© ōßŔĄŔÖŔąŔāōĻ ōßŔĄŔĄŔāō® ŔąōßōĮŔä ōßŔĄō≥ŔĄōßŔÖōĆ ōßŔĄō≠ŔäōĪō©ōĆ ōßŔĄōļōĪŔäōĆ ō®ōßŔÜŔäŔāŔäōß ō™ōßōĪŔäōģ ōßŔĄō™ō£ō≥Ŕäō≥ 661 (ŔÖŔÜōį 1363 ō≥ŔÜō©) ō™Ŕāō≥ŔäŔÖ ō•ōĮōßōĪŔä ōßŔĄō®ŔĄōĮ ōßŔĄōĻōĪōßŔā[1] ōĻōßōĶŔÖō© ŔĄŔÄ ŔÖō≠ōßŔĀōłō© ōßŔĄŔÜō¨ŔĀ ōßŔĄŔÖō≠ōßŔĀōłō© ŔÖō≠...

Disambiguazione ‚Äď Se stai cercando altri significati, vedi Disney Junior (disambigua). Disney JuniorPaese Stati Uniti Linguainglese Tipotematico Targetbambini Data di lancio14 febbraio 2011 (contenitore su Disney Channel) 23 marzo 2012 (canale televisivo) Canale sostituitoPlayhouse Disney GruppoThe Walt Disney Company EditoreDisney Branded Television Sitowww.disneyjunior.com DiffusioneSatelliteDish NetworkCanale 168 (SD) DirecTVCanale 289 (SD/HD) C-BandAMC 11 ‚Äď Canale 44AMC 18 ‚Äď Canale...

Disambiguazione ‚Äď Se stai cercando altri significati, vedi Pieve (disambigua). Abbazia di Sant'Egidio (XI secolo) a Sotto il Monte Giovanni XXIII Pieve di S.Stefano in Candelara, Pesaro Una pieve (dal latino plebs, popolo) √® un luogo di culto cattolico. Con questo termine si indicava nel Medioevo anche una comunit√† di fedeli ed il territorio su cui la pieve esercitava la propria giurisdizione[1]. Nell'Alto Medioevo ad esse erano riservate le funzioni liturgiche pi√Ļ importanti pe...

Dried, split pulses used for cooking Dhal redirects here. For the Arabic letter, see ŠłéńĀl. For other uses, see Dal (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Dal ‚Äď news ¬∑ newspapers ¬∑ books ¬∑ scholar ¬∑ JSTOR (March 2014) (Learn how and when to remove this message) DalLentils are a st...















































