Weaire–Phelan structure
| |||||||
Read other articles:

The Great PassagePoster Jepang Asli.Nama lainJepang舟を編むHepburnFune o Amu SutradaraYuya IshiiProduserTomoo TsuchiiKimitaka GokaFumitsugu IkedaYasuyuki IwanamiDitulis olehKansaku WatanabeBerdasarkanThe Great Passageoleh Shiwon MiuraPemeranRyuhei MatsudaAoi MiyazakiJoe OdagiriKaoru KobayashiGo KatoPenata musikTakashi WatanabeSinematograferJunichi FujisawaPenyuntingShinichi FushimaPerusahaanproduksiFilmmakersLittle More Co.DistributorShochikuTanggal rilis 13 April 2013 (2...

American professor This biography of a living person relies too much on references to primary sources. Please help by adding secondary or tertiary sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately, especially if potentially libelous or harmful.Find sources: Josephine Donovan – news · newspapers · books · scholar · JSTOR (August 2017) (Learn how and when to remove this template message) Jo...

Voce principale: Brescia Calcio. Associazione calcio BresciaStagione 1972-1973 Sport calcio Squadra Brescia Allenatore Giuliano Piovanelli (1ª-19ª) Renato Gei (20ª-38ª) Presidente Oscar Comini Serie B17º Coppa ItaliaPrimo turno Maggiori presenzeCampionato: Inselvini (38) Miglior marcatoreCampionato: Marino (8) StadioStadio Mario Rigamonti 1971-1972 1973-1974 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l'Associazione Calcio Brescia ne...

Airport in Mrčevac, MontenegroTivat AirportAerodrom TivatАеродром ТиватIATA: TIVICAO: LYTVSummaryAirport typePublicOperatorAirports of MontenegroServesTivatLocationMrčevac, MontenegroElevation AMSL20 ft / 6 mCoordinates42°24′17″N 18°43′24″E / 42.40472°N 18.72333°E / 42.40472; 18.72333Websitemontenegroairports.comMapTIVLocation of airport in MontenegroRunways Direction Length Surface ft m 14/32 8,202 2,500 Asphalt Statistics (20...

Artikel ini memberikan informasi dasar tentang topik kesehatan. Informasi dalam artikel ini hanya boleh digunakan untuk penjelasan ilmiah; bukan untuk diagnosis diri dan tidak dapat menggantikan diagnosis medis. Wikipedia tidak memberikan konsultasi medis. Jika Anda perlu bantuan atau hendak berobat, berkonsultasilah dengan tenaga kesehatan profesional. Tinitus adalah telinga berdering, berdesir, atau jenis suara yang tampaknya berasal di telinga atau kepala. Dalam banyak kasus itu bukan masa...

This article is about the town in Albania. For the musician, see Andrew Manze. Municipal unit in Durrës, AlbaniaManëzMunicipal unitStreet in the municipality after the local elections in 2011ManëzCoordinates: 41°26′N 19°35′E / 41.433°N 19.583°E / 41.433; 19.583Country AlbaniaCountyDurrësMunicipalityDurrësPopulation (2011) • Municipal unit6,652Time zoneUTC+1 (CET) • Summer (DST)UTC+2 (CEST)Postal Code2011Area Code(0)572 Man...

American college basketball season 1998–99 North Carolina Tar Heels men's basketballNCAA tournament, Round of 64ConferenceAtlantic Coast ConferenceRankingCoachesNo. 18APNo. 13Record24–10 (10–6 ACC)Head coachBill Guthridge (2nd season)Assistant coaches Phil Ford (11th season) Dave Hanners (9th season) Pat Sullivan (2nd season) Home arenaDean Smith CenterSeasons← 1997–981999–2000 → 1998–99 ACC men's basketball standings vte Conf Overall Team...

ديمقراطيةمعلومات عامةصنف فرعي من نظام سياسي جزء من أنظمة أفلاطون الخمس ممثلة بـ أنواع الديمقراطية لديه جزء أو أجزاء ديمقراطية مباشرةديمقراطية تمثيليةالهيئة الانتخابية النقيض أوتوقراطية تعديل - تعديل مصدري - تعديل ويكي بيانات جزء من سلسلة مقالات حولالديمقراطية تاريخ انت...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2019) مجموعة جيوش الوسط الدولة ألمانيا النازية الإنشاء 1941 الانحلال 1944 جزء من فيرماخت الاشتبا�...

Ghanaian stew Kontomire Stew with eggs and plantain Kontomire stew is a stew made from cocoyam leaves (known in the Akan language as kontomire), commonly prepared in the home and very popular in Ghanaian cuisine.[1] In Ghana, kontomire stew is served with variety of dishes,[2][3] including steamed rice, cooked yam and plantain.[4] Its English designation palava sauce is said to originate from the people of Elmina.[5][6] Ingredients Preparing kon...

Washington State Senate elections, 2018 ← 2016 November 6, 2018 2020 → 25 of 49 seats in the Washington State Senate25 seats needed for a majority Majority party Minority party Leader Karen Keiser Mark Schoesler Party Democratic Republican Leader's seat 33rd-Des Moines 9th-Ritzville Last election 24[a] 25[a] Seats before 25 24 Seats won 28[a] 21[a] Seat change 3 3 Popular vote 982,741 516,476 Pe...

Political party in Greece Drassi ΔράσηLeaderTheodoros SkylakakisGeneral SecretaryMelina DaskalakisSpokespersonPanagiotis MichalopoulosFounderStefanos ManosFounded2009 (2009)Dissolved2019 (2019)Preceded byThe LiberalsMerged intoNew DemocracyHeadquarters98Α, Vasilissis Sofias Avenue, 11528, AthensIdeologyLiberalism[1]PostnationalismDecentralizationEconomic liberalismMeritocracyNeoliberalismPolitical positionCentre to Centre-rightEuropean affiliationAll...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Les Dix Commandements musical – news · newspapers · books · scholar · JSTOR (December 2021) (Learn how and when to remove this message) MusicalLes Dix CommandementsCover of DVD releaseMusicPascal ObispoLyricsLionel Florence and Patrice GuiraoProductionsEli...

Questa voce sull'argomento documenti della Chiesa cattolica è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. La lettera apostolica è un tipo di documento ufficiale redatto dal pontefice della Chiesa cattolica. Si colloca al quinto grado di importanza, al di sotto: della costituzione apostolica; dell'enciclica del motu proprio e dell'esortazione apostolica; ma al di sopra: della lettera semplice; e del ...

Christ healing the paralytic at Capernaum (Yesus menyembuhkan orang lumpuh di Kapernaum) karya Bernhard Rode 1780. Yesus menyembuhkan orang lumpuh adalah suatu peristiwa mukjizat yang diperbuat oleh Yesus Kristus yang dicatat dalam bagian Perjanjian Baru di Alkitab Kristen. Peristiwa ini secara khusus dicatat dalam tiga kitab Injil Sinoptik, yaitu pada Injil Matius pasal 9,[1] Injil Markus pasal 2,[2] dan Injil Lukas pasal 5.[3] Injil Yohanes tidak memuat peristiwa ini...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (August 2010) (Learn how and when to remove this message) Walter Butler of Ballinakill Castle, Roscrea (c. 1600 – 25 December 1634) was a military officer, who served as a colonel (Oberst) in the Imperial Army under Albrecht von Wallenstein and was involved in Wallenstein's assassination in 1634. Ancestry Walte...

Voce principale: Associazione Sportiva Dilettantistica Sangiovannese 1927. Associazione Calcio SangiovanneseStagione 2004-2005Sport calcio Squadra Sangiovannese Allenatore Maurizio Sarri Presidente Arduino Casprini Serie C18º posto nel girone A. Maggiori presenzeCampionato: Stamilla (35) Miglior marcatoreCampionato: Bongiorni (9) 2003-2004 2005-2006 Si invita a seguire il modello di voce Questa pagina raccoglie le informazioni riguardanti l'Associazione Calcio Sangiovannese nelle compe...

Siegel der Gemeinschaft Gedenktafel mit den Namen der Gründer Die Société Notre-Dame de Montréal (vollständiger Name: Société de Notre-Dame de Montréal pour la conversion des Sauvages de la Nouvelle-France, dt. „Gesellschaft Unserer Lieben Frau von Montreal für die Bekehrung der Wilden Neufrankreichs“) war eine religiöse Laiengemeinschaft, die von 1639 bis 1663 existierte. Sie war verantwortlich für die Gründung der Siedlung Ville-Marie in Neufrankreich, aus der sich die kanad...

Gerli PadarGerli Padar représentant l'Estonie lors du Concours Eurovision de la chanson 2007 (demi-finale).BiographieNaissance 6 novembre 1979 (44 ans)HaljalaNationalité estonienneActivité ChanteusePériode d'activité Depuis 1994Fratrie Tanel PadarAutres informationsGenre artistique Popmodifier - modifier le code - modifier Wikidata Gerli Padar (née le 6 novembre 1979 à Haljala, Estonie) est une artiste estonienne. Elle est surtout connue pour son interprétation de la chanson Part...
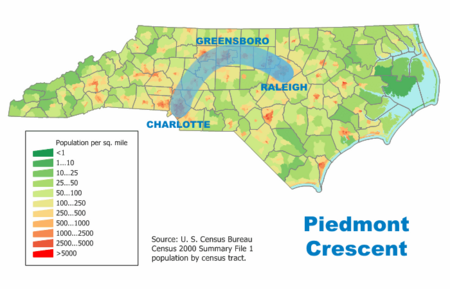
Region in the U.S. state of North Carolina The Piedmont Crescent, also known as the Piedmont Urban Crescent, is a large, polycentric urbanized region in the U.S. state of North Carolina that forms the northern section of the rapidly developing Piedmont Atlantic megalopolis (or megaregion), a conurbation also known as the I-85 Boombelt, which extends from the Raleigh area in North Carolina, southwards to Atlanta, Georgia in the southeastern United States.[1] The region includes seven o...









