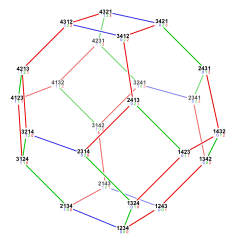
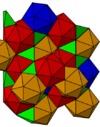
Bitruncated cubic honeycomb
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Pour les articles ayant des titres homophones, voir Gray's Anatomy (homonymie). Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (août 2023). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et r...

Dinas PengadaanTentara Nasional Indonesia Angkatan DaratDibentuk21 April 2020Negara IndonesiaCabang TNI Angkatan DaratBagian dariTentara Nasional IndonesiaJulukanDisadaadTokohKomandan saat iniBrigadir Jenderal TNI Hari Pahlwantoro Dinas Pengadaan Angkatan Darat, atau disingkat Disadaad adalah sebuah organisasi yang diresmikan oleh Kepala Staf Angkatan Darat Jenderal TNI Andika Perkasa pada tanggal 21 April 2020. Pembentukan Dinas Pengadaan Angkatan Darat ini sesuai dengan amanah Peratura...

Disambiguazione – Se stai cercando altri significati, vedi Longobardi (disambigua). Disambiguazione – Longobarda rimanda qui. Se stai cercando altri significati, vedi Longobarda (disambigua). Fonte battesimale del patriarca Callisto, 730-740, situato a Cividale del Friuli, presso il Museo diocesano cristiano e del tesoro del duomo. I Longobardi furono una popolazione germanica, protagonista tra il II e il VI secolo di una lunga migrazione che la portò dal basso corso dell'Elba f...

Surah ke-51az-Zariyat Angin Yang MenerbangkanTeks ArabTerjemahan KemenagKlasifikasiMakkiyahJuzJuz 26 (ayat 1-30) Juz 27 (ayat 31-60)Jumlah ruku3 rukuJumlah ayat60 ayat Surah Az-Zariyat (Arab: الذاريات,Angin Yang Menerbangkan) adalah surah ke-51 dalam al-Qur'an. Surah ini tergolong surah Makkiyah yang terdiri atas 60 ayat. Dinamakan Az-Zariyat yang berarti Angin Yang Menerbangkan diambil dari perkataan Az-Zariyat yang terdapat pada ayat pertama surah ini. Terjemahan Dengan nama Allah Y...

SMA Negeri 46 JakartaInformasiDidirikan10 Januari 1977 (sebagai filial dari SMA Negeri 18 Jakarta)JenisNegeriAkreditasiAKepala SekolahAchmad Safari, S.Pd., M.Si.Ketua KomiteNonie Indrayanto, S.T.Jurusan atau peminatanMIPA dan IPSRentang kelasX, XI, XII MIPA, XII IPSKurikulumKurikulum Merdeka dan Kurikulum 2013Jumlah siswa972AlamatLokasiJalan Masjid Darussalam Kav. 23-25, Blok-A, Gandaria Utara, Kebayoran Baru, Jakarta Selatan, DKI Jakarta, IndonesiaTel./Faks.021-7246695Koordina...

City in North Karnataka, India This article is about the City. For its eponymous district, see Bidar district. For Taluka (Tehsil), see Bidar taluk. See also: Bidar (disambiguation) This article possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (February 2016) (Learn how and when to remove this message) City in KarnatakaBidarCity(clockwise from top) Bidar Fort; One...

American government official and business advocate (born 1970) Isabel Guzman27th Administrator of the Small Business AdministrationIncumbentAssumed office March 17, 2021PresidentJoe BidenDeputyDilawar SyedPreceded byJovita Carranza Personal detailsBorn1970 or 1971 (age 53–54)[1]Burbank, California, U.S.EducationUniversity of Pennsylvania (BS) Isabella Casillas Guzman[2] (born 1970) is an American government official serving as the administrator of the Sm...

List of historic UK ships and vessels Registered vessel flagMembership of the National Historic Fleet flagFlags of the National Register of Historic Vessels The National Historic Fleet is a list of historic ships and vessels located in the United Kingdom, under the National Historic Ships register. National Historic Ships UK is an advisory body which advises the Secretary of State for Culture, Media and Sport and other public bodies on ship preservation and funding priorities. As part of this...

Zoo in Tupelo, Mississippi, United States Tupelo Buffalo Park and ZooA large herd of buffalo roam the park.34°17′13″N 88°46′07″W / 34.2869°N 88.7687°W / 34.2869; -88.7687Date opened2001; 23 years ago (2001)[1]LocationTupelo, Mississippi, United StatesLand area210 acres (0.85 km2)[2]No. of animals450No. of species125OwnerDan and Shelia Franklin[1]Websitewww.tupelobuffalopark.com The Tupelo Buffalo Park and Zoo i...

الدوري الإسكتلندي الدرجة الأولى 2018–19 تفاصيل الموسم البطولة الإسكتلندية النسخة 113 البلد المملكة المتحدة التاريخ بداية:4 أغسطس 2018 نهاية:4 مايو 2019 المنظم الدوري الإسكتلندي للمحترفين لكرة القدم البطل نادي روس كاونتي مباريات ملعوبة 180 عدد المشاركين ...

Australian comedian and actor Greg FleetFleet preparing to go on stage at a Melbourne showBirth nameGregory FleetBorn1962 (age 61–62)Michigan, United StatesAlma materGeelong Grammar SchoolYears active1984–presentGenresStand-up comedyWebsiteOfficial site Gregory Fleet is an Australian comedian and actor. History Early life Fleet was born in Michigan, in the United States. His father moved the family to Australia when Greg was four. He grew up in Geelong, and as a teenage...

Methodist university in Sioux City, Iowa, US For the college of the Chinese University of Hong Kong, see Morningside College. Morningside UniversityFormer namesMorningside College (1894–2021)TypePrivate universityEstablishedDecember 5, 1894; 129 years ago (1894-12-05)Religious affiliationUnited Methodist ChurchEndowment$60 million (2020)[1]PresidentAlbert D. MosleyAcademic staff250Total staff250Students2,400LocationSioux City, Iowa, United States43° 31′ 36.7″ ...

Questa voce sull'argomento missioni spaziali è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. STS-36Emblema missione Dati della missioneOperatoreNASA NSSDC ID1990-019A SCN20512 ShuttleAtlantis Lancio28 febbraio 1990, 2:50:22 a.m. EST Luogo lancioRampa 39A Atterraggio4 marzo 1990, 10:08:44 a.m. PST Sito atterraggioEdwards Air Force Base (pista 23) Durata4 giorni, 10 ore, 18 minuti e 22 secondi Proprietà...

Wrigley Field Wrigley Field 2018.Tidigare namnWeeghman Park (1914–1920)Cubs Park (1920–1926)SmeknamnThe Friendly Confines[1]Plats1060 West Addison Street[1], Chicago, IL, USATypBasebollarenaKapacitet41 649[2]ÄgareChicago CubsUnderhållChicago CubsByggkostnad250 000 dollarArkitektZachary Taylor Davis[3]EntreprenörBlome-Sinek Company[3]PlanstorlekLeft field: 108 m (355 fot)Center field: 122 m (400 fot)Right field: 108 m (353 fot)UnderlagGräsHemmalagChicago Whales (MLB) (1...

Para otros usos de este término, véase Sopa (desambiguación). El gazpacho es una sopa fría Tarator Una sopa fría es una preparación culinaria que, siendo de textura líquida o cremosa, se sirve a temperatura inferior a la temperatura ambiente.[1] Muchas veces, se elabora principalmente a base de hortalizas. De esta forma, diversas cocinas del mundo poseen recetas de sopas frías, como puede ser la española con el gazpacho, el ajoblanco y el salmorejo, y la francesa con la vichy...

Legg Mason Tennis Classic 2008Sport Tennis Data9 agosto – 17 agosto Edizione40a SuperficieCemento CampioniSingolare Juan Martín del Potro Doppio Marc Gicquel / Robert Lindstedt 2007 2009 Juan Martín del Potro vincitore del singolare maschile Il Legg Mason Tennis Classic 2008 è stato un torneo di tennis giocato sul cemento È stata la 40ª edizione del Legg Mason Tennis Classic, che fa parte della categoria International Series nell'ambito dell'ATP Tour 2008. Si è giocato al William H.G....

Per popoli indigeni o aborigeni o nativi oppure autoctoni (dal latino indigena, composto di inde, ivi, e -geno, nato, corrispondente latineggiante del lemma autoctono) si intendono quelle popolazioni le cui origini della presenza, in un particolare territorio, risalgono alla preistoria. Indigeni Palikur che eseguono canti tradizionali durante una cerimonia nell'agosto 2019. Indice 1 Terminologia 2 Storia 3 Nativismo 4 Note 5 Voci correlate 6 Altri progetti 7 Collegamenti esterni Terminologia ...

American self-publishing company iUniverseParent companyAuthor SolutionsFounded1999Country of originUnited StatesHeadquarters locationBloomington, IndianaPublication typesBooksImprintsWriters Club PressOfficial websiteiuniverse.com iUniverse, founded in October 1999, is an American self-publishing company based in Bloomington, Indiana.[1] It has been owned by Author Solutions since 2008 (which has been owned by Najafi Companies since 2015). History iUniverse focuses on print-on-demand...

جهة مراكش آسفي علم الإحداثيات 31°22′38″N 8°16′42″W / 31.377089°N 8.278198°W / 31.377089; -8.278198 [1] تاريخ التأسيس 2015 سبب التسمية مراكش، وآسفي تقسيم إداري البلد المغرب التقسيم الأعلى المغرب العاصمة مراكش[2] التقسيمات الإدارية عمالة مرا�...

Voce principale: Reggina Calcio. Reggina CalcioStagione 1999-2000 Sport calcio Squadra Reggina Allenatore Franco Colomba Presidente Pasquale Foti Serie A11º Coppa ItaliaSecondo turno Maggiori presenzeCampionato: Stovini (34) Miglior marcatoreCampionato: Kallon (11)Totale: Kallon (14) StadioOreste Granillo Abbonati24 671 Maggior numero di spettatori27 272 vs Inter Minor numero di spettatori21 051 vs Cagliari Media spettatori22 744 1998-1999 2000-2001 Si invita a segu...