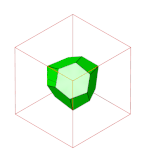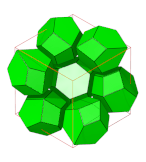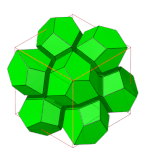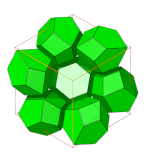
Honeycomb (geometry)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Electronic game of memory skill This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Simon game – news · newspapers · books · scholar · JSTOR (January 2009...

Oriole Park at Camden YardsMaryland has a number of major and minor professional sports franchises. Two National Football League teams play in Maryland, the Baltimore Ravens in Baltimore and the Washington Commanders in Prince George's County. The Baltimore Orioles compete as Major League Baseball franchise in Baltimore. Other professional sports franchises in the state include five affiliated minor league baseball teams, one independent league baseball team, the Baltimore Blast indoor soccer...

Kypello Kyprou 1994-1995 Competizione Coppa di Cipro Sport Calcio Edizione 53ª Organizzatore CFA Date dal 2 novembre 1994al 27 maggio 1995 Luogo Cipro Partecipanti 8 Risultati Vincitore APOEL(14º titolo) Secondo Apollōn Limassol Semi-finalisti OmoniaEN Paralimni Statistiche Incontri disputati 13 Gol segnati 34 (2,62 per incontro) Cronologia della competizione 1993-1994 1995-1996 Manuale La Kypello Kyprou 1994-1995 fu la 53ª edizione della coppa nazionale cipriota. Vide...

KalitengahDesaLokasi Desa KalitengahPeta lokasi Desa KalitengahNegara IndonesiaProvinsiJawa TengahKabupatenBanjarnegaraKecamatanPurwanegaraKode Kemendagri33.04.04.2001 Luas-Kepadatan- Kalitengah adalah desa di kecamatan Purwanegara, Banjarnegara, Jawa Tengah, Indonesia. Pranala luar (Indonesia) Keputusan Menteri Dalam Negeri Nomor 050-145 Tahun 2022 tentang Pemberian dan Pemutakhiran Kode, Data Wilayah Administrasi Pemerintahan, dan Pulau tahun 2021 (Indonesia) Peraturan Menteri Dalam Ne...

English local election This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 1994 Harlow District Council election – news · newspapers · books · scholar · JSTOR (October 2019) (Learn how and when to remove this message) 1994 Harlow District Council election[1][2] ← 1992 5 May 1994 1995&#...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

Capital city of New South Wales, Australia This article is about the Australian metropolis. For the local government area, see City of Sydney. For other uses, see Sydney (disambiguation). SydneyNew South WalesSydney Opera House and Harbour BridgeQueen Victoria BuildingUniversity of SydneyBondi BeachArchibald Fountain and St Mary’s CathedralSydney CBD skylineMap of the Sydney metropolitan areaSydneyCoordinates33°52′04″S 151°12′36″E / 33.86778°S 151.21000°E...

VesterbygaardGeneral informationLocationVesterbygårdvej 20 4490 Jerslev SjællandCountryDenmarkCoordinates55°36′36.7″N 11°16′35.9″E / 55.610194°N 11.276639°E / 55.610194; 11.276639Construction started1840sClientC. A. Fonnesbech Vesterbygaard is a manor house and estate situated north of Tissø, Kalundborg Municipality, some 70 km west of Copenhagen, Denmark. The three-winged main building was constructed for Christen Andreas Fonnesbech in the 1840s. T...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Kaori SakamotoSakamoto pada tahun 2018Informasi PribadiMewakili negara JepangLahir9 April 2000 (umur 24)Kobe, JepangDaerah asalKobe, JepangTempat tinggalKobe, JepangPelatihSonoko Nakano Mitsuko Graham Sei KawaharaKoreograferBenoît RichaudMa...

Ne doit pas être confondu avec Rose des sables (pâtisserie). Pour les articles homonymes, voir Rose des sables (homonymie). Cet article est une ébauche concernant la géologie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Rose des sables Rose des sables (gypse), sud de la Tunisie, 47 x 33 cm. Données clés Catégorie Évaporite Minéraux accessoires Barytine Couleur blanc beige rose Dureté 2 modifier La ...

British Army officer Not to be confused with Peter Labilliere. Sir Peter de la BillièreGeneral Sir Peter de la BilliereBorn (1934-04-29) 29 April 1934 (age 90)Plymouth, Devon, EnglandAllegianceUnited KingdomService/branchBritish ArmyYears of service1952–1992RankGeneralService number424859Commands heldBritish Forces Middle East (1990–91)South East District (1988–90)Headquarters Wales (1985–87)Director Special Forces (1979–83)22 SAS Regiment (1972–74)Battles/warsKorean Wa...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: TÜBİTAK Space Technologies Research Institute – news · newspapers · books · scholar · JSTOR (February 2015) (Learn how and when to remove this message) TÜBİTAK Space Technologies Research InstituteTÜBİTAK Uzay Teknolojileri Araştırma EnstitüsüAbbrevia...

Brazilian footballer (1940–2022) Pele and O Rei redirect here. For the Hawaiian goddess, see Pele (deity). For the Portuguese footballer with the same nickname, see Eusébio. For other uses, see Pele (disambiguation). In this Portuguese name, the first or maternal family name is Arantes and the second or paternal family name is Nascimento. PeléPelé with Brazil in 1970BornEdson Arantes do Nascimento(1940-10-23)23 October 1940[note 1]Três Corações, BrazilDied29 December ...

Governo Rutte IIIIl Primo ministro Mark Rutte nel 2017. Stato Paesi Bassi Ministro-PresidenteMark Rutte(VVD) CoalizioneVVD, D66, CU, CDA Giuramento26 ottobre 2017 Dimissioni15 gennaio 2021 Governo successivo10 gennaio 2022 Rutte II Rutte IV Il Governo Rutte III (in lingua nederlandese: Kabinet-Rutte III) è stato il settantesimo Governo dei Paesi Bassi, in carica per un totale di 4 anni, 2 mesi e 14 giorni, dal 26 ottobre 2017 al 10 gennaio 2022 (sebbene dimissionario a partire dal 15 ge...

Australian politician For other people named Thomas Paterson, see Thomas Paterson (disambiguation). The HonourableThomas PatersonDeputy Leader of the Country PartyIn office19 November 1929 – 27 November 1937LeaderEarle PagePreceded byWilliam GibsonSucceeded byHarold ThorbyMinister for the InteriorIn office9 November 1934 – 29 November 1937Prime MinisterJoseph LyonsPreceded byEric HarrisonSucceeded byJohn McEwenMinister for Markets and TransportIn office10 December 1928&#...

Questa voce o sezione sull'argomento geografia contiene errori ortografici o sintattici oppure è scritta in una forma migliorabile. Commento: voci da evidente traduzione non sempre chiara e comprensibile Contribuisci a correggerla secondo le convenzioni della lingua italiana e del manuale di stile di Wikipedia. Segui i suggerimenti del progetto di riferimento. Transnistria (dettagli) (dettagli) Transnistria - Localizzazione Territorio a status contesoMotivo del contenziosoRepubblica au...

ルサイル・スタジアムLusail Stadiumاستاد لوسيلルサイル・アイコニック・スタジアムLusail Iconic Stadium 2022 FIFAワールドカップでのスタジアム 施設情報所在地 カタール ルサイル起工 2017年4月11日開場 2021年11月21日所有者 カタールサッカー協会グラウンド 天然芝設計者 Foster + Partners POPULOUS建設者 HBK Contracting 中国鉄建[1]使用チーム、大会 サッカーカタール代表2022 FIF...

Dăržavno părvenstvo po futbol 1931 Competizione Dăržavno părvenstvo po futbol Sport Calcio Edizione 7ª Organizzatore BFS Luogo Bulgaria Partecipanti 12 Risultati Vincitore Atletik-Slava 23(1º titolo) Secondo Spartak Varna Statistiche Incontri disputati 11 Gol segnati 48 (4,36 per incontro) Cronologia della competizione 1930 1932 Manuale Il Dăržavno părvenstvo po futbol 1931 fu la settima edizione della massima serie del campionato di calcio bulgaro concluso il 13 ...

Queen of England from 1396 to 1399 For other people named Isabella of Valois, see Isabella of Valois (disambiguation). Isabella of ValoisDuchess of OrléansQueen consort of EnglandTenure31 October 1396 – 29 September 1399Coronation8 January 1397Born9 November 1389Paris, FranceDied13 September 1409 (aged 19)Blois, Loir-et-Cher, FranceBurialAbbey of Saint Laumer of Blois; reinterred in the Couvent des Célestins, Paris, FranceSpouse Richard II of England (m. 1396&#...

日本の政治家岩田 宙造いわた ちゅうぞう 生年月日 1875年4月7日出生地 日本・山口県熊毛郡立野村(現・光市)没年月日 (1966-02-22) 1966年2月22日(90歳没)出身校 旧制山口高等学校卒業東京帝国大学法科大学法律学科(英法)卒業称号 法学博士正三位勲一等瑞宝章配偶者 岩田華奈子子女 長男:岩田永俊次男:岩田健次郎 貴族院勅選議員在任期間 1931年12月12日 - 1946年9月30...