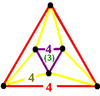
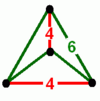
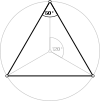
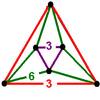
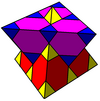
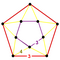
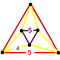
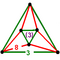
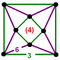
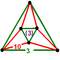
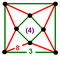
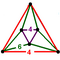
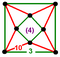
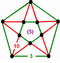
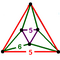
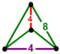
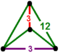
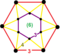
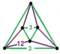
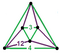
Regular skew apeirohedron
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

You can help expand this article with text translated from the corresponding article in Russian. (January 2022) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do not translate text that appears unreliable or lo...

SMA Negeri 1 Ngawi InformasiDidirikanBerdiri sejak 30 Juli 1980 sebagai SMA Negeri Ngawi berdasarkan No. SK. Pendirian = 0206/O/1980. Berubah nama menjadi SMAN 1 Ngawi pada 24 Agustus 1989 berdasarkan: No. SK. Operasional = 0507/08/1989JenisNegeriAkreditasiA [1] No. SK. Akreditasi = 1347/BAN-SM/SK/2021 Tanggal SK. Akreditasi = 8 Desember 2021Nomor Pokok Sekolah Nasional20508480MotoQualified Dream SchoolKepala SekolahSunarta S.Pd Jurusan atau peminatanIPA dan IPSKurikulumKurikulum...

Historic district in Minnesota, United States United States historic placeNorthrop Mall Historic DistrictU.S. National Register of Historic PlacesU.S. Historic district Northrop Mall facing northShow map of MinnesotaShow map of the United StatesLocationUniversity of Minnesota, Minneapolis, MinnesotaBuilt1910-1971ArchitectCass Gilbert; Clarence H. Johnston Sr.; Morell and Nichols; Roger Martin; Magney, Tusler and Setter; Hammel Green and Abrahamson, Inc., et alArchitectural styleCity Beau...

Bukit SundiKecamatanHamparan Persawahan di Nagari Kinari Bukit SundiNegara IndonesiaProvinsiSumatera BaratKabupatenSolokPemerintahan • Camat-Populasi • Total- jiwaKode Kemendagri13.02.08 Kode BPS1303090 Luas- km²Nagari/kelurahan5 Bukit Sundi (ditulis juga sebagai Bukik Sundi) adalah sebuah kecamatan di Kabupaten Solok, Sumatera Barat, Indonesia. Kecamatan ini berjarak sekitar 33 kilometer berkendara dari ibukota kabupaten Solok ke arah utara atau 8 kilometer teng...

Cet article est une ébauche concernant l’automobile et le jeu vidéo. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Volant d'une voiture équipé d'un coussin gonflable de sécurité, airbag, et d'un avertisseur sonore mais sans bouton Volant d'un véhicule équipé d'un dispositif de coussin gonflable, d'un avertisseur sonore et de boutons de commandes/consignes audio et vitesse Dans une automobile, le vol...

The Leopard (Il Gattopardo)Poster film pertamaSutradaraLuchino ViscontiProduserGoffredo LombardoPietro NotarianniDitulis olehPasquale Festa CampanileEnrico MedioliMassimo FranciosaLuchino ViscontiSuso Cecchi d'AmicoBerdasarkanThe Leopardby Giuseppe Tomasi di LampedusaPemeranBurt LancasterClaudia CardinaleAlain DelonSerge ReggianiMario GirottiPierre ClementiPenata musikNino RotaSinematograferGiuseppe RotunnoPenyuntingMario SerandreiDistributorTitanus (Italia - bioskop)Medusa Entertainmen...

King of Assyria, 1074/3–1056 BCE Ashur-bel-kalaKing of AssyriaKing of the Four Corners of the WorldKing of the Middle Assyrian EmpireReign1074–1056 BCPredecessorAsharid-apal-EkurSuccessorEriba-Adad IISpouseBabylonian princess, daughter of Adad-apla-iddina[1]FatherTiglath-Pileser IAššūr-bēl-kala, inscribed maš-šur-EN-ka-la and meaning “Aššur is lord of all,”[2] was the king of Assyria 1074/3–1056 BC, the 89th to appear on the Assyrian Kinglist. He was the son ...

Torrance CoombsCoombs, 2012Lahir14 Juni 1983 (umur 40)Vancouver, British Columbia, KanadaPekerjaanAktorTahun aktif1994 - sekarangSitus webhttp://www.torrancecoombs.com torrancecoombs.com Torrance Coombs (lahir 14 Juni 1983) adalah aktor televisi, teater, dan film asal Kanada. Filmografi Film The Familiar (2009) sebagai Sam Matheson; film pendek Good Image Media (2009) sebagai Pj; film pendek Serial televisi Supernatural (2007; one episode) sebagai Mitch Battlestar Galactica (2008; ...

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Waidhofen an der Ybbs Waidhofen an der Ybbs adalah sebuah kota di Austria Hilir, Austria. Kota ini memiliki luas sebesar 131.52 km². Kota ini memiliki populasi sebesar 11.662 jiwa. Pranala luar www.waidhofen.at lbsKota dan distrik (Bezirke) di Austria HilirKrems an der Donau · St. Pölten · ...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

Part of a series onRail transport History Company types Infrastructure Management Rail yard Railway station list Railway track Maintenance Track gauge Variable gauge Gauge conversion Dual gauge Service and rolling stock Operating Locomotives Steam locomotives Trains Railroad cars Railway couplings Couplers by country Coupler conversion Dual coupling Wheelset Bogie (truck) Passenger train Commuter rail Regional rail Inter-city rail High-speed railways Passenger traffic terminology Named passe...

5th Roman emperor from AD 54 to 68 For other uses, see Nero (disambiguation). NeroHead of Nero from an oversized statue. Glyptothek, MunichRoman emperorReign13 October 54 – 9 June 68PredecessorClaudiusSuccessorGalbaBorn15 December AD 37Antium, Italy, Roman EmpireDied9 June AD 68 (aged 30)outside Rome, ItalyBurialMausoleum of the Domitii Ahenobarbi, Pincian Hill, RomeSpousesClaudia OctaviaPoppaea SabinaStatilia MessalinaSporusPythagorasIssueClaudia AugustaNamesLucius Domitius Aheno...

الدوري العراقي الممتاز السلسلة دوري نجوم العراق الموسم 1997–98 البلد العراق الفرق 16 الفائز الشرطة(اللقب الثاني) هابطون الموصلالكوتالصناعة بطولة الأندية الآسيوية الشرطة كأس أبطال الكؤوس الآسيوية الزوراء هداف الدوري محمود مجيد(22 هدف) 1996–97 1998–99 تعديل مصدري - تعديل...

Ski area in Vermont, United States Bolton ValleyThe Main Lodge at Bolton Valley ResortLocationBolton, Vermont, U.S.Nearest major cityBurlington, Vermont, U.S. (21 miles)Coordinates44°25′11″N 72°51′00″W / 44.419621°N 72.849998°W / 44.419621; -72.849998Vertical1,625 feet (495 m)[1]Top elevation3,150 feet (960 m)[2]Base elevation1,446 feet (441 m)[2]Skiable area165 acres (0.67 km2)Trails71[3]Lift system6...

Confederate Navy sailors Salvador Pirates was the name given to the band of Confederate Navy sailors that attempted to seize a Panama Railroad coastal steamer on the high seas. Their intent was then to arm her and attack the Pacific Mail steamers and the American whalers in the North Pacific. In spring of 1864, the Confederate Navy ordered Captain Thomas Egenton Hogg and his command to take passage on board a coastal steamer in Panama City, seize her on the high seas, arm her and attack the P...

Cet article est une ébauche concernant l’art et une chronologie ou une date. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Chronologies Données clés 1853 1854 1855 1856 1857 1858 1859Décennies :1820 1830 1840 1850 1860 1870 1880Siècles :XVIIe XVIIIe XIXe XXe XXIeMillénaires :-Ier Ier IIe IIIe Chronologies géographiques Afrique Afrique du S...

Questa voce o sezione sull'argomento centri abitati del Trentino-Alto Adige non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Sfruzcomune Sfruz – Veduta LocalizzazioneStato Italia Regione Trentino-Alto Adige Provincia Trento AmministrazioneSindacoAndrea Biasi (lista civica) dal 7-11-2016 TerritorioCoordinate46°20′N 11°07′E4...

アラバマ物語 To Kill a Mockingbird ポスター(1963)監督 ロバート・マリガン脚本 ホートン・フート原作 ハーパー・リー製作 アラン・J・パクラ出演者 グレゴリー・ペックメアリー・バダムフィリップ・アルフォード音楽 エルマー・バーンスタイン撮影 ラッセル・ハーラン編集 アーロン・ステル配給 ユニバーサル映画公開 1962年12月25日 1963年6月22日上映時間 129分製作国 アメ�...
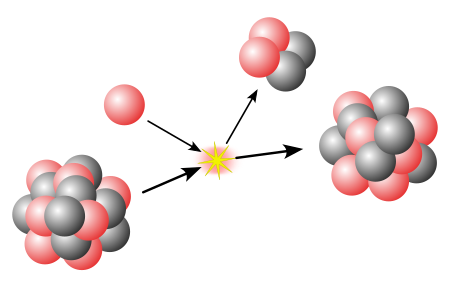
Nuclear physics Nucleus Nucleons p n Nuclear matter Nuclear force Nuclear structure Nuclear reaction Models of the nucleus Liquid drop Nuclear shell model Interacting boson model Ab initio Nuclides' classification Isotopes – equal Z Isobars – equal A Isotones – equal N Isodiaphers – equal N − Z Isomers – equal all the above Mirror nuclei – Z ↔ N Stable Magic Even/odd Halo Borromean Nuclear stability Binding energy p–n ratio Drip line Island of stability Valley...