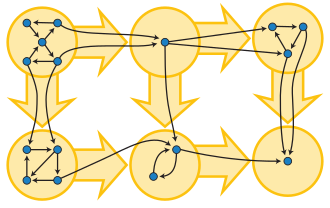
Strongly connected component
|
Read other articles:

Untuk serial Comedy Central, lihat This Is Not Happening (serial TV). This is Not HappeningEpisode The X-FilesNomor episodeMusim 8Episode 14SutradaraKim MannersPenulisChris CarterFrank SpotnitzKode produksi8ABX14Tanggal siar25 Februari 2001Durasi44 menitKronologi episode ← SebelumnyaPer Manum Selanjutnya →Deadalive This Is Not Happening adalah episode keempat belas dari musim kedelapan dan episode ke-175 secara keseluruhan dari serial televisi fiksi ilmiah The X-Files. Epis...

Riho Abiru Riho Abiru (阿比留李帆; lahir 17 Juli 1993) adalah seorang penyanyi dan idol Jepang. Ia adalah mantan anggota grup J-pop SKE48.[1] Ia sekarang berafiliasi dengan Starray Production. Riwayat Tim SKE48 Kenkyuusei → Tim KII → Tim S → Tim KII → Kelulusan Masuk SKE48 sebagai Kenkyuusei pada Maret 2009 (Generasi ke-2) Dipromosikan ke Tim KII pada 6 Desember 2010 Ditransfer ke Tim S pada 13 April 2013 (Perombakan Tim SKE48) Ditransfer ke Tim KII pada 24 Februari 2014 ...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Papua New Guinea–United Kingdom relations – news · newspapers · books · scholar · JSTOR (December 2015) (Learn how and when to remove this template message) Bilateral relationsPapua New Guinea – United Kingdom relations Papua New Guinea United Kingdom Papua New Guinea high ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2017. Osmar Aparecido de AzevedoInformasi pribadiTanggal lahir 23 Juli 1980 (umur 43)Tempat lahir BrasilPosisi bermain PenyerangKarier senior*Tahun Tim Tampil (Gol)2006 Oita Trinita * Penampilan dan gol di klub senior hanya dihitung dari liga domestik Osm...

Japanese carrier-based dive bomber D4Y Suisei Yokosuka D4Y3 Model 33 Suisei Role Dive bomber, reconnaissance, night fighterType of aircraft National origin Japan Manufacturer Yokosuka First flight December 1940 Introduction 1942 Retired 1945 Status Retired Primary user Imperial Japanese Navy Air Service Produced 1942–1945 Number built 2,038 The Yokosuka D4Y Suisei (彗星, Suisei, Comet, Allied reporting name Judy) is a two-seat carrier-based dive bomber developed by the Yokosuka Naval...

أندرس دبليو. بيرثيلسن معلومات شخصية الميلاد 28 سبتمبر 1969 (55 سنة)[1][2] مواطنة مملكة الدنمارك الحياة العملية المهنة ممثل، وممثل أفلام، ومؤدي أصوات، ومخرج أفلام اللغات الدنماركية الجوائز جائزة روبرت لأفضل ممثل في دور رئيسي (عن عمل:A Lucky Man) (2023) ا...

Association football league in England This article uses citations that link to broken or outdated sources. Please improve the article by addressing link rot or discuss this issue on the talk page. (August 2021) (Learn how and when to remove this message) Football leagueBrighton, Worthing & District Football LeagueFounded2014Country EnglandDivisions1Number of teams16Level on pyramidLevel 14Feeder toWest Sussex Football League Championship SouthDomestic cup(s)Brighton College CupPresi...

HartwellStasiun komuter PTVLokasiGeorgina Parade, CamberwellMelbourne, VictoriaAustraliaKoordinat37°50′39″S 145°04′32″E / 37.8441°S 145.0756°E / -37.8441; 145.0756Koordinat: 37°50′39″S 145°04′32″E / 37.8441°S 145.0756°E / -37.8441; 145.0756PemilikVicTrackOperatorMetro TrainsJalur AlameinJumlah peron2Jumlah jalur2KonstruksiJenis strukturTanahInformasi lainZona tarifMyki Zona 1Situs webPublic Transport VictoriaSe...
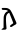
Alphabet used for writing the Gothic language For other uses, see Gothic script. GothicScript type Alphabet Time periodFrom c. 350, in decline by 600DirectionLeft-to-right LanguagesGothicRelated scriptsParent systemsGreek script augmented with Latin and possibly Runic (questionable)GothicISO 15924ISO 15924Goth (206), GothicUnicodeUnicode aliasGothicUnicode rangeU+10330–U+1034F This article contains phonetic transcriptions in the International Phonetic Alphabet (IPA).&...

Athletics at the1970 Summer UniversiadeTrack events100 mmenwomen200 mmenwomen400 mmenwomen800 mmenwomen1500 mmen5000 mmen10,000 mmen100 m hurdleswomen110 m hurdlesmen400 m hurdlesmen3000 msteeplechasemen4×100 m relaymenwomen4×400 m relaymenField eventsHigh jumpmenwomenPole vaultmenLong jumpmenwomenTriple jumpmenShot putmenwomenDiscus throwmenwomenHammer throwmenJavelin throwmenwomenCombined eventsPentathlonwomenDecathlonmenvte The men's javelin throw event at the 1970 Summer Universiade wa...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يناير 2020) التنافس بين تونس ومصر في كرة القدمالفرق المتنافسة الجزائر ليبياأول لقاءالجزائر 2–1 ليبيا، مباراة ود...

Audience NetworkDiluncurkan25 November 1999 (1999-11-25)PemilikDirecTVFormat gambar720p HDTV(downscaled to letterboxed 480i for the SDTV feed)NegaraAmerika SerikatBahasaInggrisKantor pusatEl Segundo, CaliforniaNama sebelumnyaFreeview (1999–2005)The 101 Network (2005–11)Audience Network (2011–16) Audience Network (lebih dikenal sebagai Audience dari 2016 hingga 2020)[1] adalah saluran televisi berbayar Amerika yang dimiliki oleh AT&T. Ini menampilkan campuran serial asli...
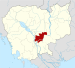
City in Kampong Cham, CambodiaSkuon ស្គន់CityNickname: SpidervilleSkuonLocation within CambodiaCoordinates: 12°3′4″N 105°4′15″E / 12.05111°N 105.07083°E / 12.05111; 105.07083Country CambodiaProvinceKampong ChamDistrictCheung Prey Fried spiders for sale at the market in SkuonSkuon (Khmer: ស្គន់) is the district capital of Cheung Prey District, in Kampong Cham Province, Cambodia. This busy market town has grown up around the inte...

In this Chinese name, the family name is Zhou. Zhou Xiaoxuan周晓璇Zhou in 2022Born1992 or 1993 (age 30–31)WuhanOccupation(s)screenwriter, activistKnown forRole in Chinese Me Too movementZhou Xiaoxuan (Chinese: 周晓璇; pinyin: Zhōu Xiǎoxuán; born c. 1993), better known by her pen name Xianzi (Chinese: 弦子; pinyin: Xiánzi), is a Chinese screenwriter and leading advocate in the Chinese Me Too movement.[1][2][3] Bi...

Women's 800 metres at the European Athletics Championships 1969 EuropeanAthletics ChampionshipsTrack events100 mmenwomen200 mmenwomen400 mmenwomen800 mmenwomen1500 mmenwomen5000 mmen10,000 mmen100 m hurdleswomen110 m hurdlesmen400 m hurdlesmen3000 msteeplechasemen4 × 100 m relaymenwomen4 × 400 m relaymenwomenRoad eventsMarathonmen20 km walkmen50 km walkmenField eventsHigh jumpmenwomenPole vaultmenLong jumpmenwomenTriple jumpmenShot putmenwomenDiscus throwmenwomenHammer throwmenJavelin...

Artikel utama: Pemilihan umum Presiden Indonesia 2019 Pemilihan umum Presiden Indonesia di Maluku 20192014202417 April 2019 (2019-04-17)Jajak pendapatTerdaftar1.266.034[1]Suara terhitung100%per 26/05/19, 07:00 WIBKandidat Calon Joko Widodo Prabowo Subianto Partai PDI-P Gerindra Aliansi Koalisi Indonesia Kerja[2] Koalisi Indonesia Adil Makmur[2] Pendamping Ma'ruf Amin Sandiaga Uno Suara popular 599.457 392.940 Persentase 60,40% 39,60% Presiden...

Una taza de té con mantequilla tibetano El té de mantequilla (denominado también de forma local Po cha - བོད་ཇ་ - o Sutschia, a veces también como su you cha 酥油茶; pinyin: sū yóu chá) o goor goor en términos locales de Ladakh es un té tradicional del Tíbet y de las minorías chinas del sudoeste de China, que se elabora con mantequilla de leche de yak y al que se le añade un poco de sal. El té con mantequilla es parte indispensable de la vida de los tibetanos, ya q...

2024年 3月(弥生) 日 月 火 水 木 金 土 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 日付の一覧 各月 1 2 3 4 5 6 7 8 9 10 11 12 3月30日(さんがつさんじゅうにち)は、グレゴリオ暦で年始から89日目(閏年では90日目)にあたり、年末まであと276日ある。 できごと 正十七角形が定規とコンパスだけで作図可能と発見(1796) パリ条約(1856)が締結されクリミア戦�...

У этого термина существуют и другие значения, см. Юань-ди. Лю Ши 11-й император эпохи Хань Дата рождения 75 до н. э.(-075) Место рождения Чанъань, Китайская империя[вд] Дата смерти 33 до н. э.(-033) Место смерти Чанъань, Китайская империя[вд] Время царствования 48-33 гг. до н.э. Предшестве�...

この項目では、2009年まで百貨店「そごう」を運営していた企業について説明しています。 2009年以降そごう・西武が運営する「そごう」ブランドの店舗については「そごうの店舗一覧」をご覧ください。 その他の用法については「十合」をご覧ください。 フォートレス・インベストメント・グループ > そごう・西武 > そごう この項目には、一部のコンピュ...