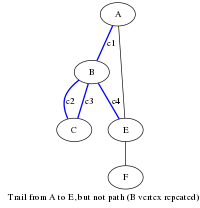
Path (graph theory)
|
Read other articles:

Australian racecar driver Geoff BrabhamBrabham at the 2014 Indianapolis 500Nationality AustralianBorn (1952-03-20) 20 March 1952 (age 71)Sydney, AustraliaRetired2001Related toJack Brabham (father)Matthew Brabham (son)Gary Brabham (brother)David Brabham (brother)Sam Brabham (nephew) Lisa Thackwell (sister in law)Australian Super Touring ChampionshipYears active1995–1997TeamsBMW Motorsport AustraliaStarts48Wins9Best finish2nd in 1995 & 1997 Australian Super Touring ChampionshipPrevio...

The German involvement in Abkhazia dates back to the 1870s, when Russian Tsar Alexander II decided to settle German villagers in Abkhazia to civilize the newly conquered Caucasian peoples. The German Empire was briefly involved in a military intervention in 1918. More recently, Germany has been involved in diplomatic and peacekeeping efforts to resolve the dispute between the so-called Republic of Abkhazia and Georgia, Germany's strategic ally.[1] Early Involvement Kress von Kressenst...

Pemuda HitlerHitlerjugendLogo Pemuda HitlerDibentuk4 Juli 1926Negara Jerman NaziTipe unitOrganisasi pemuda, paramiliterJumlah personel8 juta (1940)Divisi HitlerjugendDivisi Hitlerjugend SS Panzer ke-12MotoBlut und Ehre(Darah dan Kehormatan)MarkasKaufhaus Jonaß, BerlinCabang Pemuda Jerman Liga Putri Jerman Dibubarkan10 Oktober 1945TokohReichsjugendführer Baldur von Schirach (pertama) Artur Axmann (terakhir)Stabsführer Karl Nabersberg (pertama) Kurt Petter (terakhir)InsigniaBenderaLamba...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (يونيو 2019) عائض القحطاني معلومات شخصية الجنسية سعودي الديانة الإسلام منصب • بروفيسور واستشاري جراحات المناظير وجراحات علاج السمنة في كلية الطب، جامعة الملك سعود، الحي

Telephone numbers in Germany8 geographic zonesLocationCountryGermanyContinentEuropeRegulatorFederal Network AgencyTypeOpenNSN length3 to 13[1]Format(xx…) xx…Access codesCountry code49International access00Long-distance0List of Germany dialing codes The regulation of telephone numbers in Germany is the responsibility of the Federal Network Agency (German: Bundesnetzagentur, BNetzA) of the German government. The agency has a mandate to telecommunications in Germany and other infrast...

Protein-coding gene in the species Homo sapiens HSP90B1Available structuresPDBOrtholog search: PDBe RCSB List of PDB id codes4NH9IdentifiersAliasesHSP90B1, ECGP, GP96, GRP94, HEL-S-125m, HEL35, TRA1, heat shock protein 90kDa beta family member 1, heat shock protein 90 beta family member 1External IDsOMIM: 191175 MGI: 98817 HomoloGene: 2476 GeneCards: HSP90B1 Gene location (Human)Chr.Chromosome 12 (human)[1]Band12q23.3Start103,930,107 bp[1]End103,953,931 bp[1]Gene locat...

You can help expand this article with text translated from the corresponding article in Japanese. Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Consider adding a topic to this template: there are already 3,676 arti...

Socialist political party in Sweden Left Party VänsterpartietAbbreviationVLeaderNooshi DadgostarFoundersZeth HöglundCarl WinbergFounded1917; 106 years ago (1917)Split fromSwedish Social Democratic PartyHeadquartersKungsgatan 84, StockholmYouth wingYoung LeftMembership (2021) 28,873[1]IdeologySocialism[2]Eco-socialism[3]Feminism[4]Euroscepticism[5]Political positionLeft-wing[6]European affiliationMaintenant le Peuple...

Proposed country Comintern project on Balkan Federation The establishment of a Balkan Federation has been a recurrent topic among the peoples of the Balkans. The concept of a Balkan federation emerged in the late 19th century among left political forces in the region. The central aim was to establish a new political unity: a common federal republic unifying the Balkan Peninsula on the basis of internationalism, socialism, social solidarity, and economic equality. The underlying vision was tha...

2010 Russian action film The Alien GirlFilm posterRussianЧужая Directed byAnton BormatovWritten byVladimir NesterenkoSergei SokolyukProduced byKonstantin ErnstAlexey KucherenkoIgor TolstunovStarringNatalia RomanychevaEvgeniy TkachukKirill PolukhinAnatoliy OtradnovCinematographyAnastasi MikhalovDistributed by20th Century FoxRelease date 17 June 2010 (2010-06-17) Running time100 minsCountryRussiaLanguageRussian The Alien Girl (Russian: Чужая, romanized: Chuzhaya) i...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: レオポルト・フォン・ブーフ – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2011年10月) クリスティアン・レオポル�...

Verlauf und Einzugsgebiet der Elbe Elbquelle: Wappen der Elbstädte am Wasserloch Die folgende Liste von Städten und Orten an der Elbe soll mal alle Regionen, Städte und Orte an der Elbe von der Quelle in Tschechien bis zur Mündung in die Nordsee auflisten, aktuell macht sie das aber noch nicht. Inhaltsverzeichnis 1 Wichtige Regionen und Großstädte 1.1 Regionen 1.2 Großstädte 2 Städte und Orte 2.1 Tschechien 2.2 Deutschland Wichtige Regionen und Großstädte Regionen Metropolregion Ha...

Questa voce sugli argomenti comunismo e Unione Sovietica è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Il Politburo del Comitato centrale del PCUS (in russo Политическое бюро (Политбюро) ЦК КПСС?, Političeskoe bjuro (Politbjuro) CК KPSS, lett. Ufficio politico del CC del PCUS) era l'organismo dirigente del Partito Comunista dell'Unione Sovietica nei periodi fra le riun...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (December 2012) (Learn how and when to remove this template message) 1st Marine Infantry Parachute Regiment1er Régiment de Parachutistes d'Infanterie de MarineRegimental beret badgeActiveSeptember 15, 1940 – presentCountry FranceBranch French ArmyTypeSpecial ForcesSize865 authorized personnel (2017)Part&#...

1990 Indian filmThangathin ThangamDirected bySirajScreenplay bySirajStory byRadha BharathiProduced byK. PrabhakaranStarringRamarajanRagasudhaCinematographyB. S. LokanathEdited byL. KesavanMusic byS. A. RajkumarProductioncompanyAnbalaya FilmsRelease date 14 April 1990 (1990-04-14) CountryIndiaLanguageTamil Thangathin Thangam is a 1990 Indian Tamil-language action drama film directed by Siraj, starring Ramarajan and Ragasudha. It was released on 14 April 1990.[1] Plot Thi...

Johan Bure, 1568–1652.You can help expand this article with text translated from the corresponding article in Swedish. (May 2022) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Consider adding a topic to this...

Anna Friel Friel en 2015Información personalNombre de nacimiento Anna Louise FrielNacimiento 12 de julio de 1976 (47 años)Rochdale (Inglaterra)Nacionalidad BritánicaFamiliaPareja David Thewlis (2001-2010)Rhys Ifans (2011-2014)Hijos 1EducaciónEducada en Holy Cross College, UK Información profesionalOcupación Actriz, actriz de teatro y actriz de cine Años activa desde 1986Sitio web www.annafriel.orgPremios artísticosPremios Emmy Mejor Actuación de una Actriz2017 MarcellaDistincion...

Defunct United States railroad Southern RailwayA Southern Railway train in 1969OverviewHeadquartersWashington, D.C., U.S.Key people J.P. MorganPrimary financier (1894-1913) Fairfax HarrisonPresident (1913-1937) FoundersCharles H. CosterSamuel SpencerFrancis Lynde StetsonReporting markSOULocaleWashington, D.C., Virginia, North Carolina, South Carolina, Georgia, Florida, Alabama, Mississippi, Tennessee, Kentucky, Ohio, Illinois, Indiana, Missouri and LouisianaDates of operation1894–1982Su...

政府統計處Census and Statistics Department 香港特別行政區政府機構政府統計處標誌處長余振強副處長周錦添助理處長余司帆 吳品慧 劉國信 蕭惠芬 陳麗珊部門資訊成立日期1967年12月所屬部門財經事務及庫務局總部 香港香港島灣仔港灣道12號灣仔政府大樓16至22及25樓聯絡資訊網站www.censtatd.gov.hk/home/index_tc.jsp 政府統計處(簡稱統計處;英語:Census and Statistics Department,C&S...

Dua patung makam keramik dari Dinasti Han Timur (25–220 M) digambarkan sednag memainkan liubo Liubo (Hanzi: 六博 atau 陸博; Pinyin: liù bó; Wade–Giles: liu po; harfiah: 'enam batang') adalah sebuah permainan papan Tiongkok kuno yang dimainkan oleh dua pemain. Permainan tersebut ditemukan tak lebih dari pertengahan milenium ke-1 SM, dan populer pada zaman dinasti Han (202 SM – 220 M). Pranala luar Wikimedia Commons memiliki media mengenai Liubo. Liubo Illustrated ar...