Square-free polynomial
|
Read other articles:

Gubernur TennesseeLambang negara bagianBendera GubernurPetahanaBill Leesejak 19 Januar 2019GelarGubernur(informal)The Honorable(formal)StatusKepala Negara BagianKepala PemerintahanKediamanMansion Gubernur TennesseeMasa jabatan4 tahun, bisa menjabat lagi sekaliDasar hukumKonstitusi Tennessee 1796Pejabat perdanaJohn SevierDibentuk30 Maret 1796; 227 tahun lalu (1796-03-30)WakilWakil Gubernur TennesseeGaji$178,356 (2013)[1] Berikut merupakan daftar gubernur negara bagian Tenness...

Artikel ini bukan mengenai Kucing kashmir. Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Kucing kasymir – berita · surat kabar · buku · cendekiawan · JSTOR Kasymir Nama lain Bulu panjang bengal Asal Amerika Serikat Kucing domestik (Felis catus) Kuc...

Bupati Bengkulu UtaraLambang Kabupaten Bengkulu UtaraPetahanaIr. H. Miansejak 17 Februari 2016KediamanBalai Daerah Bengkulu Utara Kota ArgamakmurMasa jabatan5 tahunDibentuk1949Pejabat pertamaT. UsmanSitus webbengkuluutarakab.go.id Berikut ini adalah daftar Bupati Bengkulu Utara dari masa ke masa. No Bupati Mulai Jabatan Akhir Jabatan Prd. Ket. Wakil Bupati 1 T.Usman 1960 1965 1 – 2 Kol.Kamarsyah 1965 1967 2 3 Kol.Syamsul Bahrun 1967 1972 3 4 Mayor.Boerhan Dahri 197...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of spouses of prime ministers of Croatia – news · newspapers · books · scholar · JSTOR (May 2021) (Learn how and when to remove this template message) The current spouse of the Prime Minister of Croatia is Ana Maslać. Spouses of presidents (*) as spouse of the President o...

Sua Altezza SerenissimaWenzel Anton von Kaunitz-Rietberg Ministro di Stato e degli Esteri della Monarchia AsburgicaDurata mandato13 maggio 1753 –19 agosto 1793 Capo di StatoMaria Teresa (1753–1780)Giuseppe II (1780–1790)Leopoldo II (1790-1792)Francesco II (1792-1793) ViceJohann Philipp von Cobenzl (1779-1793) PredecessoreAnton Corfitz Ulfeldt SuccessoreJohann Philipp von Cobenzl Ambasciatore austriaco in FranciaDurata mandato1750 –1752 Capo di StatoMaria Te...
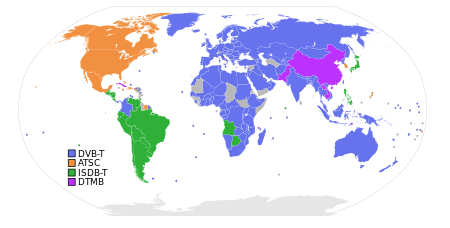
For the list of analog television stations, see List of analog television stations in the Philippines. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: List of digital television stations in the Philippines – news · new...

President of Cape Verde from 2001 to 2011 For the Canadian film director, see Pedro Pires (director). Pedro PiresPires in 20053rd President of Cape VerdeIn office22 March 2001 – 9 September 2011Prime MinisterJosé Maria NevesPreceded byAntónio Mascarenhas MonteiroSucceeded byJorge Carlos FonsecaPrime Minister of Cape VerdeIn office8 July 1975 – 4 April 1991PresidentAristides PereiraAntónio Mascarenhas MonteiroPreceded byOffice establishedSucceeded byCarlos Veiga Person...

إلين جونسون سيرليف (بالإنجليزية: Ellen Johnson-Sirleaf) مناصب رئيس ليبيريا (24 ) في المنصب16 يناير 2006 – 22 يناير 2018 غيد براينت جورج ويا معلومات شخصية الميلاد 29 أكتوبر 1938 (86 سنة)[1][2][3][4] مونروفيا الإقامة واشنطن العاصمةنيروبيمونروفيا �...

National governing body of cycle racing in Uruguay This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Uruguayan Cycling Federation – news · newspapers · books · scholar · JSTOR (June 2011) (Learn how and when to remove this message) The Uruguayan Cycling Federation (in Spanish: Federación Ciclista Uruguaya) is the national gove...

Vowel sound represented by ⟨ɜ⟩ in IPA Open-mid central unrounded vowelɜIPA Number326Audio sample source · helpEncodingEntity (decimal)ɜUnicode (hex)U+025CX-SAMPA3Braille Image IPA: Vowels Front Central Back Close i y ɨ ʉ ɯ u Near-close ɪ ʏ ʊ Close-mid e ø ɘ ɵ ɤ o Mid e̞ ø̞ ə ɤ̞ o̞ Open-mid ɛ œ ɜ ɞ ʌ ɔ Near-open æ ɐ Open a ɶ ä ɑ ɒ IPA help audio full chart template Legend: unrounded • rounded The open-mid central u...

Village and civil parish in Lancashire, England This article is about the village near Clitheroe. For the town formerly in Lancashire and known as Barrow, see Barrow-in-Furness. Human settlement in EnglandBarrowBay Horse public house, BarrowBarrowShown within Ribble ValleyShow map of the Borough of Ribble ValleyBarrowLocation within LancashireShow map of LancashireOS grid referenceSD736384Civil parishBarrowDistrictRibble ValleyShire countyLancashireRegionNorth WestCountryEnglan...

لمعانٍ أخرى، طالع الحرب الأهلية العراقية (توضيح). الحرب الأهلية العراقية جزء من حرب الخليج الثالثة و صراعات الجماعات المسلحة العراقية تحت سيطرة الشيعة تحت سيطرة السنة تحت سيطرة الأكراد تحت سيطرة السريان تحت سيطرة اليزيديين تح...

Radio station in San Francisco For the airport in Manistique, Michigan, assigned ICAO code KISQ, see Schoolcraft County Airport. KISQSan Francisco, CaliforniaBroadcast areaSan Francisco Bay AreaFrequency98.1 MHz (HD Radio)Branding98.1 The BreezeProgrammingFormatSoft adult contemporaryAffiliationsPremiere NetworksOwnershipOwneriHeartMedia, Inc.(iHM Licenses, LLC)Sister stationsKIOI, KKSF, KMEL, KNEW, KOSF, KYLDHistoryFirst air dateJuly 17, 1958 (1958-07-17) (as KAFE)Former call ...

В Википедии есть статьи о других людях с фамилией Райан. Фрэнсис Райан Общая информация Полное имя Фрэнсис Джон Райан Прозвище Hun[1] Родился 10 января 1908(1908-01-10)Филадельфия, Пенсильвания, США Умер 14 октября 1977(1977-10-14) (69 лет)Филадельфия, Пенсильвания, США Гражданство США Р�...

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (October 2019) (Learn how and when to remove this message) The Dynamo Shooting Range is a firing range located in Mytishchi in the then Eastern Planning Zone of Moscow, Russia. Constructed in 1957 and renovated in 1979, it hosted the shooting and the shooting part of the modern ...

Jurustandur No. 18Album studio karya SlankDirilis1 Juli 2010Direkam2009-2010GenrePop, RockLabelSlank RecordsUniversal Music IndonesiaNagaswaraKronologi Slank Anthem For The Broken Hearted (2008)Anthem For The Broken Hearted2008 Jurustandur No. 18 (2010) I Slank U (2012)I Slank U2012 Jurustandur No. 18 adalah album musik utamanya karya Slank kedelapan belas. Dirilis tahun 2010 yang berisikan 17 buah lagu. Lagu utamanya di album ini ialah JURUSTANDUR. Sebelum dirilis dalam Bentuk album, 7 l...

此條目没有列出任何参考或来源。 (2013年8月27日)維基百科所有的內容都應該可供查證。请协助補充可靠来源以改善这篇条目。无法查证的內容可能會因為異議提出而被移除。 克鲁扎利亚Cruzália市镇克鲁扎利亚在巴西的位置坐标:22°44′08″S 50°47′37″W / 22.735555555556°S 50.793611111111°W / -22.735555555556; -50.793611111111国家巴西州圣保罗州面积 • 总计149.173&#...

Trần Huy NgạnChức vụGiám đốc Công an Tỉnh Hưng YênNhiệm kỳ – 15 tháng 12 năm 2014Vị tríHưng Yên Thông tin chungSinh1954 (69–70 tuổi)Đảng chính trị Đảng Cộng sản Việt NamBinh nghiệpPhục vụCông an nhân dân Việt NamCấp bậcThiếu tướng Trần Huy Ngạn (sinh 1954) là một Thiếu tướng Công an nhân dân Việt Nam, nguyên Ủy viên Ban Thường vụ Tỉnh uỷ, nguyên Giám đốc Công an T�...

Pour les articles homonymes, voir Ricardo et Montalban. Ricardo Montalbán Ricardo Montalbán dans L'Île fantastique en 1977. Données clés Nom de naissance Ricardo Gonzalo Pedro Montalbán Merino Surnom Valentin Naissance 25 novembre 1920Mexico, Mexique Nationalité Mexicaine Américaine Décès 14 janvier 2009 (à 88 ans)Los Angeles, (Californie), États-Unis Profession ActeurRéalisateur Films notables La Planète des singesStar Trek II : La Colère de KhanY a-t-il un flic pou...

此条目页的主題是2012年首播电视剧《穆桂英挂帅》。关于穆桂英挂帅的其他含义,請見「穆桂英挂帅」。 穆桂英掛帥类型武侠,古装,喜剧编剧张建广导演宫晓东主演苗圃、羅晉、張鐵林制作国家/地区 中国语言普通话集数39集每集长度40分钟片头曲《大姊大》苗圃片尾曲《你的名字》雷佳、阎维文制作拍摄/制作年份2011年拍攝地點金牌拍攝地制作公司兄弟时�...





























