Polynomial long division
|
Read other articles:

Logo Kereta Listrik Keihan Keihan seri 8000 Keihan seri 2600 Keihan seri 800 Stasiun Yawatashi Bus Keihan PT Kereta Api Listrik Keihan. (京阪電気鉄道株式会社code: ja is deprecated , Keihan Denki Tetsudō Kabushiki-gaisha) adalah sebuah operator kereta api asal Jepang yang beroperasi di Prefektur Osaka, Kyoto, dan Shiga. Umumnya dikenal sebagai Keihan (京阪code: ja is deprecated ), Keihan Dentetsu (京阪電鉄code: ja is deprecated ) atau Keihan Densha (京阪電車code: ja is dep...

Lambang kebesaran La Brosse-Montceaux. La Brosse-MontceauxNegaraPrancisArondisemenProvinsKantonMontereau-Fault-YonneAntarkomuneCommunauté de communes des Deux FleuvesPemerintahan • Wali kota (2008-2014) Bernard Metay • Populasi1599Kode INSEE/pos77054 / 2 Population sans doubles comptes: penghitungan tunggal penduduk di komune lain (e.g. mahasiswa dan personil militer). La Brosse-Montceaux merupakan sebuah komune di departemen Seine-et-Marne di region Île-de-Fran...

Untuk kegunaan lain, lihat Airlink. Airwaves Airlink IATA ICAO Kode panggil - WLA AIRLIMITED PenghubungLusakaArmada1Tujuan1SloganZambia Airwaves Airlink adalah maskapai penerbangan yang berbasis di Zambia. Layanan Airwaves Airlink mengoperasikan layanan dari Lusaka ke Ndola (per Maret 2005). Armada Armada Airwaves Airlink terdiri dari satu pesawat yaitu Beechcraft 1900C-1. Maskapai ini sedang berusaha untuk mencari pesawat baru dengan kisaran 30 kursi.[1] Referensi ^ Airliner World, M...

Sporting event delegationGhana at the2017 World Aquatics ChampionshipsFlag of GhanaFINA codeGHANational federationGhana Swimming Federationin Budapest, HungaryCompetitors4 in 1 sportMedals Gold 0 Silver 0 Bronze 0 Total 0 World Aquatics Championships appearances197319751978198219861991199419982001200320052007200920112013201520172019202220232024 Ghana competed at the 2017 World Aquatics Championships in Budapest, Hungary from 14 July to 30 July. Swimming Main article: Swimming at the 2017 Wor...

Questa voce o sezione sugli argomenti storia economica e economia internazionale non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Il sistema aureo è un sistema monetario nel quale la base monetaria è data da una quantità fissata d'oro. Indice 1 Descrizione 1.1 Vantaggi 1.2 Svantaggi 2 Storia 2.1 Il sistema gold standard 2.2 Le principali monete nel gol...

Bombardier CRJ 1000 NexGen milik Garuda Indonesia Bombardier CRJ Bombardier CRJ (Canadair Regional Jet) merupakan sebuah pesawat regional yang diproduksi oleh Bombardier, dan berdasarkan oleh Canadian Challenger business jet. Pesawat ini terbang pertama kali pada tanggal 10 Mei 1991. Ada dua jenis Bombardier CRJ di pasaran, yaitu CRJ100/CRJ200 dan CRJ700/CRJ900/CRJ1000. Operator Amerika Utara ALMA de Mexico Air Canada Jazz American Eagle Air Wisconsin Comair Compass Airlines (Northwest Airlin...

Helen DahmHelen Dahm en Inde, 1938BiographieNaissance 21 mai 1878Egelshofen (d)Décès 24 mai 1968 (à 90 ans)MännedorfSépulture Oetwil am SeeNationalité suisseActivité PeintrePériode d'activité 1898-1968Autres informationsMouvement ExpressionnismeVue de la sépulture.modifier - modifier le code - modifier Wikidata Pour les articles homonymes, voir Dahm. Helen Dahm (ou Helene Dahm ; 21 mai 1878 à Egelshofen - 24 mai 1968 à Männedorf) est une peintre suisse expressionniste. ...

Overview of land sea and air transport systems in Virginia The current Virginia passenger vehicle license plate, introduced in 2002. Transportation in the Commonwealth of Virginia is by land, sea and air. Virginia's extensive network of highways and railroads were developed and built over a period almost 400 years, beginning almost immediately after the founding of Jamestown in 1607, and often incorporating old established trails of the Native Americans. History Colonial period, 19th century ...

Cuba vehicle license plates New Cuban licence plates that use FE-Schrift (since 2013) miniatur miniatur miniatur miniatur miniatur The current vehicle registration plate system of Cuba was introduced in May 2013. Current plates are European standard 520 mm × 110 mm, completely replacing the previous system introduced in 2002.[1] The international vehicle registration code for Cuba is C. New registration system The new system uses a standard manufacturer format, where the al...

London Underground station This article is about the London Underground station. For the former station in West Yorkshire, see Queensbury railway station. Queensbury QueensburyLocation of Queensbury in Greater LondonLocationQueensburyLocal authorityBrentManaged byLondon UndergroundNumber of platforms2Fare zone4London Underground annual entry and exit2018 4.20 million[1]2019 4.11 million[2]2020 2.86 million[3]2021 1.84 million[4]2022 3.07 million[5]Railw...

Instrumen Abdikasi Undang-Undang Deklarasi Abdikasi Yang Mulia (bahasa Inggris: His Majesty's Declaration of Abdication Act 1936) (1 Edw. 8 & 1 Geo. 6 c. 3) adalah Undang-Undang Parlemen Britania Raya yang mengesahkan dan meratifikasi abdikasi Raja Edward VIII dan mengesahkan suksesi kepada saudaranya Pangeran Albert, Adipati York (yang kemudian menjadi Raja George VI). UU tersebut juga mengecualikan para keturunan mendatang dari Edward dari garis suksesi. Edward VIII melakukan abdika...

Zone of Oromia Region, Ethiopia Map of the regions and zones of Ethiopia. West Guji is located in the Oromia Region. West Guji is one of the zones of the Oromia Region of Ethiopia. Located in southern Oromia, West Guji is bordered on the south by Borena, on the west by the South Ethiopia Regional State, on the north by the Gedeo Zone of South Ethiopia and Sidama Region and on the east by the Guji Zone. Its administrative center is Bule Hora.[1] The West Guji Zone was created by nine d...

Hervé Renard Nazionalità Francia Altezza 180 cm Calcio Ruolo Allenatore (ex difensore) Squadra Francia femminile Termine carriera 1998 - giocatore CarrieraSquadre di club1 1985-1988 Cannes 2? (?)1988-1990 Cannes87 (0)1991-1997 Stade de Vallauris105 (2)1997-1998 Draguignan? (?)Carriera da allenatore 2002-2003 Shanghai LianchengVice2004 Cambridge UtdVice2004-2007 Cambridge Utd2007-2010 Zambia2010-2011 Angola2011-2013 Zambia2013-2014 Sochaux2014-2015 C...

14th-century Persian historian Copy of Wassaf's Tarikh-i Wassaf, created in 17th-century Safavid Iran Wassaf or Vassaf (Persian: عبدالله ابن فضلالله شرفالدین شیرازی) Abdallah ibn Faḍlallah Sharaf al-Din Shīrāzī (fl. 1265–1328) was a 14th-century Persian historian of the Ilkhanate. Waṣṣāf, sometimes lengthened to Waṣṣāf al-Ḥaḍrat or Vassaf-e Hazrat (Persian: وصّافِ حضرت), is a title meaning Court Panegyrist.[1][2&#...

「俄亥俄」重定向至此。关于其他用法,请见「俄亥俄 (消歧义)」。 俄亥俄州 美國联邦州State of Ohio 州旗州徽綽號:七葉果之州地图中高亮部分为俄亥俄州坐标:38°27'N-41°58'N, 80°32'W-84°49'W国家 美國加入聯邦1803年3月1日,在1953年8月7日追溯頒定(第17个加入联邦)首府哥倫布(及最大城市)政府 • 州长(英语:List of Governors of {{{Name}}}]]) •&...

German footballer Emmanuel Iyoha Iyoha with Fortuna Düsseldorf in 2016Personal informationFull name Emmanuel Edosa Iyoha[1]Date of birth (1997-10-11) 11 October 1997 (age 26)Place of birth Düsseldorf, GermanyHeight 1.91 m (6 ft 3 in)Position(s) ForwardTeam informationCurrent team Fortuna DüsseldorfNumber 19Youth career2012–2015 Fortuna DüsseldorfSenior career*Years Team Apps (Gls)2015–2018 Fortuna Düsseldorf II 16 (4)2015– Fortuna Düsseldorf 83 (6)2017�...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Senate election 2010 United States Senate election in Washington ← 2004 November 2, 2010 2016 → Nominee Patty Murray Dino Rossi Party Democratic Republican Popular vote 1,314,930 1,196,164 Percentage 52.08% 47.37% County resultsMurray: 50–60% 60–70% Rossi: 40–50% 50–60% 60–70% &...

LighthouseKullen Lighthouse Kullen LighthouseLocationKullaberg KattegattSwedenCoordinates56°18′04.0″N 12°27′05.4″E / 56.301111°N 12.451500°E / 56.301111; 12.451500TowerConstructed1563 (first)1585 (second)1749 (third)1792 (fourth)1843 (fifth)Constructiongranite and brick towerAutomated1979Height18.5 metres (61 ft)Shapecylindrical tower with balcony and lantern attached to a 2-storey buildingMarkingsgrey unpainted stone tower, white lantern, black l...
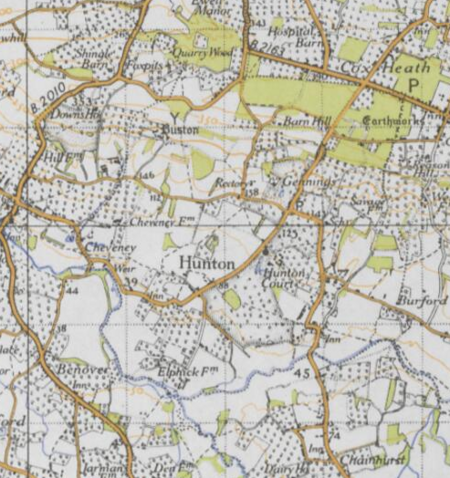
Village and civil parish in Kent, England Human settlement in EnglandHuntonCottages on West StreetHuntonLocation within KentPopulation702 (2011)[1]Civil parishHuntonShire countyKentRegionSouth EastCountryEnglandSovereign stateUnited KingdomPost townMaidstonePostcode districtME15PoliceKentFireKentAmbulanceSouth East Coast UK ParliamentMaidstone and The Weald List of places UK England Kent 51°13′00″N 0°28′00″E / 51.216667°N 0.466667°E...



















