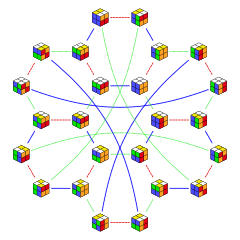
Nauru graph
| |||||||||||||||||||||||||||||
Read other articles:

Coca de albaricoque Coca d'albercocs, coca d'alberche coca de albaricoque de Son CarrióTipo pan dulceConsumoOrigen EspañaGastronomía aragonesa, mallorquina, leridanaDatos generalesIngredientes harina de trigo albaricoque sebo patata azúcar[editar datos en Wikidata] La coca de albaricoque es una coca o torta dulce típica de la isla de Mallorca, el área de Lérida y algunas zonas de Aragón, en España (en aragonés, coca d'alberche; en catalán coca d'albercocs). Se elabo...

Cabo Rozewie Przyladek Rozewie Vista del cabo desde la playa ChłapowoUbicación administrativaPaís Polonia PoloniaDivisión PomeraniaUbicación geográficaContinente Europa orientalMar / océano Mar BálticoCoordenadas 54°50′00″N 18°20′00″E / 54.833333333333, 18.333333333333Mapa de localización Cabo Rozewie Geolocalización en Polonia[editar datos en Wikidata] El cabo Rozewie (en polaco: Przyladek Rozewie[1]) es un promontorio del nores...

Manduel Manduel (Frankreich) Staat Frankreich Region Okzitanien Département (Nr.) Gard (30) Arrondissement Nîmes Kanton Marguerittes Gemeindeverband Nîmes Métropole Koordinaten 43° 49′ N, 4° 28′ O43.8194444444444.4741666666667Koordinaten: 43° 49′ N, 4° 28′ O Höhe 50–77 m Fläche 26,46 km² Einwohner 7.092 (1. Januar 2020) Bevölkerungsdichte 268 Einw./km² Postleitzahl 30129 INSEE-Code 30155 Website www.manduel.fr Ratha...

Serbian actor Boris IsakovićБорис ИсаковићIsaković in 2007Born (1966-12-14) 14 December 1966 (age 56)Novi Sad, SR Serbia, SFR YugoslaviaOther namesBoroOccupationActorYears active1990-presentSpouseJasna Đuričić (m. 1996) Boris Isaković (Serbian: Борис Исаковић; born 14 December 1966) is a Serbian actor.[1] He has appeared in more than thirty films since 1990. Personal life He is married to Serbian actress Jasna Đuričić and together they...

Частина серії статей на тему:Кримські татариКримські татари, 1862 Символіка Герб Гімн Прапор Етнічні групи Добруджацькі татари Липки Ногаї Тати Ялибойлу Діаспора: Болгарія США Узбекистан Туреччина Близькі етноси: Балкарці Караїми Ногайці Історія Початок етногенезу Захі...

British tour operator based in Wallington, Surrey Newmarket Holidays, part of The Newmarket Group, is a British tour operator based in Wallington, Greater London, providing escorted holidays, resort-based stays and event-based tours to destinations throughout the UK, in Europe and to worldwide destinations. The group employs 180 staff at its Surrey head office. History Foundation, Ownership and Industry Accreditations Toni Frei and Jeremy Griffin founded Newmarket Promotions Limited, the pare...

2018 United States Supreme Court caseMinnesota Voters Alliance v. ManskySupreme Court of the United StatesArgued February 28, 2018Decided June 14, 2018Full case nameMinnesota Voters Alliance, et al., Petitioners v. Joe Mansky, et al.Docket no.16-1435Citations585 U.S. ___ (more)138 S. Ct. 1876; 201 L. Ed. 2d 201; 86 U.S.L.W. 4401Case historyPriorMinnesota Majority v. Mansky, 849 F.3d 749 (8th Cir. 2017); cert. granted, 138 S. Ct. 446 (2017).HoldingMinnesota's ban on political apparel at pollin...

School in the United StatesNew Hope-Solebury High SchoolLocation182 W Bridge St New Hope, Pennsylvania, PA 18938United StatesInformationSchool districtNew Hope-Solebury School DistrictPrincipalPatrick SasseFaculty39.70 (FTE)[1]Grades9-12Number of students499 (2020–21)[1]Student to teacher ratio12.57[1]Color(s)Blue and Gold MascotLionsAffiliationPublicWebsitehttp://nhsd.org/ New Hope-Solebury High School is a public high school located at 182 West Bridge S...

JuhuJuhuTampilkan peta MumbaiJuhuTampilkan peta MaharashtraJuhuTampilkan peta IndiaKoordinat: 19°06′N 72°50′E / 19.10°N 72.83°E / 19.10; 72.83Koordinat: 19°06′N 72°50′E / 19.10°N 72.83°E / 19.10; 72.83NegaraIndiaNegara bagianMaharashtraDistrikMumbai SuburbanMetroMumbaiBahasa • ResmiMarathiZona waktuUTC+5:30 (IST)Juhu adalah sebuah daerah kelas atas yang terletak di Mumbai. Daerah ini paling terkenal dengan Pantai Juhu...

Medieval school of philosophy Scholastics redirects here. For other uses, see Scholastic. Not to be confused with Scholarism. 14th-century image of a university lecture Part of a series onScholasticism Schools Thomism Scotism Occamism Major works Summa Theologica Cur Deus Homo Summa Grammatica Summa logicae Opus Oxoniense Libri Quattuor Sententiarum Precursors Augustine of Hippo Boethius Pope Gregory I Alcuin of York John Scotus Eriugena Philosophers Thomas Aquinas (Doctor Angelicus) Duns Sco...

Dewi RemajaFormation1985; 38 years ago (1985)TypeBeauty pageantHeadquartersKuala Lumpur, MalaysiaLocationMalaysiaOfficial language MalayOwnerNu Ideaktiv Sdn. Bhd.AffiliationsRemaja (magazine)WebsiteOfficial website Dewi Remaja is a beauty pageant and reality television show in which a number of aspiring Malaysian women compete for the title of Dewi Remaja and the opportunity to start a career in the modelling or acting industry based in Malaysia. Created and organized by the...

A.W.27 Ensign Role AirlinerType of aircraft Manufacturer Armstrong Whitworth Aircraft First flight 24 January 1938 Introduction 1938 Retired 1946 Primary users Imperial AirwaysBritish Overseas Airways Corporation (BOAC) Produced 1938-1940 Number built 14 The Armstrong Whitworth A.W.27 Ensign was a British four-engine monoplane airliner and the largest airliner built in Britain during the Interwar period.[1] The British airline Imperial Airways requested tenders for a large monopl...

Japanese pop singer AKINOBackground informationBirth nameAkino Kawamitsu (川満 愛希信, Kawamitsu Akino)Also known asAKINOBorn (1989-12-31) December 31, 1989 (age 33)Utah, United States[1]OriginOkinawa Prefecture, JapanGenresPopOccupation(s)SingerYears active2005-presentLabelsVictor (2005)flying dog (2007)Websitehttp://bless4.jp/Musical artist Akino Kawamitsu (川満 愛希信, Kawamitsu Akino), known mononymously as Akino (stylized in all uppercase), is a Japanese singer. Hi...

Cinta Rasul 5Album studio karya Haddad Alwi & SulisDirilis2003 2007 (rilis ulang)Direkam2003GenreNasyid ReligiLabelMusika Selaras Citra Warner Music Indonesia (rilis ulang)ProduserHaydar YahyaKronologi Haddad Alwi & Sulis Cinta Rasul(2002)Cinta Rasul2002 Cinta Rasul 5 Cinta Rasul 6 (2004)Cinta Rasul 62004 Cinta Rasul 5 adalah sebuah album religi karya Haddad Alwi & Sulis yang dirilis pada tahun 2003. Album ini menggandeng arranger musik yakni Idrus Alhabsyi & Dwiki Dharmaw...

Liberian men's under-18 basketball team LiberiaFIBA zoneFIBA AfricaWorld ChampionshipsAppearancesNoneAfrican ChampionshipsAppearancesNone The Liberia men's national under-18 basketball team is a national basketball team of Liberia, administered by the Liberia Basketball Federation.[1] It represents the country in international under-18 (under age 18) basketball competitions. It appeared at the 2012 FIBA Africa Under-18 Championship qualification stage. See also Liberia men's national ...

2009 single by GacktFlowerSingle by Gacktfrom the album Re:Born ReleasedJuly 1, 2009GenreHard rock, Progressive rockLabelDearsSongwriter(s)Gackt C.Producer(s)GacktGackt singles chronology Lost Angels (2009) Flower (2009) The Next Decade (2009) Music videoFlower on YouTube Flower is the thirty-fourth single by Japanese recording artist Gackt, released on July 1, 2009.[1] This single is the final of the four singles of the countdown to Gackt's 10th anniversary as solo artist.[2]...

Species of fish Stareye lightfish Scientific classification Kingdom: Animalia Phylum: Chordata Class: Actinopterygii Order: Stomiiformes Family: Phosichthyidae Genus: PollichthysGrey, 1959 Species: P. mauli Binomial name Pollichthys mauli(Poll, 1953) Synonyms Yarrella mauli The stareye lightfish (Pollichthys mauli) is a species in the monotypic genus of Pollichthys. They are small stomiiform fishes found in oceans throughout the world. The maximum length is 6 cm.[1] Etymolog...

AN/MPQ-64 Sentinel adalah sebuah radar tiga dimensi yang digunakan untuk mengingatkan dan antrian senjata Short Range Air Defense (SHORAD) ke lokasi target bermusuhan mendekati kekuatan lini depan mereka. Radar Sentinel ini digunakan dengan luas maju unit pertahanan udara dari Angkatan Darat AS dan USMC. Radar menggunakan berbagai-gated, sistem pulsa-doppler X-band. Antena menggunakan frekuensi fase teknologi pemindaian elektronik, membentuk balok pensil 3D tajam meliputi pengawasan yang besa...

Mahasweta DeviMahasweta DeviLahir(1926-01-14)14 Januari 1926Dhaka, Kepresidenan Bengal, India Britania (sekarang Bangladesh)Meninggal28 Juli 2016(2016-07-28) (umur 90)Kolkata, IndiaPekerjaanAktivis politik, pengarang, diplomatPeriode1956–2016Genrenovel, cerita pendek, drama, esayTemaSuku-suku terdenotifikasi di IndiaAliran sastraGananatyaKarya terkenalHajar Churashir Maa(Mother of 1084)Aranyer Adhikar(Hak Hutan)Titu MirPasanganBijon BhattacharyaAnakNabarun BhattacharyaTanda&#...

1995 studio album by SexepilSugar for the SoulStudio album by SexepilReleased12 February 1995 (Hungary)Recorded1994GenreIndie rockLength47:16LabelWarner Bros. RecordsProducerBrian AndersonSexepil chronology Against Nature(1993) Sugar for the Soul(1995) Your Scream Is Music(2014) Singles from Sugar for the Soul JerusalemReleased: 1 December 1994 Professional ratingsReview scoresSourceRatingMetal Hammer(6/7)[1] Sugar for the Soul is the fifth studio album recorded by Sexepil. Th...