Equinumerosity
|
Read other articles:

7DAYS EuroCup1Season2020–21Dates29 September 2020 – 30 April 2021Number of games182Number of teams24Regular seasonSeason MVP Jamar SmithFinalsChampions AS Monaco (1st title) Runners-up UNICSSemifinalists Herbalife Gran Canaria Virtus Segafredo BolognaFinals MVP Rob GrayAwardsRising Star Aleksander BalcerowskiRecordsBiggest home winBahçeşehir 108–74 Reyer Venezia(15 December 2020)Biggest away winPromitheas 69–105 Cedevita Olimpija(16 December 2020)Highest scoringGiants An...

Mexican singer, actress and recording artist In this Spanish name, the first or paternal surname is Rivera and the second or maternal family name is Munguía. DannaBackground informationBirth nameDanna Paola Rivera MunguíaBorn (1995-06-23) 23 June 1995 (age 28)Mexico City, MexicoGenres Latin pop Pop Teen pop Occupations Actress singer model Instruments Vocals piano guitar Years active1999–presentLabelsUniversal Music MexicoPartner(s)Alex HoyerMusical artist Danna Paola Rivera ...
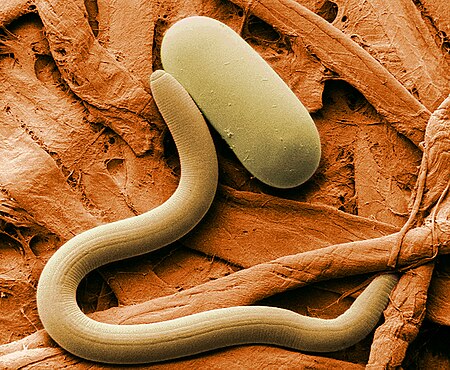
Nematoda TaksonomiSuperkerajaanEukaryotaKerajaanAnimaliaSuperfilumEcdysozoaFilumNematoda Rudolphi, 1808 Tata namaSinonim takson Nematodes Burmeister, 1837 Nemates Cobb, 1919 Nemata Cobb, 1919 Kelas Chromadorea Dorylaimea Enoplea atau Adenophorea Secernentea (lihat teks)lbs Nematoda merupakan kelompok cacing yang berada dalam filum Nematoda (terkadang juga disebut Nemathelminthes).[1] Filum ini memiliki anggota beragam yang menghuni rentang lingkungan yang sangat luas. Menurut taksonom...

1978 film by Édouard Molinaro La Cage aux FollesFrench theatrical release posterDirected byÉdouard MolinaroScreenplay by Marcello Danon Édouard Molinaro Jean Poiret Francis Veber Based onLa Cage aux Folles1973 playby Jean PoiretProduced byMarcello DanonStarring Ugo Tognazzi Michel Serrault Claire Maurier Rémi Laurent Carmen Scarpitta Michel Galabru CinematographyArmando NannuzziEdited by Monique Isnardon Robert Isnardon Music byEnnio Morricone[1]Productioncompanies Les Productions...

Government ministry of the Republic of Turkey Ministry of Culture and TourismKültür ve Turizm BakanlığıRepublic of Turkey Ministry of Culture and Tourism building, AnkaraAgency overviewFormed2003JurisdictionGovernment of TurkeyHeadquartersAnkaraAnnual budget38.964.106.000 TL (2024)Minister responsibleMehmet Nuri ErsoyDeputy Ministers responsibleBatuhan MumcuGökhan YazgıNadir AlpaslanSerdar ÇamWebsitektb.gov.tr The Ministry of Culture and Tourism (Turkish: Kültür ve Turizm Bakanlığ...

Poem by J.R.R Tolkien For the state of roving in search of chivalrous adventure, see knight-errant. Errantry is a three-page poem by J.R.R. Tolkien, first published in The Oxford Magazine in 1933.[T 1] It was included in revised and extended form in Tolkien's 1962 collection of short poems, The Adventures of Tom Bombadil. Donald Swann set the poem to music in his 1967 song cycle, The Road Goes Ever On. The poem has a complex metre, invented by Tolkien. It fits the tune of Gilbert and ...

Conflicts in Libya from 2011 onwards Libyan Civil War redirects here. For other uses, see Libyan Civil War (disambiguation).Libyan Revolt redirects here. For the revolt of troops in Libya against Carthage, see Mercenary War.Military situation in Libya as of June 2020. Under the control of the Tobruk-led Government and Libyan National Army Under the control of the Government of National Accord and Allies Under the control of the National Salvation Government/...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Association football club in England Football clubWantage Town FCFull nameWantage Town Football ClubNickname(s)The FredsFounded1892GroundAlfredian Park, Wantage 51°34′55.7″N 1°25′48.8″W / 51.582139°N 1.430222°W / 51.582139; -1.430222Capacity1,500ManagerDaniel BarryLeagueHellenic League Premier Division2022–23Hellenic League Premier Division, 10th of 20WebsiteClub website Home colours Away colours Wantage Town Football Club is a football club based in Want...

Questa voce o sezione sull'argomento militari italiani non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Luigi Giulio di SavoiaSoprannomele Chevalier de Savoie[1] NascitaTolosa, 2 maggio 1660 MorteVienna, 13 luglio 1683 Cause della morteCaduta da cavallo durante un inseguimento Luogo di sepo...

Rule of thumb in driving The three second rule is a time for the defensive driver to judge the minimum safe trailing distance to help avoid collisions under ideal driving conditions. The red car's driver picks a tree to judge a two-second safety buffer. The two-second rule is a rule of thumb by which a driver may maintain a safe trailing distance at any speed.[1][2] The rule is that a driver should ideally stay at least two seconds behind any vehicle that is directly in front ...

「俄亥俄」重定向至此。关于其他用法,请见「俄亥俄 (消歧义)」。 俄亥俄州 美國联邦州State of Ohio 州旗州徽綽號:七葉果之州地图中高亮部分为俄亥俄州坐标:38°27'N-41°58'N, 80°32'W-84°49'W国家 美國加入聯邦1803年3月1日,在1953年8月7日追溯頒定(第17个加入联邦)首府哥倫布(及最大城市)政府 • 州长(英语:List of Governors of {{{Name}}}]]) •&...

Charity Shield FA 1974TurnamenCharity Shield FA Liverpool Leeds United 1 1 Liverpool menang 6–5 pada adu penaltiTanggal10 Agustus 1974StadionStadion Wembley, London← 1973 1975 → Charity Shield FA 1974 adalah pertandingan sepak bola antara Liverpool dan Leeds United yang diselenggarakan pada 10 Agustus 1974 di Stadion Wembley, London. Pertandingan ini merupakan pertandingan ke-52 dari penyelenggaraan Charity Shield FA. Pertandingan ini dimenangkan oleh Liverpool dengan skor 6–5...

Russian actor (born 1941) This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Sergei Nikonenko – news · newspapers · books · scholar · JSTOR (August 2022) (Learn how and when to remove this message)...

1974 one-day rock music festival This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: California Jam – news · newspapers · books · scholar · JSTOR (April 2011) (Learn how and when to remove this message) California JamCalifornia Jam 1974GenreHard rock, progressive rock, heavy metalDatesApril 6, 1974Location(s)Ont...

Neighbourhood in Istanbul, Turkey Neighbourhood in Üsküdar, Istanbul, TurkeyAltunizadeNeighbourhoodAltunizadeLocation in TurkeyShow map of TurkeyAltunizadeAltunizade (Istanbul)Show map of IstanbulCoordinates: 41°01′13″N 29°02′44″E / 41.02028°N 29.04556°E / 41.02028; 29.04556CountryTurkeyProvinceIstanbulDistrictÜsküdarPopulation (2022)13,459Time zoneUTC+3 (TRT)Postal code34662Area code0216 Altunizade is a neighbourhood in the municipality and distri...

You can help expand this article with text translated from the corresponding article in Chinese. (January 2021) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Do not translate text that appears unreliable or lo...

Protein-coding gene in the species Homo sapiens SUCLG1IdentifiersAliasesSUCLG1, GALPHA, MTDPS9, SUCLA1, succinate-CoA ligase alpha subunit, succinate-CoA ligase GDP/ADP-forming subunit alphaExternal IDsOMIM: 611224; MGI: 1927234; HomoloGene: 55785; GeneCards: SUCLG1; OMA:SUCLG1 - orthologsGene location (Human)Chr.Chromosome 2 (human)[1]Band2p11.2Start84,423,528 bp[1]End84,460,045 bp[1]Gene location (Mouse)Chr.Chromosome 6 (mouse)[2]Band6|6 C1Start73,225,36...
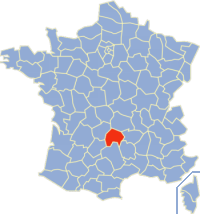
Untuk keju, silakan lihat Cantal (keju) Cantal (15) (dalam bahasa Occitan Cantal / Cantau / Chantal / Chantau) ialah sebuah département di Prancis, terletak di région Auvergne, dan mendapatkan namanya dari pegunungan Cantal. Letak Cantal di Prancis Sejarah Artikel utama: Sejarah Cantal Département ini diciptakan setelah Revolusi Prancis, pada 4 Maret 1790 dan diterapkan hukum pada 22 Desember 1789, dibentuk dari provinsi Auvergne, bekas provinsi yang kemudian bernama Haute-Auvergne. Politi...

Javier OtxoaJavier Otxoa en 2009InformationsNom de naissance Javier Otxoa PalaciosNaissance 30 août 1974BarakaldoDécès 24 août 2018 (à 43 ans)Alhaurin de la TorreNationalité espagnoleÉquipes professionnelles 1997-2001Kelme-Costa BlancaPrincipales victoires 1 étape du Tour de France Champion paralympique de contre-la-montre CP3 2004 et 2008modifier - modifier le code - modifier Wikidata Javier Otxoa Palacios, né le 30 août 1974 à Barakaldo et mort le 24 août 2018 à Alhaurín ...










