Reflexive relation
|
Read other articles:

Untuk other orang dengan nama yang sama, lihat Margaret Sullivan (disambiguasi). Margaret SullavanSullavan pada tahun 1940LahirMargaret Brooke Sullavan(1909-05-16)16 Mei 1909Norfolk, Virginia, ASMeninggal1 Januari 1960(1960-01-01) (umur 50)New Haven, Connecticut, ASSebab meninggalOverdosis barbituratMakamSaint Mary's Whitechapel Episcopal ChurchyardKebangsaanAmerika SerikatPendidikanChatham Episcopal InstitutePekerjaanAktrisTahun aktif1929–1960Suami/istriHenry Fonda &#...
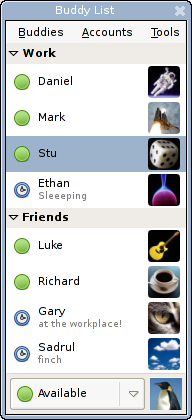
Common feature of email, and IM; a collection of contacts or screen names This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Contact list – news · newspapers · books · scholar · JSTOR (July 2008) (Learn how and when to remove this template message) A contact list in Pidgin 2.0 A contact list is a collection of screen names. It i...

Заккарія Гізольфі Народження: 15 століття Смерть: невідомо Мати: Bikhakhanimd Таманський півострів, карта 1870 року Заккарія Гізольфі (Zaccaria de Guizolfi, Zaccaria de Ghisolfi, Захарія Гуйгурсіс, Захарія Гуїл Гурсіс, у документах московського посольського наказу Князь Таманський Захарія) —

ЗарбеленZarbeling Країна Франція Регіон Гранд-Ест Департамент Мозель Округ Саррбур-Шато-Сален Кантон Дьєз Код INSEE 57759 Поштові індекси 57340 Координати 48°53′30″ пн. ш. 6°41′18″ сх. д.H G O Висота 235 - 325 м.н.р.м. Площа 3,87 км² Населення 66 (01-2020[1]) Густота 17,31 ос./км...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مارس 2018) ماريا كوفاتسو (باليونانية Μαρία Κουβάτσου) (باليونانية: Μαρία Κουβάτσου) ماريا كوفاتسو في أولمبياد الشطرنج عام 2016 في باكو معلومات شخصية الميلاد 2 نوفمبر 1...

روفانو الإحداثيات 39°59′00″N 18°15′00″E / 39.983333333333°N 18.25°E / 39.983333333333; 18.25 [1] تقسيم إداري البلد إيطاليا[2] التقسيم الأعلى مقاطعة لتشه خصائص جغرافية المساحة 39.73 كيلومتر مربع (9 أكتوبر 2011)[3] ارتفاع 127 متر عدد السكان عدد السكان 9...

AwardLiège MedalLiège Medal(obverse)TypeUnofficial campaign medalAwarded for1914 defence of the city of LiègeCountry BelgiumEligibilityBelgian military personnelCampaign(s)World War IStatusNo longer awardedEstablishedApril 1920First awardedApril 1920Liège Medal(reverse) Lieutenant General Gérard Leman, heroic commander of the defence of Liège The Liège Medal (French: Médaille de Liège, Dutch: Medaille van Luik) was an unofficial World War I campaign medal issued by the Belgian c...

アバロンの初期配置 アバロン(Abalone)は、「玉による相撲」ともいえる内容の2人用のボードゲームである。二人零和有限確定完全情報ゲームに分類されるアブストラクトゲームである。 ルールは単純であり、通常2,3分で覚えることができる。また、チェスや将棋のような他のゲームに比べ展開が早く、1ゲームにかかる時間も少ない。 内容 ルール アバロンは、61の穴(

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Artikel ini tidak memiliki bagian pembuka yang sesuai dengan standar Wikipedia. Mohon tulis paragraf pembuka yang informatif sehingga pembaca dapa...

إسقاط طائرة ميل-مي 17 العسكرية اليمنية صورة أرشيف لطائرة ميل مي-17 ملخص الحادث التاريخ 6 أغسطس 2013 نوع الحادث أطلاق نار الموقع صافر، محافظة مأرب الوفيات 11 (جميع الركاب والطاقم) النوع ميل مي-17 تعديل مصدري - تعديل وقعت حادثة إسقاط طائرة ميل-مي 17 العسكرية اليمنية عندما تعرضت لإ�...

Indian yogi and author (born 1957) This article is about Sadhguru, an Indian spiritual teacher. For the definition of the word, see Satguru. SadhguruBornJagadish Vasudev (1957-09-03) 3 September 1957 (age 66)Mysore, Mysore State, IndiaAlma materUniversity of Mysore (BA)OrganizationIsha FoundationNotable workInner EngineeringDhyanalingaRally for RiversLinga BhairaviAdiyogi: The Source of YogaMystic's MusingsCauvery CallingSpouse Vijaya Kumari (m. 1984;...

SafaruddinAnggota Dewan Perwakilan RakyatPetahanaMulai menjabat 1 Oktober 2019Daerah pemilihanKalimantan TimurKepala Kepolisian Daerah Kalimantan TimurMasa jabatan3 September 2015 – 5 Januari 2018PendahuluAndayonoPenggantiPriyo WidyantoWakil Kepala Badan Intelijen dan Keamanan PolriMasa jabatan22 Januari 2015 – 3 September 2015PendahuluDjoko Mukti HaryonoPenggantiDjoko PrastowoWakil Kepala Kepolisian Daerah Kalimantan BaratMasa jabatan8 Juni 2010 – 15 Febr...

American children's television show OobiGenre Puppetry Comedy Created byJosh SeligDeveloped byEssie Chambers[1]Written by Jenna Bradley Natascha Crandall Olga Humphrey Christine Nee Sascha Paladino Melinda Richards Directed by Pam Arciero Tim Lagasse Kevin Lombard Scott Preston Josh Selig Starring Tim Lagasse Stephanie D'Abruzzo Noel MacNeal Tyler Bunch ComposersSacred Noise, Inc.Country of originUnited StatesOriginal languageEnglishNo. of seasons3[a]No. of episodesShorts: 48L...

Sports Illustrated KidsThe first issue of Sports Illustrated for Kids, January 1, 1989, showing NBA Superstar Michael Jordan with friends Brad Pielet and Nancy Deller.Managing EditorBob DerStaff writersStaff Managing Editor SI.com: Paul Fichtenbaum Managing Editor: Bob DerCreative Director: Beth Power BuglerSenior Producer: Paul UlaneExecutive Marketing Director: Eileen MasioCategoriesSports magazineFrequencybi-monthlyCirculation950,000First issueJanuary 1, 1989 (1989-January-0...

В Википедии есть статьи о других людях с такой фамилией, см. Перелыгин. Евгений Юрьевич Перелыгинукр. Євген Юрійович Перелигін Чрезвычайный и Полномочный Посол Украины в Республике Сан-Марино 6 декабря 2013 — 15 июля 2020 Предшественник Георгий Чернявский Преемник Ярослав...

British writer and academic For other uses, see Simon Gray (disambiguation). Simon GrayCBE FRSLBornSimon James Holliday Gray(1936-10-21)21 October 1936Hayling Island, Hampshire, EnglandDied7 August 2008(2008-08-07) (aged 71)London, EnglandOccupationPlaywright, screenwriter, memoirist, novelistacademic (1965–1985)NationalityEnglishEducationWestminster SchoolAlma materDalhousie University (B.A., 1957) Trinity College, Cambridge (B.A., 1961)Period1963–2008GenreDrama, screenplay, me...

UAE-based satellite telecommunications company This article is about the satellite communications system. For the constellation, see Pleiades and Pleiades in folklore and literature. Thuraya Telecommunications CompanyTypeSubsidiaryIndustryMobile-satellite servicesFounded1997; 26 years ago (1997)HeadquartersUnited Arab EmiratesWebsitewww.thuraya.com Thuraya (Arabic: الثريا, Gulf Arabic pron.: [ɐθ.θʊˈrɑj.jɐ]; from the Arabic name for the constellation of t...

Residential skyscraper in Manhattan, New York The Orion(2008)General informationStatusCompletedTypeResidential[1]Location350 West 42nd StreetNew York City, New York, U.S.Coordinates40°45′30″N 73°59′33″W / 40.758361°N 73.992603°W / 40.758361; -73.992603Construction started2004[1]Opening2006[1]HeightAntenna spire604 ft (184 m)[1]Technical detailsFloor count58[1]Floor area632,939 sq ft (58,802.0 ...

Batalyon Kavaleri 5/Dwipangga CetaLambang Yonkav 5/Dwipangga CetaDibentuk9 Februari 1950CabangKavaleriTipe unitSatuan Bantuan TempurPeranPasukan Lapis BajaBagian dariKodam II/SriwijayaMarkasMuara Enim, Sumatera SelatanJulukanYonkav 5/DPCMotoJaya dimasa Perang Berguna dimasa DamaiBaretHitamMaskotGajah SumateraUlang tahun9 FebruariAlutsistaTank AMX-13 75mm, Tank AMX-13 105mm, Tank AMX-13 APC dan Panser Anoa Batalyon Kavaleri 5/Dwipangga Ceta atau Yon Kav 5/Serbu merupakan satuan bantuan tempur ...

















































