Combinatorial class
|
Read other articles:

Disambiguazione – Se stai cercando altri significati, vedi San Diego (disambigua). Questa voce o sezione sull'argomento centri abitati della California non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. San Diegocomune(EN) City of San Diego (dettagli) San Diego – Veduta LocalizzazioneStato Stati Uni...

Josef DobrovskýPotret Josef Dobrovský oleh František TkadlíkLahir(1753-08-17)17 Agustus 1753Balassagyarmat, Kerajaan HungariaMeninggal6 Januari 1829(1829-01-06) (umur 75)Brno, Kekaisaran AustriaMinat utamafilologi, sejarah Dipengaruhi Johann Christoph Adelung[1] Josef Dobrovský Josef Dobrovský (17 Agustus 1753 – 6 Januari 1829) adalah seorang filolog dan sejarawan Ceko yang menjadi tokoh penting dalam Kebangkitan Nasional Ceko bersama Josef Jungmann. K...

Neighbourhood of George Town in Penang, MalaysiaTaman Tun SardonNeighbourhood of George TownOther transcription(s) • Mandarin敦沙顿花园 (Simplified)敦沙頓花園 (Traditional)Dūn shā dùn huā yuán (Pinyin)Astaka Taman Tun Sardon, a wet market-cum-hawker centre.Taman Tun SardonLocation within George Town in PenangCoordinates: 5°22′8.4828″N 100°18′21.1962″E / 5.369023000°N 100.305887833°E / 5.369023000; 10...
Battle of GalațiPart of the Romanian Campaign of World War Iand the Russian Civil WarMonument commemorating the Battle of Galați, photo from 1921Date12–22 January 1918LocationGalați, Kingdom of RomaniaResult Romanian victory: Russian troops disarmedBelligerents Romania Russian RepublicCommanders and leaders Constantin Prezan Constantin Niculescu-Rizea Dmitry Shcherbachev Yevgeni Iskritsky Strength 500 troops 12,000 troopsCasualties and losses Unknown Unknown, but R...

Untuk berbagai daftar negara menurut ciri-ciri tertentu, lihat Daftar negara. Berikut ini merupakan daftar yang menampilkan ikhtisar mengenai negara-negara berdaulat di seluruh dunia, beserta informasi mengenai status dan pengakuan atas kedaulatan negara-negara tersebut. Daftar tersebut memuat sejumlah 206 negara berdaulat yang dapat dikelompokkan berdasarkan keanggotaannya dalam Sistem Perserikatan Bangsa-Bangsa, yaitu: 193 negara anggota PBB,[1] dua negara pengamat nonanggota Majeli...

Puteri Indonesia BantenLogo Puteri IndonesiaSingkatanPI BantenDinamai berdasarkanPuteri Indonesia RegionalTanggal pendirian2001; 23 tahun lalu (2001)Didirikan diKota Serang, Banten, IndonesiaTipeKontes Kecantikan RegionalKantor pusatKota Serang, IndonesiaLokasi IndonesiaJumlah anggota Puteri IndonesiaBahasa resmi Bahasa IndonesiaBahasa InggrisPresiden dan CEO Puteri IndonesiaMooryati SoedibyoKetua Puteri IndonesiaPutri KuswisnuwardhaniOrganisasi indukPuteri IndonesiaSitus webwww.put...
List of events ← 1828 1827 1826 1825 1824 1829 in Ireland → 1830 1831 1832 1833 1834 Centuries: 17th 18th 19th 20th 21st Decades: 1800s 1810s 1820s 1830s 1840s See also:1829 in the United KingdomOther events of 1829 List of years in Ireland Events from the year 1829 in Ireland. Events 13 April – the Roman Catholic Relief Act, granting Catholic Emancipation, becomes law, thanks to Daniel O'Connell and the Catholic Association.[1] Roman Catholics are eligible to sit in the...

Un déchet radioactif est un déchet qui, du fait du niveau de sa radioactivité, nécessite des mesures de radioprotection[1] particulières. Ces déchets doivent réglementairement faire l'objet d'une caractérisation radiologique (par le producteur de déchets) et d'un contrôle (par le centre de stockage), afin d'assurer que leur stockage est adapté à leur radioactivité éventuelle, et ne crée pas de risque radiologique. Le cas échéant, dans de nombreux pays, des « déchets nu...

American lawyer and politician (1843–1926) Robert Lincoln redirects here. For other uses, see Robert Lincoln (disambiguation). Robert Todd LincolnRobert Lincoln c. 1870–188030th United States Minister to the United Kingdom In officeMay 25, 1889 – May 4, 1893PresidentBenjamin HarrisonGrover ClevelandPreceded byEdward John PhelpsSucceeded byThomas F. Bayard (as Ambassador)35th United States Secretary of WarIn officeMarch 5, 1881 – March 4, 1885PresidentJames ...

Administrative office of the Spanish colonies Portrait of Bartolomé de Las Casas (c.1484 - 1566) Protector of the Indians (Spanish: Protectoría de Los Indios) was an administrative office of the Spanish colonies that deemed themselves responsible for attending to the well-being of the native populations by providing detailed witness accounts of mistreatment in an attempt to relay their struggles and a voice speaking on their behalf in courts, reporting back to the King of Spain.[1] ...

South Korean singer and actor (born 1995) Hwang Min-hyun황민현Hwang in October 2022Born (1995-08-09) August 9, 1995 (age 28)Busan, South KoreaEducationHanyang University Institute for Future Talents[1]Inha University[2]Alma materSchool of Performing Arts Seoul[3]OccupationsSingersongwriteractorMusical careerGenresK-popYears active2012–presentLabelsPledisYMC[a]Swing[a]Formerly ofWanna OneNU'ESTKorean nameHangul황민현Hanja黃旼炫Revise...

Pandangan atas ion kalium (ungu) yang bergerak melintasi saluran kalium (PDB: 1BL8) Saluran kalium adalah jenis saluran ion yang paling terdistribusi secara luas dan pada hakikatnya ditemukan pada semua makhluk hidup.[1] Saluran ini membentuk pori selektif kalium yang membentang pada membran sel. Lebih lanjut, saluran kalium ditemukan pada kebanyakan jenis sel dan mengontrol berbagai fungsi sel yang luas.[2][3] Fungsi Fungsi saluran kalium adalah untuk mengalirk...

蓋爾式手球 蓋爾式手球(英語:Gaelic handball;愛爾蘭語:liathróid láimhe),又稱為愛爾蘭式手球、壁式手球,是一種流行於愛爾蘭的室內球類運動。 蓋爾式手球與被列為奧運項目的手球運動毫無關係,倒是與壁球、短柄牆球極為類似,其差別只是不用球拍,而是徒手擊球。為了避免受傷,球員的雙手均戴上厚皮手套。由於左、右手均可擊球,其戰術相對較為複雜而多變化。...

Jewish community associated with modern-day Ethiopia Not to be confused with the Bene Israel, a Jewish community in India. Ethnic group Beta Israelבֵּיתֶא יִשְׂרָאֵל (Hebrew)ቤተ እስራኤል (Geʽez)Religious ceremony of Ethiopian Jews in Gondar, 1932Total population173,500Regions with significant populations Israel160,500 (2021)[1] Ethiopia12,000 (2021)[2] United States1,000 (2008)[3]LanguagesPredominant:Amharic, ...

Pour les articles homonymes, voir van der Ploeg. Cet article est une ébauche concernant un coureur cycliste australien. Vous pouvez partager vos connaissances en l’améliorant (comment ?). Pour plus d’informations, voyez le projet cyclisme. Paul van der PloegInformationsNaissance 9 novembre 1989 (34 ans)Nationalité australienneÉquipe actuelle State of Matter MAAPSpécialités VTT cross-country, Cross-country eliminatorÉquipes amateurs 2008Felt Bicycles-Sram Components2013Co...

Voce principale: Ballspielverein Borussia 09 Dortmund. Ballspielverein Borussia 09 DortmundStagione 2020-2021Sport calcio Squadra Borussia Dortmund Allenatore Lucien Favre(fino al 13 dicembre) Edin Terzić All. in seconda Manfred Stefes Edin Terzić (fino al 13 dicembre) Presidente Reinhard Rauball Bundesliga3° (in Champions League) DFB-PokalVincitore Supercoppa di GermaniaFinalista Champions LeagueQuarti di finale Maggiori presenzeCampionato: Hummels (33)Totale: Reus (49) Miglior marc...
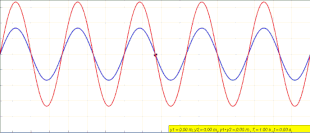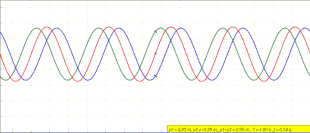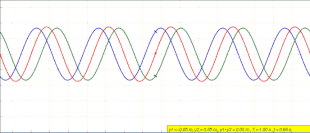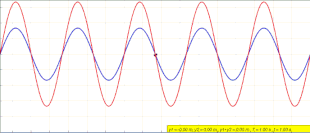
Wave that remains in a constant position Animation of a standing wave (red) created by the superposition of a left traveling (blue) and right traveling (green) wave In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect to time, and the oscillations at different points throughout the wave are in phase. The ...

Map all coordinates using OpenStreetMap Download coordinates as: KML GPX (all coordinates) GPX (primary coordinates) GPX (secondary coordinates) Suburb of Brisbane, Queensland, AustraliaAuchenflowerBrisbane, QueenslandAuchenflower seen from the Brisbane RiverAuchenflowerCoordinates27°28′24″S 152°59′38″E / 27.4733°S 152.9938°E / -27.4733; 152.9938 (Auchenflower (centre of suburb))Population6,053 (2021 census)[1] • Density4,0...

Paula Radcliffe détient plusieurs records nationaux sur piste et sur route. Les records du Royaume-Uni d'athlétisme sont les meilleures performances réalisées par des athlètes britanniques et homologuées par United Kingdom Athletics[1]. Plein air Hommes Épreuve Record Athlète Date Compétition Lieu Réf. 100 m 9 s 83 (+1,3 m/s) Zharnel Hughes 24 juin 2023 New York [2] 200 m 19 s 73 (+1,6 m/s) Zharnel Hughes 23 juillet 2023 Londres [3] 400 m 44 s 26 (AR) Matthe...

2009 television film directed by Michael Feifer The Dog Who Saved ChristmasGenreComedyScreenplay byMichael Ciminera &Richard GnolfoStory byJeffrey SchenckMichael CimineraRichard GnolfoDirected byMichael FeiferStarringMario LopezDean Cain Elisa DonovanSierra McCormick Adrienne Barbeau Gary Valentine Joey DiazMusic byAndres BoultonCountry of originUnited StatesOriginal languageEnglishProductionProducersMichael FeiferJeffrey SchenckCinematographyHank Baumert Jr.EditorsBryan RobertsMatt Stein...