Cone
| |||||||||||||||||||||||||||||
Read other articles:

Artikel ini bukan mengenai Logam alkali. Logam alkali tanah dalam tabel periodik Hidrogen Helium Lithium Berilium Boron Karbon Nitrogen Oksigen Fluor Neon Natrium Magnesium Aluminium Silikon Fosfor Sulfur Clor Argon Potasium Kalsium Skandium Titanium Vanadium Chromium Mangan Besi Cobalt Nikel Tembaga Seng Gallium Germanium Arsen Selen Bromin Kripton Rubidium Strontium Yttrium Zirconium Niobium Molybdenum Technetium Ruthenium Rhodium Palladium Silver Cadmium Indium Tin Antimony Tellurium Iodin...

أويستر باي كوف الإحداثيات 40°51′46″N 73°29′41″W / 40.8628°N 73.4947°W / 40.8628; -73.4947 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة ناسو خصائص جغرافية المساحة 11.018269 كيلومتر مربع11.023176 كيلومتر مربع (1 أبريل 2010) ارتفاع 18 متر ع�...
An environmentally sustainable hotel This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Eco hotel – news · newspapers · books · scholar · JSTOR (September 2014) (Learn how and when to remove this template message) An eco hotel, or a green hotel, is an environmentally sustainable hotel or accommodation that has ...

American filmsby year 1890s 1890–1899 1900s 1900 1901 1902 1903 19041905 1906 1907 1908 1909 1910s 1910 1911 1912 1913 19141915 1916 1917 1918 1919 1920s 1920 1921 1922 1923 19241925 1926 1927 1928 1929 1930s 1930 1931 1932 1933 1934 1935 1936 1937 1938 1939 1940s 1940 1941 1942 1943 19441945 1946 1947 1948 1949 1950s 1950 1951 1952 1953 19541955 1956 1957 1958 1959 1960s 1960 1961 1962 1963 19641965 1966 1967 1968 1969 1970s 1970 1971 1972 1973 19741975 1976 1977 1978 1979 1980s 1980 1981...

Košice-okolie District in the Kosice Region Bohdanovce (Hungarian: Garbócbogdány) is a village and municipality in Košice-okolie District in the Kosice Region of eastern Slovakia. Genealogical resources The records for genealogical research are available at the state archive Statny Archiv in Kosice, Slovakia Reformated church records (births/marriages/deaths): 1728-1899 (parish A) See also List of municipalities and towns in Slovakia External links [1] Surnames of living people in Bohdano...

Dewan Perwakilan Rakyat DaerahKabupaten BimaDewan Perwakilan RakyatKabupaten Bima2019-2024JenisJenisUnikameral Jangka waktu5 tahunSejarahSesi baru dimulai25 September 2019PimpinanKetuaMuhammad Putera Feryandi (Golkar) sejak 18 Oktober 2019[1] Wakil Ketua IMuhammad Aminurlah (PAN) sejak 18 Oktober 2019[1] Wakil Ketua IIYasin (Gerindra) sejak 18 Oktober 2019[1] Wakil Ketua IIIHj. Nurhayati (PPP) sejak 18 Oktober 2019[1] KomposisiAnggota45Partai &a...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مايو 2019) قائد لقوات الصواريخ الاستراتيجية قاراقايف سيرغي معلومات شخصية الميلاد 4 يونيو 1961 (63 سنة) الجنسية روسي الحياة العملية المدرسة الأم الأكاديمية العسكرية ...

Detriti spaziali in un'orbita GEO visti dal polo Componenti di un razzo Delta II caduti in Sudafrica Detriti localizzati su orbite LEO Simulazione di impatto ad alta velocità. Un proiettile a 27 000 chilometri orari colpisce un bersaglio fermo, il flash è generato dalla disintegrazione del proiettile sul bersaglio Con le espressioni detriti spaziali, detriti orbitali, spazzatura spaziale o rottame spaziale si indica tutto ciò che orbita attorno alla Terra, creato dall'uomo e non più ...

British sponge cake Madeira cakeCherry Madeira cake with whipped cream and teaTypeSponge cakeCourseTea or breakfastPlace of originUnited Kingdom Media: Madeira cake Madeira cake is a sponge or butter cake in traditional British and Irish cookery. Origin It is sometimes mistakenly thought to originate from the Madeira Islands. However, that is not the case as it was named after Madeira wine, a Portuguese wine from the islands, which was popular in England in the mid-1800s and was oft...

Place in AndorraEl Pas de la CasaEl Pas de la CasaLocation in AndorraCoordinates: 42°32′32.41″N 1°44′01.78″E / 42.5423361°N 1.7338278°E / 42.5423361; 1.7338278Country AndorraArea • Total17 km2 (7 sq mi)Elevation2,080 m (6,820 ft)Highest elevation2,827 m (9,275 ft)Population (2012) • Total2,996 • Density180/km2 (460/sq mi)ParishEncampWebsitehttp://www.encamp.ad/ El Pas...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

الممثلية النرويجة لدى السلطة الفلسطينية النرويج فلسطين البلد دولة فلسطين السَفير تورون فيزتي الموقع الالكتروني الموقع الرسمي تعديل مصدري - تعديل الممثلية النرويجية لدى السلطة الفلسطينية هي الجهة الدبلوماسية العُليا النرويجية لدى دولة فلسطين، تأسست عام 1999 وي�...

Ahmed Ammi Informasi pribadiNama lengkap Ahmed AmmiTanggal lahir 19 Januari 1981 (umur 43)Tempat lahir Temsaman, MarokoTinggi 1,79 m (5 ft 10+1⁄2 in)Posisi bermain BekInformasi klubKlub saat ini VVV-Venlo (pinjaman dari ADO Den Haag)Nomor 2Karier junior1993–1999 SV Blerick[1]1999–2000 VVVKarier senior*Tahun Tim Tampil (Gol)2001–2007 VVV-Venlo 178 (3)2007–2008 NAC Breda 24 (2)2008– ADO Den Haag 93 (0)2012– → VVV-Venlo (pinjaman) * Penampilan dan...

Part of the Articles of Confederation establishing the United States The Articles of Confederation and Perpetual Union. Part of a series on theAmerican RevolutionDeclaration of Independence (painting)The Committee of Five presents their draft of the Declaration of Independence to the Second Continental Congress in Philadelphia Timeline Military leaders Battles Origins Context Thirteen Colonies Salutary neglect French and Indian War George III Ideas American Enlightenment Republicanism Liberal...

Cette page concerne l'année 2000 (MM en chiffres romains) du calendrier grégorien. Pour l'année 2000 av. J.-C., voir 2000 av. J.-C. Pour le nombre 2000, voir 2000 (nombre). Pour les autres significations, voir 2000 (homonymie). Chronologies Données clés 1997 1998 1999 2000 2001 2002 2003Décennies :1970 1980 1990 2000 2010 2020 2030Siècles :XVIIIe XIXe XXe XXIe XXIIe Chronologies thématiques Art Animation asiatique, Architecture, Arts plas...

هاينكل هي 77معلومات عامةالنوع قاذفة قنابلبلد الأصل ألمانياالمهام قاذفة قنابل استراتيجية التطوير والتصنيعالصانع هاينكلالكمية المصنوعة 1169سيرة الطائرةدخول الخدمة 1942انتهاء الخدمة 1945أول طيران 1939الوضع الحالي منتهية الخدمةالخدمةالمستخدم الأساسي سلاح الجو الألمانيالخصائصا...

33°53′20″N 117°15′36″W / 33.889°N 117.260°W / 33.889; -117.260 Military air base in Riverside County, California Dragon Flight redirects here. For other uses, see dragonflight (disambiguation). March Air Reserve BaseNear Moreno Valley California in the United States of AmericaMarch Air Reserve Base badgeTypeUS Air Reserve BaseSite informationOwnerDepartment of DefenseOperatorUS Air ForceControlled byAir Force Reserve Command (AFRC)ConditionOperati...

Hoogezand-SappemeerStation building in 1973General informationLocationStationsweg 4, Hoogezand, Netherlands[1]Coordinates53°09′34″N 6°46′18″E / 53.15944°N 6.77167°E / 53.15944; 6.77167Operated byNS StationsLine(s)Harlingen–Nieuweschans railwayPlatforms2Tracks2Train operatorsArrivaBus operatorsTaxi de GroothOther informationStation codeHgzHistoryOpened1 May 1868 (1868-05-01)Services Preceding station Arriva Following station Martensh...

Questa voce o sezione sull'argomento artiodattili non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Come leggere il tassoboxOriceClassificazione scientificaDominioEukaryota RegnoAnimalia PhylumChordata ClasseMammalia OrdineArtiodactyla FamigliaBovidae SottofamigliaHippotraginae GenereOryx Specie Oryx beisa Oryx dammah Oryx leucoryx Oryx gazella Gli orici s...

Personal computer by Apple Computer This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Macintosh Quadra 605 – news · newspapers · books · scholar · JSTOR (May...

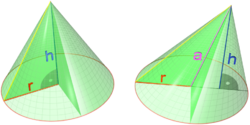






































![{\displaystyle [0,h]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbede90a8f7ff59267c875f09e715c896ce7a51a)












