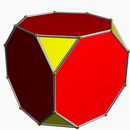
Truncation (geometry)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

1970 film by Claude Chabrol For similarly titled films, see Breach (disambiguation). The BreachDVD coverLa RuptureDirected byClaude ChabrolScreenplay byClaude ChabrolBased onThe Balloon Manby Charlotte ArmstrongProduced byAndré GénovèsStarringStéphane AudranJean-Pierre CasselMichel BouquetAnnie CordyCinematographyJean RabierEdited byJacques GaillardMusic byPierre JansenDistributed byGaumont Film Company (France)New Line Cinema (US)Release date 26 August 1970 (1970-08-26) Ru...

Alfonso VIII dan Ratu Eleanor. Alfonso VIII (11 November 1155 – 5 Oktober 1214), disebut Él de las Navas, adalah Raja Kastilia dari tahun 1158 sampai kematiannya. Ia terkenal karena perannya dalam Reconquista dan jatuhnya Muwahidun. Setelah kalah besar dengan pasukannya sendiri dalam pertempuran Alarcos melawan Muwahidun, ia memimpin koalisi pangeran Kristen dan tentara salib yang menghancurkan kekuatan Muwahidun dalam pertempuran Navas de Tolosa tahun 1212, yang menandai tib...

AACTA AwardsPenghargaan terkini: AACTA Awards ke-8DeskripsiUntuk mengakui dan menghormati prestasi menonjol dalam industri film dan televisi Australia.[1]NegaraAustraliaDipersembahkan olehAustralian Academy of Cinema and Television Arts (AACTA)Diberikan perdana1958 (untuk menghormati prestasi 1957/1958)Situs webhttp://www.aacta.orgSiaran televisi/radioSaluranABC (1977, 1980–1983, 1986–1987, 1989–1990, 1993, 1995, 1997, 2003–2004)SBS (1998–2000)Seven Network (1978, 2001, 2016...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Shenzhen Airlines – berita · surat kabar · buku · cendekiawan · JSTOR Shenzhen Airlines深圳航空公司 IATA ICAO Kode panggil ZH CSZ SHENZHEN AIR DidirikanNovember 1992Mulai beroperasi17 September 199...

Union Army atau Tentara Federal adalah pasukan darat yang bertarung untuk Union pada masa Perang Saudara Amerika dari 1861 sampai 1865. Ini meliputi tentara reguler permanen Amerika Serikat, yang dipadukan dengan sejumlah besar unit temporer yang terdiri dari para sukarelawan dan wajib militer. Union Army bertarung dan mengalahkan Confederate Army pada masa perang tersebut. Sekitar dua juta dan mungkin dua setengah juta orang bertugas dalam Union Army; hampir seluruhnya (lebih dari 94%) adala...

Italian footballer Thomas Manfredini Manfredinin with Atalanta in 2010Personal informationDate of birth (1980-05-27) 27 May 1980 (age 43)Place of birth Ferrara, ItalyHeight 1.80 m (5 ft 11 in)Position(s) Centre-backTeam informationCurrent team SP La Fiorita (manager)Senior career*Years Team Apps (Gls)1997–1999 SPAL 14 (0)1999–2005 Udinese 64 (2)2004 → Fiorentina (loan) 11 (0)2004–2005 → Catania (loan) 30 (3)2005–2013 Atalanta 134 (4)2005–2006 → Rimini (loan...

Ne doit pas être confondu avec Slovaquie ou Slavonie. République de Slovénie(sl) Republika Slovenija(it) Repubblica di Slovenia (hu) Szlovén Köztársaság Drapeau de la Slovénie Armoiries de la Slovénie Hymne en slovène : Zdravljica (« Je lève mon verre ») Fête nationale 25 juin · Événement commémoré Proclamation d'indépendance vis-à-vis de la Yougoslavie (1991) La république de Slovénie en Europe (l'Union européenne en vert clair...

OrganelRincianPelafalan/ɔːrɡəˈnɛl/Bagian dariSelPengidentifikasiBahasa LatinorganellaMeSHD015388THH1.00.01.0.00009FMA63832Daftar istilah mikroanatomi[sunting di Wikidata] Dalam biologi sel, organel adalah subunit khusus, biasanya di dalam sel, yang memiliki fungsi tertentu. Nama organel berasal dari gagasan bahwa struktur ini adalah bagian dari sel, seperti halnya organ bagi tubuh. Akhirnya, nama yang diberikan adalah organel, dengan akhiran -el yang menjelaskan sifat diminutif (kec...

Painting by Pablo Picasso Girl in a ChemiseArtistPablo PicassoYearc.1905Mediumoil on canvasDimensions72.7 cm × 60 cm (28.6 in × 24 in)LocationTate Girl in a Chemise (French: Jeune femme en chemise) is an oil-on-canvas painting created c. 1905 by Pablo Picasso. It is a portrait of a girl, whom experts believe to be Madeleine, Picasso's girlfriend during this period. Stylistically, the painting belongs to Picasso's Rose Period, although it is predomin...

Robert FiskRobert Fisk di Al Jazeera Forum 2010Lahir(1946-07-12)12 Juli 1946Maidstone, Kent, InggrisMeninggal30 Oktober 2020(2020-10-30) (umur 74)Dublin, IrlandiaWarga negara Irlandia Inggris Pendidikan Universitas Lancaster (BA, 1968) Trinity College Dublin (PhD, 1985) PekerjaanKoresponden Timur Tengah untuk The IndependentKarya terkenal Jacob's Award Amnesty International UK Press Awards British Press Awards International Journalist of the Year Lannan Cultural Freedom Prize Suami/istr...

Chika JessicaLahirSisca Jessica25 April 1988 (umur 36)Bandung, Jawa Barat, IndonesiaKebangsaanIndonesiaNama lainChika JessicaPekerjaanPemeranpresenterkomedianTahun aktif2007—sekarang Sisca Jessica (lahir 25 April 1988), lebih dikenal sebagai Chika Jessica adalah pemeran, presenter dan komedian Indonesia. Filmografi Film Tahun Judul Peran Catatan Ref. 2009 Merantau Astri 2012 Bangkit dari Kubur Trisna 2012 Dendam dari Kuburan Poppy 2013 Get M4rried Cewek alay Slank Nggak Ada ...

习近平 习近平自2012年出任中共中央总书记成为最高领导人期间,因其废除国家主席任期限制、开启总书记第三任期、集权统治、公共政策与理念、知识水平和自述经历等争议,被中国大陸及其他地区的民众以其争议事件、个人特征及姓名谐音创作负面称呼,用以恶搞、讽刺或批评习近平。对习近平的相关负面称呼在互联网上已经形成了一种活跃、独特的辱包亚文化。 权力�...

Lullington HeathSite of Special Scientific InterestLocationEast SussexGrid referenceTQ 543 017[1]InterestBiologicalArea72.7 hectares (180 acres)[1]Notification1986[1]Location mapMagic Map Lullington Heath is a 72.7-hectare (180-acre) biological Site of Special Scientific Interest west of Eastbourne in East Sussex.[1][2] It is a national nature reserve[3] and a Nature Conservation Review site, Grade I.[4] This site has two nationally unc...

1918 peace treaty during World War I Not to be confused with the contemporaneous Treaty of Brest-Litovsk between Russia and the Central Powers. Treaty of Brest-Litovsk(9 February 1918)BrotfriedenБерестейський мирSigning of the Peace Treaty of Brest-Litovsk during the night of 9-10 February 1918. Sitting in the middle from the left: Count Ottokar Czernin, Richard von Kühlmann and Vasil RadoslavovSigned9 February 1918LocationBrest-Litovsk, Grodno Governorate (German occupation)...

Diagram tangga dari rangkaian Monostable Multivibrator Logika tangga (Ladder logic) adalah bahasa pemrograman yang dipakai untuk menggambarkan secara grafis diagram rangkaian elektronika dan perangkat keras komputer berdasarkan logika berbasis-relay yang banyak dijumpai pada aplikasi Programmable Logic Controllers (PLC) dan kendali industri. Sesuai dengan namanya, program ini menggunakan gambar anak tangga yang terdiri dari garis-garis tegak dan garis mendatar untuk menyajikan fungsi logika r...

Rosemarie Wetzel (lahir 20 Januari 1976) adalah model internasional asal Belanda yang pernah populer pada dekade 1990-an. Rosemarie pertama kali bekerja untuk agen Factory Models di Amsterdam sewaktu bekerja sebagai asisten dokter. Selanjutnya ia masuk dalam jaringan Elite Model dan beralih ke Paris. Ia banyak terlibat dalam sesi foto untuk iklan, peragaan busana, dan penerbitan pada paruh akhir dekade 90-an. Semenjak tahun 2000 namanya menghilang, karena ia memutuskan untuk fokus pada keluar...

Cet article concerne un métier artistique. Pour le recueil, voir Parolier (recueil). Cet article est une ébauche concernant la musique, l’art et un métier. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Jean Baptiste Clément photographié par Nadar. Un parolier, ou une parolière, écrit le texte d'une chanson, la mélodie étant l'œuvre du compositeur, ou du beatmaker. L'antériorité des paroles ou...

Argentina en los Juegos Olímpicos Bandera de ArgentinaCódigo COI ARGCON Comité Olímpico Argentino.Juegos Olímpicos de Pekín 2008Deportistas 138 (80 hombres y 58 mujeres) en 19 deportesAbanderado Apertura: Emanuel GinóbiliCierre: Juan CuruchetMedallasPuesto: 34 de 204 2 0 4 6 Historia olímpicaJuegos de verano 1900 • 1904 • 1908 • 1912 • 1920 • 1924 • 1928 • 1932 • 1936 • 1948 &#...

Tower and palace structure in the Alhambra of Granada Exterior view of the tower The Torre de la Cautiva (Spanish: Torre de la Cautiva, lit. 'tower of the captive [woman]') is a tower in the walls of the Alhambra in Granada, Spain. It is one of several towers along the Alhambra's northern wall which were converted into a small palatial residence in the 14th century. It is considered an exceptional example of Nasrid domestic architecture from this period.[1]: 19...

2002 album by Circus Devils The Harold Pig MemorialStudio album by Circus DevilsReleased2002GenreAlternative rock, psychedelic rockLabelRockathon Records /the Fading Captain SeriesProducerTodd TobiasCircus Devils chronology Ringworm Interiors(2001) The Harold Pig Memorial(2002) Pinball Mars(2003) Professional ratingsReview scoresSourceRatingAllmusic[1]Popmatters[2]The Broken Face The Harold Pig Memorial is the second studio album by the American psychedelic rock trio Circu...