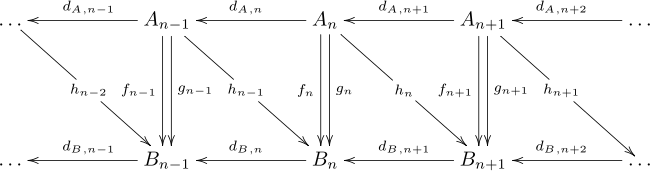
Chain complex
|
Read other articles:

American college football season 2022 Nebraska Cornhuskers footballConferenceBig Ten ConferenceDivisionWestRecord4–8 (3–6 Big Ten)Head coachScott Frost (5th season; first three games)Mickey Joseph (interim; remainder of season)Offensive coordinatorMark Whipple (1st season)Offensive schemeSpreadDefensive coordinatorErik Chinander (5th season; first four games)Bill Busch (interim; remainder of season)Base defense4–3Home stadiumMemorial Stadium(capacity: 8...

Distrito histórico de MacFarlane Homestead(MacFarlane Homestead Historic District)Registro Nacional de Lugares Históricos Distrito Histórico Distrito histórico de MacFarlane HomesteadUbicación Distrito histórico de MacFarlane Homestead Ubicación en MiamiCoordenadas 25°43′40″N 80°15′32″O / 25.727778, -80.258889Dirección Jefferson Street, Frow Avenue, Brooker Street, y Grand AvenueUbicación Coral Gables FloridaCondado (s) Miami-DadeDatos generalesAgregado...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Steady Nerves – news · newspapers · books · scholar · JSTOR (May 2021) (Learn how and when to remove this template message) 1985 studio album by Graham Parker and the ShotSteady NervesStudio album by Graham Parker and the ShotReleased1985GenreRockLabelE...

Greek/Danish princess (1914–2001) For the queen consort of Spain sometimes known as Sophia of Greece and Denmark, see Queen Sofía of Spain. Sophie of Greece and DenmarkPrincess Christoph of HessePrincess George William of HanoverPrincess Sophie in 1922Born(1914-06-26)26 June 1914Mon Repos, Corfu, Kingdom of GreeceDied24 November 2001(2001-11-24) (aged 87)Schliersee, Bavaria, GermanyBurial30 November 2001Schliersee, Bavaria, GermanySpouse Prince Christoph of Hesse &#...

Selina Graf (2022) Selina Graf (* 1994 in Salzburg) ist eine österreichische Schauspielerin.[1] Bekannt wurde Graf durch die ORF-Serie Walking on Sunshine, in der sie Conny Ulrich verkörpert.[2] Inhaltsverzeichnis 1 Leben 2 Theater 3 Filmografie 4 Weblinks 5 Einzelnachweise Leben Selina Graf besuchte die Übungsvolksschule in Nonntal und legte am Bundesgymnasium Nonntal die Matura ab. Anschließend studierte sie in Salzburg Mathematik. Von 2015 bis 2019 absolvierte sie ihr S...

Sebuah pesan anti-FGM yang disampaikan oleh Asosiasi Keluarga Berencana Uganda di dekat Kapchorwa, Uganda, 2004. Di plakat tersebut tertulis Hentikan sunat perempuan. Berbahaya untuk kesehatan wanita.DefinisiDidefinisikan pada tahun 1977 oleh WHO, UNICEF, dan UNFPA sebagai penghilangan sebagian atau seluruh bagian luar kelamin wanita atau perlukaan lainnya pada organ kelamin wanita untuk alasan nonmedis.[1]AreaAfrika, Asia Tenggara, Timur Tengah, dan pada berbagai komunitas di area in...

Para Koribantes yang sedang menari. Koribantes (bahasa Yunani: Κορύβαντες) adalah para penari yang memuja dewi Kibele dari Frigia dengan musik dan tarian. Mereka disebut juga Kourbantes di Frigia. Koribantes diasosiasikan dengan Kouretes, sembilan orang penari yang memuliakan Rea, dewa padanan Kibele dari Kreta dan ibu para dewa. Para Kuretes adalah para penari yang menjaga Zeus semasa bayi. Para Koribantes menari dengan memakai baju perang, mereka menyesuaikan irama musik denga...

Arum tutul putih Status konservasi Risiko Rendah (IUCN 3.1)[1] Klasifikasi ilmiah Domain: Eukaryota Kerajaan: Plantae Upakerajaan: Trachaeophyta Divisi: Magnoliophyta Kelas: Liliopsida Ordo: Alismatales Famili: Araceae Genus: Zantedeschia Spesies: Zantedeschia albomaculata(Hook.) Baill. Arum tutul putih (Zantedeschia albomaculata; sinonim: Calla albomaculata; bahasa Inggris: calla lily) adalah terna sejati (perennial herb) dan termasuk ke dalam keluarga Araceae. Tumbuhan ini dite...

Gothic Novel by Ann Radcliffe This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: A Sicilian Romance – news · newspapers · books · scholar · JSTOR (October 2016) A Sicilian Romance Title page to the 1792 editionAuthorAnn RadcliffeCountryUnited KingdomLanguageEnglishGenre Gothic Horror Romance Published...

Province of Afghanistan Province in AfghanistanKandahar کندهارProvinceFrom the top, Panjwayi District, Kandahar University, Dahla DamNickname: Loy kandaharMap of Afghanistan with Kandahar highlightedCoordinates (Capital): 31°00′N 65°30′E / 31.0°N 65.5°E / 31.0; 65.5Country AfghanistanCapitalKandaharGovernment • TypeProvince • BodyUlema Council[1] • GovernorMullah Shirin Akhund[2] •&#...

2022 attacks in Moldova's breakaway region of Transnistria 2022 Transnistria attacksPart of the Transnistria conflict and spillover of the Russian invasion of UkraineFront of the damaged building of the Ministry of State SecurityLocationCobasna, Maiac, Tiraspol, Vărăncău and Vladimirovca, in TransnistriaDate25–27 April, 6 May and 5 June 2022Target Ministry of State Security Tiraspol Airport Grigoriopol transmitter Cobasna ammunition depot Former aerodrome in Vărăncău Military reserve ...

Lembah Sorik MarapiKecamatanPeta lokasi Kecamatan Lembah Sorik MarapiNegara IndonesiaProvinsiSumatera UtaraKabupatenMandailing NatalPemerintahan • Camat-Populasi • Total- jiwaKode Kemendagri12.13.09 Kode BPS1202033 Luas- km²Desa/kelurahan8/1 Lembah Sorik Marapi adalah sebuah kecamatan di Kabupaten Mandailing Natal, Sumatera Utara, Indonesia.[1] Referensi ^ Salinan arsip. Diarsipkan dari versi asli tanggal 2017-09-30. Diakses tanggal 2015-08-17. lbsK...

Owen Wingrave Op. 85 Monumento en memoria de Benjamin BrittenGénero ÓperaActos 2 actosAmbientada en LondresBasado en un cuento de Henry JamesPublicaciónAño de publicación siglo XXIdioma InglésMúsicaCompositor Benjamin BrittenPuesta en escenaLugar de estreno BBCFecha de estreno 16 de mayo de 1971Personajes véase PersonajesLibretista Myfanwy Piper[editar datos en Wikidata] Owen Wingrave es una ópera en dos actos con música de Benjamin Britten, su Opus 85, y libreto en inglé...

Sri Lankan sprinter Ajith PremakumaraPremakumara at the 2017 Asian ChampionshipsPersonal informationBorn12 October 1991 (1991-10-12) (age 32)[1]Sri Lanka[2]Height168 cm (5 ft 6 in)[2]Weight77 kg (170 lb)SportSportAthleticsEvent(s)200 m, 400 mAchievements and titlesPersonal best(s)200 m – 21.35 (2017)400 m – 46.36 (2017)[1] Medal record Representing Sri Lanka Asian Athletics Championships 2017 Bhubaneswar Men's 4×400...

Fyodor StepunBornFyodor Avgustovich Stepun(1884-02-18)18 February 1884Moscow, Russian EmpireDied23 February 1965(1965-02-23) (aged 81)Munich, West GermanyOccupationphilosopherhistorianmemoiristNationalityRussian, GermanSwede, LithuanianCitizenshipRussian, GermanGenrephilosophysociologyLiterary movementneo-Kantism[1] Fyodor Avgustovich Stepun (Russian: Фёдор А́вгустович Степу́н; February 18, 1884 – February 23, 1965) (also known as Friedrich Steppuhn) was ...

Flemish portrait painter Self-portrait, 1681 Jacob Ferdinand Voet or Jakob Ferdinand Voet[1] (c. 1639 – 26 September 1689) was a Flemish portrait painter.[2] He had an international career that brought him to Italy and France, where he made portraits for an elite clientele. Voet is regarded as one of the best and most fashionable portrait painters of the High Baroque.[3] Life Portrait of a Gentleman with a Lace Collar, c. 1660-1670 Few details about Voet...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: G381/382 Beijing-Harbin Through Train – news · newspapers · books · scholar · JSTOR (October 2015) (Learn how and when to remove this template message) G381 prior to departure at Beijing South railway station. The G381/382 Beijing-Harbin Through Train (Chinese: G381/382次�...

Mosque in Kuala Lumpur, Malaysia 3°8′56.06″N 101°41′45.46″E / 3.1489056°N 101.6959611°E / 3.1489056; 101.6959611 مسجد جامع سلطان عبدالصمدSultan Abdul Samad Jamek MosqueMasjid Jamek Sultan Abdul Samad (Malay)Jamek Mosque, also known as Friday Mosque, is recognised as the oldest Islamic place of worship in Kuala LumpurReligionAffiliationIslamLeadershipImam(s): Ustaz Haji Yahya Mahyuddin bin Datuk Haji Utoh Said (2017–present)Locati...

Airport serving Panama City, Florida, United States This article is about the current airport open since 2010. For the previous airport serving Panama City, Florida, see Panama City–Bay County International Airport. Northwest Florida Beaches International AirportIATA: ECPICAO: KECPFAA LID: ECPSummaryAirport typePublicOwnerPanama City-Bay County Airport and Industrial DistrictServesPanama City / Panama City BeachLocationBay County, FloridaOpenedMay 23, 2010; 13 years ago (2...

Western AustraliaAustralian Senate Show map of Australia Show map of Western AustraliaCreated1901Party Labor (5) Liberal (5) Greens (2) This is a list of senators from the state of Western Australia since Australian Federation in 1901. List Senate Election Senator(Party) Senator(Party) Senator(Party) Senator(Party) Senator(Party) Senator(Party) Senator(Party) Senator(Party) Senator(Party) Senator(Party) Senator(Party) Senator(Party) 1901–1903 1901 Edward Harney(Free Tra...














![{\displaystyle \partial _{n}:\,(\sigma :[v_{0},\ldots ,v_{n}]\to X)\mapsto (\sum _{i=0}^{n}(-1)^{i}\sigma :[v_{0},\ldots ,{\hat {v}}_{i},\ldots ,v_{n}]\to X)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d64d20dabc262201e2da3e8e282cd1e6c2a46ce)












