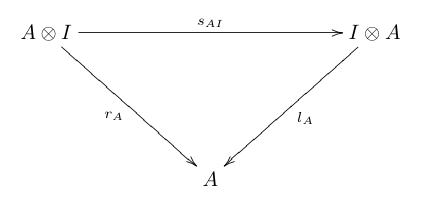
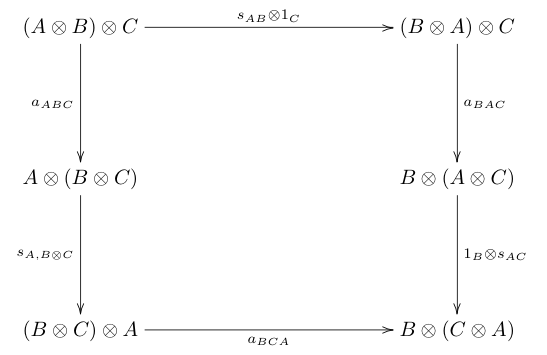
Symmetric monoidal category

In category theory, a branch of mathematics, a symmetric monoidal category is a monoidal category (i.e. a category in which a "tensor product" $\otimes$ is defined) such that the tensor product is symmetric (i.e. $A\otimes B$ is, in a certain strict sense, naturally isomorphic to $B\otimes A$ for all objects $A$ and $B$ of the category). One of the prototypical examples of a symmetric monoidal category is the category of vector spaces over some fixed field k, using the ordinary tensor product of vector spaces.

Definition

A symmetric monoidal category is a monoidal category (C, ⊗, I) such that, for every pair A, B of objects in C, there is an isomorphism $s_{AB}:A\otimes B\to B\otimes A$ called the swap map^[1] that is natural in both A and B and such that the following diagrams commute:

The unit coherence:
The associativity coherence:
The inverse law:

In the diagrams above, a, l, and r are the associativity isomorphism, the left unit isomorphism, and the right unit isomorphism respectively.

Examples

Some examples and non-examples of symmetric monoidal categories:

The category of sets. The tensor product is the set theoretic cartesian product, and any singleton can be fixed as the unit object.
The category of groups. Like before, the tensor product is just the cartesian product of groups, and the trivial group is the unit object.
More generally, any category with finite products, that is, a cartesian monoidal category, is symmetric monoidal. The tensor product is the direct product of objects, and any terminal object (empty product) is the unit object.
The category of bimodules over a ring R is monoidal (using the ordinary tensor product of modules), but not necessarily symmetric. If R is commutative, the category of left R-modules is symmetric monoidal. The latter example class includes the category of all vector spaces over a given field.
Given a field k and a group (or a Lie algebra over k), the category of all k-linear representations of the group (or of the Lie algebra) is a symmetric monoidal category. Here the standard tensor product of representations is used.
The categories (Ste, $\circledast$ ) and (Ste, $\odot$ ) of stereotype spaces over ${\mathbb {C} }$ are symmetric monoidal, and moreover, (Ste, $\circledast$ ) is a closed symmetric monoidal category with the internal hom-functor $\oslash$ .

Properties

The classifying space (geometric realization of the nerve) of a symmetric monoidal category is an $E_{\infty }$ space, so its group completion is an infinite loop space.^[2]

Specializations

A dagger symmetric monoidal category is a symmetric monoidal category with a compatible dagger structure.

A cosmos is a complete cocomplete closed symmetric monoidal category.

Generalizations

In a symmetric monoidal category, the natural isomorphisms $s_{AB}:A\otimes B\to B\otimes A$ are their own inverses in the sense that $s_{BA}\circ s_{AB}=1_{A\otimes B}$ . If we abandon this requirement (but still require that $A\otimes B$ be naturally isomorphic to $B\otimes A$ ), we obtain the more general notion of a braided monoidal category.

References

^ Fong, Brendan; Spivak, David I. (2018-10-12). "Seven Sketches in Compositionality: An Invitation to Applied Category Theory". arXiv:1803.05316 [math.CT].
^ Thomason, R.W. (1995). "Symmetric Monoidal Categories Model all Connective Spectra" (PDF). Theory and Applications of Categories. 1 (5): 78–118. CiteSeerX 10.1.1.501.2534.

Symmetric monoidal category at the nLab
This article incorporates material from Symmetric monoidal category on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

Category theory

Key concepts

Universal constructions

Limits	Terminal objects Products Equalizers Kernels Pullbacks Inverse limit
Colimits	Initial objects Coproducts Coequalizers Cokernels and quotients Pushout Direct limit

Algebraic categories

Constructions on categories

Higher category theory

Key concepts

Categorification

Enriched category

Higher-dimensional algebra

n-categories

Weak `n`-categories	Bicategory (pseudofunctor) Tricategory Tetracategory Kan complex ∞-groupoid ∞-topos
Strict `n`-categories	2-category (2-functor) 3-category

Categorified concepts

Read other articles:

Đổi Mới

Bagian dari seriSosialisme Perkembangan Sejarah sosialisme Perdebatan kalkulasi sosialis Ekonomi sosialis Gagasan Penghitungan dalam barang Kepemilikan kolektif Koperasi Kepemilikan bersama Demokrasi ekonomi Perencanaan ekonomi Kesetaraan kesempatan Asosiasi bebas Demokrasi industri Model masukan-keluaran Internasionalisme Kupon kerja Keseimbangan material Ekonomi sejawat ke sejawat(Ekonomi berbagi) Produksi untuk penggunaan Kepemilikan negara Manajemen mandiri Dividen sosial Kepemilikan sosi...

Liberalisme republik

Liberalisme republik adalah sebuah teori hubungan internasional yang mengklaim bahwa negara-negara demokrasi liberal lebih damai daripada negara lain. Hal ini bisa dijelaskan sebagai hasil dari kesamaan budaya politik dalam negeri, nilai moral bersama, kerja sama ekonomi, dan saling ketergantungan (interdependensi).[1] Lihat pula Teori perdamaian liberal Internasionalisme liberal Referensi ^ Jackson, Robert and Georg Sorensen (2006), Introduction to International Relations:theories an...

Niger

Disambiguazione – Se stai cercando altri significati, vedi Niger (disambigua). Questa voce o sezione tratta di eventi in corso o di immediata attualità. Le informazioni possono pertanto cambiare rapidamente con il progredire degli eventi. Se vuoi scrivere un articolo giornalistico sull'argomento, puoi farlo su Wikinotizie. Non aggiungere speculazioni alla voce. Niger (dettagli) (dettagli) (FR) Unité - Travail - Progrès(IT) Unità - Lavoro - Progresso Niger - Localizzazione Dati amminist...

Lilí Álvarez

Spanish tennis player Lilí ÁlvarezLilí Álvarez at the 1926 Wimbledon Championships ladies finalFull nameElia Maria González-Álvarez y López-ChicheriCountry (sports)Spain (−1936)France (1936–)[1]Born(1905-05-09)9 May 1905Rome, ItalyDied8 July 1998(1998-07-08) (aged 93)Madrid, SpainPlaysRight-handedSinglesHighest rankingNo. 2 (1927, A. Wallis Myers)[2]Grand Slam singles resultsFrench OpenSF (1930, 1931, 1936, 1937)WimbledonF (1926, 1927, 1928)...

Kalenderhane Mosque

Mosque in Istanbul, Turkey Kalenderhane MosqueThe Mosque viewed from the southeast in 2012ReligionAffiliationSunni IslamYear consecrated1746LocationLocationIstanbul, TurkeyLocation in the Fatih district of IstanbulGeographic coordinates41°00′47″N 28°57′37″E / 41.013132°N 28.960304°E / 41.013132; 28.960304ArchitectureTypeChurch with Greek cross planStyleMiddle Byzantine - ComnenianCompleted12th centuryMinaret(s)1 Dome of the mosque Kalenderhane Mosque (Turki...

Himpunan Mahasiswa Islam

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Himpunan Mahasiswa Islam – berita · surat kabar · buku · cendekiawan · JSTOR Himpunan Mahasiswa IslamLambang Himpunan Mahasiswa IslamSingkatanHMITanggal pendirian5 Februari 1947; 77 tahun lalu (1947-02-0...

Software patents under the European Patent Convention

Computer programs, software and patent law Topics Software patent Debate Free software List of patents Treaties TRIPS Agreement Patent Cooperation Treaty European Patent Convention Countries Canada United Kingdom United States Case law European Patent Office United Kingdom Related topics Business methods vte The patentability of software, computer programs and computer-implemented inventions under the European Patent Convention (EPC) is the extent to which subject matter in these fields is p...

Shirley Ardell Mason

Shirley Ardell MasonShirley Ardell MasonLahir(1923-01-25)25 Januari 1923Meninggal26 Februari 1998(1998-02-26) (umur 75)Kebangsaan AmericanNama lainSybil Isabel DorsettDikenal atasOrang dengan pemecahan kepribadian Shirley Ardell Mason (Dodge Center, Minnesota, 25 Januari 1923 – 26 Februari 1998), adalah seorang wanita yang kehidupannya didokumentasikan di buku dan film dengan nama Sybil Isabel Dorsett untuk melindungi identitas aslinya. Buku itu ditulis oleh Flora Rheta Schr...

Человек прямоходящий

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Paus Benediktus XVI

PausBenediktus XVIUskup RomaPaus Benediktus XVI pada tahun 2010GerejaGereja Katolik RomaAwal masa jabatan19 April 2005Masa jabatan berakhir28 Februari 2013PendahuluYohanes Paulus IIPenerusFransiskusImamatTahbisan imam29 Juni 1951oleh Michael von FaulhaberTahbisan uskup28 Mei 1977oleh Josef StanglPelantikan kardinal27 Juni 1977oleh Paus Paulus VIInformasi pribadiNama lahirJoseph Aloisius RatzingerLahir(1927-04-16)16 April 1927Marktl, Bavaria, Reich JermanWafat31 Desember 2022(2022-12...

The Roanoke Times

Newspaper in Roanoke, Virginia The Roanoke TimesThe July 27, 2005 front page ofThe Roanoke TimesTypeDaily newspaperFormatBroadsheetOwner(s)Lee EnterprisesPublisherSamuel WorthingtonFounded1886LanguageEnglishHeadquarters2l0 Church Ave SW Suite 100Roanoke, Virginia 24011 United StatesCirculation19,657 Daily 22,103 Sunday (as of 2023)[1]Websiteroanoke.com The Roanoke Times is the primary newspaper in Southwestern Virginia and is based in Roanoke, Virginia, United States. It is p...

Proventus

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Proventus – news · newspapers · books · scholar · JSTOR (December 2007) (Learn how and when to remove this ...

14 липня

← липень → Пн Вт Ср Чт Пт Сб Нд 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 2024 рік 14 липня — 195-й день року (196-й у високосні роки) в григоріанському календарі. До кінця року залишається 170 днів. Цей день в історії: 13 липня—14 липня—15 липня Зміст 1 Свята...

List of ministers of foreign affairs of Cyprus

This is a list of ministers of foreign affairs of the Republic of Cyprus since the independence in 1960: Image Minister Began Ended Spyros Kyprianou 16 August 1960 15 June 1972 Ioannis Christophides 16 June 1972 8 March 1978 Nicos A. Rolandis 3 March 1978 21 September 1983 Georgios Iacovou 22 September 1983 27 February 1993 Alekos Michaelides 28 February 1993 8 April 1997 Ioannis Kasoulidis 9 April 1997 28 February 2003 Georgios Iacovou 1 March 2003 12 June 2006 Giorgos Lillikas 13 June 2006...

皮拉图巴

皮拉图巴Piratuba市镇皮拉图巴在巴西的位置坐标：27°25′12″S 51°46′19″W / 27.42°S 51.7719°W / -27.42; -51.7719国家巴西州圣卡塔琳娜州面积 • 总计145.701 平方公里（56.255 平方英里）海拔430 公尺（1,410 英尺）人口（2007） • 總計4,570人 • 密度31.4人/平方公里（81.2人/平方英里）皮拉图巴（葡萄牙语：Piratuba）是巴西圣卡塔琳�...

Monogatari

Para la serie de novelas escritas por Nisio Isin, véase Monogatari (serie). Este artículo o sección necesita referencias que aparezcan en una publicación acreditada. Busca fuentes: «Monogatari» – noticias · libros · académico · imágenesEste aviso fue puesto el 24 de diciembre de 2013. Murasaki Shikibu, El cuento de Genji (Tee Tae de Genji) El monogatari (物語, monogatari?) es un género de la literatura de Japón. Es una narrativa en prosa de gran extensión...

Borgo (rione di Roma)

R. XIV BorgoStemma ufficiale Il rione e la Città del Vaticano visti da Castel Sant'Angelo Stato Italia Regione Lazio Provincia Roma Città Roma Capitale CircoscrizioneMunicipio Roma I Data istituzione1586 Codice114 Superficie0,49 km² Abitanti2 728 ab. Densità5 593,6 ab./km² Mappa dei quartieri di {{{comuneMappa}}} Borgo, talvolta chiamato I Borghi, è il quattordicesimo rione di Roma, indicato con R. XIV. Indice 1 Geografia fisica 1.1 Territorio 2 Storia 2.1 L'et�...

يان زفيهليك

يان زفيهليك معلومات شخصية الميلاد 17 يناير 1950 (العمر 74 سنة) مركز اللعب مهاجم الجنسية سلوفاكيا المسيرة الاحترافية1 سنوات فريق م. (هـ.) 1969–1976 سلوفان براتيسلافا 1976–1977 دوكلا براغ 1977–1982 سلوفان براتيسلافا 1982–1983 هاسيلت المنتخب الوطني 1974–1979 تشيكوسلوفاكيا 17 (4) الفرق التي دربها...

Vladislav Tretiak

Vladislav Tretiak Información personalApodo Русская стена Nacimiento 25 de abril de 1952 (72 años)Orudyevo (Rusia) Nacionalidad Rusa y soviéticaReligión Iglesia ortodoxa Características físicasAltura 1,85 m Peso 79 kg EducaciónEducado en Moscow State Academy of Physical Culture Información profesionalOcupación Jugador de hockey sobre hielo y político Cargos ocupados Diputado de RusiaDiputado de RusiaDiputado de RusiaDiputado de Rusia (2003-2007)Diputado de...

Soneta Volume 11 - Indonesia (album)

artikel ini tidak memiliki pranala ke artikel lain. Tidak ada alasan yang diberikan. Bantu kami untuk mengembangkannya dengan memberikan pranala ke artikel lain secukupnya. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Artikel in...