Aryabhatiya
|
Read other articles:
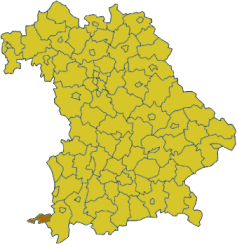
Lindau Bản đồ của Bavaria với huyện Lindau Bang Bayern Vùng hành chính Swabia Vùng Allgäu Thủ phủ Lindau Diện tích 323 km² Dân số 77.100 (2000) Mật độ 238 /km² Mã biển số xe LI Trang mạng landkreis-lindau.de Lindau là một huyện (Landkreis) ở bang Bayern, Đức; thủ phủ là thành phố Lindau. Các đơn vị giáp ranh (từ phía đông theo chiều kim đồng hồ) là: Oberallgäu, Áo (bang Vorarlberg), hồ Constance và bang Baden-W�...

Kirche Saint-Pierre und Friedhof Innenraum Die katholische Kirche Saint-Pierre in Saint-Pierre-les-Églises, einem Ortsteil von Chauvigny im Département Vienne in der französischen Region Nouvelle-Aquitaine, ist im Kern ein vorromanischer Kirchenbau, der wahrscheinlich auf eine merowingische Vorgängerkirche zurückgeht. Im 19. Jahrhundert wurden in der Kirche Wandmalereien entdeckt, die in karolingische Zeit datiert werden und die zu den ältesten in Europa zählen. Im Jahr 1952 wurde die ...

Para otros usos de este término, véase Doncellas del Rin. Rheintochter R1 Tipo Misil antiaéreo (SAM)Historia de servicioEn servicio No llegó a entrar en servicioHistoria de producciónFabricante Rheinmetall-BorsigEspecificacionesPeso 1.748 kgLongitud 10,3 mOjiva Cabeza explosiva de 136 kg. Espoleta de proximidad acústica Kranich.Motor motor cohete de combustible sólido de dos etapasEnvergadura 2,65 mAltitud 8 kmVelocidad máxima 485 m/sSistema de guía MCLOS. El cohete tenía bengalas i...

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Masalah khususnya adalah: terlalu singkat Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saa...

Japanese security company You can help expand this article with text translated from the corresponding article in Japanese. Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Consider adding a topic to this template: th...

Dolní Žandov Dolní Žandov (Tschechien) Basisdaten Staat: Tschechien Tschechien Region: Karlovarský kraj Bezirk: Cheb Fläche: 4133,4611[1] ha Geographische Lage: 50° 1′ N, 12° 33′ O50.01694444444412.546388888889540Koordinaten: 50° 1′ 1″ N, 12° 32′ 47″ O Höhe: 540 m n.m. Einwohner: 1.222 (1. Jan. 2023)[2] Postleitzahl: 354 93 Kfz-Kennzeichen: K (alte CH) Verkehr Bahnanschluss: Plzeň–Cheb S...

Battle in the 2022 Russian invasion of Ukraine For other military conflicts involving Odesa, see Battle of Odesa. Odesa strikesPart of the Russian invasion of UkraineAftermath of a Russian missile strike against warehouses in Odesa on 24 FebruaryDate24 February 2022 (2022-02-24) – present(1 year, 9 months, 1 week and 6 days)LocationOdesa, Odesa Oblast, UkraineBelligerents Russia UkraineUnits involved Russian Armed Forces Russian Air ...

Andrés el Apóstol en un vitral de Hans Holbein el Joven. Los Hechos de Andrés (Acta Andreae) son un texto cristiano en griego compuesto entre los años 150 y 200, que narra los hechos y la predicación de Andrés el Apóstol. El texto es uno de los Hechos Apócrifos, llamados también Hechos Leucianos porque se consideran que los escribió un presbítero de Asia llamado Leucio Carino (según Focio), aunque existen dudas de que fueran obra únicamente de este autor. El orden relativo de su ...

1910–1961 Dominion of the British Empire For the steam locomotive, see LNER Class A4 4488 Union of South Africa. Union of South AfricaUnie van Zuid-Afrika (Dutch)Unie van Suid-Afrika (Afrikaans)1910–1961 Flag (from 1928) Coat of arms Motto: Ex Unitate Vires (Latin)(From Unity, Strength)Anthem: God Save the King (1910–52); God Save the Queen (1952–57)[a]Die Stem van Suid-Afrika (1938–61)[1](English: The Call of South Africa)Union of South Afri...

Pairs of molecules with same chemical formula showing different spatial orientations Cis-trans redirects here. For other uses, see cis (disambiguation) and trans (disambiguation). cis-but-2-ene trans-but-2-ene Cis–trans isomerism, also known as geometric isomerism, describes a certain arrangement of atoms within molecules. The prefixes cis and trans are from Latin: this side of and the other side of, respectively.[1] In the context of chemistry, cis indicates that the functional gro...

For the AFI song The Checkered Demon, see Answer That and Stay Fashionable. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Checkered Demon – news · newspapers · books · scholar · JSTOR (March 2009) (Learn how and when to remove this template message) Comics character The Checkered DemonThe Checkered Dem...

Style of hair, usually on the human scalp Haircut redirects here. For other uses, see Haircut (disambiguation). Hairdo redirects here. For the Little Birdy song, see Hairdo (song). Hairstyles redirects here. For the magazine, see Hairstyles (magazine). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Hairstyle – news · newspap...

Orde Serafim KerajaanKungliga SerafimerordenBintang ordeDianugerahkan oleh Raja SwediaTipeOrde jasa dengan satu tingkatanNegara SwediaMottoIesus Hominum Salvator (IHS)KelayakanKepala negara lain atau yang setara dan anggota Keluarga Kerajaan Swedia.Dianugerahkan kepadajasa kepada SwediaStatusKini dianugerahkanPenguasaRaja Carl XVI GustafKanselirSvante LindqvistTingkatKesatria(umum: RSerafO/LSerafO,Orang Swedia: RoKavKMO/LoKavKMO)StatistikPenganugerahan pertama1748, Frederick I dari Swedi...

Business which sells, buys, and trades new and/or used cars, trucks, SUVs, and vans The examples and perspective in this article may not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (April 2020) (Learn how and when to remove this template message) Typical car dealership (in this case a Jeep dealer) in the U.S. selling used cars outside, new cars in the showroom, as well as a vehicle entran...

For other uses, see Borana (disambiguation). Zone in Oromia Region of Ethiopia A map of the regions and zones of Ethiopia Borena (Oromo: Boorana) is a zone in Oromia Region of Ethiopia. Borena is named after one of the two major subgroups of the Oromo People. Borena is bordered on the south by Kenya, on the west by the Southern Nations, Nationalities, and Peoples Region, on the north by West Guji and Guji and on the east by Dawa Zone Somali Region. The highest point in this zone is Mount Dara...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (May 2016) (Learn how and when to remove this template message) 2000 studio album by Brian EnoMusic for Civic Recovery CentreStudio album by Brian EnoReleased2000Recorded2000GenreAmbient, dark ambientLength44:50LabelOpalProducerBrian EnoBrian Eno chronology Music for Onmyo-Ji(2000) Music for Civic Recover...

Questa voce contiene un ampio elenco di re e imperatori importanti legati al corso della storia cinese. Indice 1 Premessa 1.1 Scientificità della cronologia 2 Storia 2.1 I re 2.2 Gli imperatori 3 Criteri di compilazione delle tabelle 4 Periodo dei Tre sovrani e dei Cinque Imperatori 5 Dinastia Xia 6 Dinastia Shang 7 Dinastia Zhou 8 Dinastia Qin 9 Dinastia Han 10 Periodo dei Tre Regni 11 Dinastia Jin 12 Periodo dei Sedici Regni 12.1 Sovranità istituite da Wu Hu 13 Dinastie del Nord e del Sud...

Malaysian politician This article is about the Malaysian politician. For the 1955 riot in Montreal, see Richard Riot. Yang Berhormat Dato' SriRichard Riot JaemPJN PNBS SSAP KMN MPSpecial Envoy of the Prime Minister to East AsiaIncumbentAssumed office 15 May 2020MonarchAbdullahPrime MinisterMuhyiddin Yassin (2020–2021) Ismail Sabri Yaakob (2021–2022) Anwar Ibrahim (since 2022)Preceded byTiong King SingConstituencySerianMinister of Human ResourcesIn office16 May 2013 – 10 May...

محافظة سان خوان محافظة سان خوان (جمهورية الدومينيكان) خريطة الموقع تاريخ التأسيس 1938 تقسيم إداري البلد جمهورية الدومينيكان [1][2] العاصمة سان خوان دي لا ماغوانا التقسيم الأعلى جمهورية الدومينيكان خصائص جغرافية إحداثيات 18°49′N 71°14′W / 18.81�...

Tần Nhị Thế秦二世Hoàng đế Trung Hoa (chi tiết...)Nhị Thế lăng (二世陵)Hoàng đế Đại TầnTrị vì210 TCN - 207 TCNTiền nhiệmTần Thủy HoàngKế nhiệmTần Tử AnhThông tin chungSinh230 TCNMất207 TCNTrung QuốcAn tángTần Nhị Thế Lăng (秦二世陵)Tên thậtDoanh Hồ Hợi (嬴胡亥)Tước hiệuNhị Thế Hoàng đế (二世皇帝)Triều đạiNhà TầnThân phụTần Thủy HoàngThân mẫuHồ phu nhân (胡夫人) Tần Nhị T...
