(38779) 2000 RH22
| |||||||||||||||||||||||||||||||||||||||
Read other articles:

Jurina MatsuiJurina Matsui pada tahun 2014Informasi latar belakangNama lahirJurina MatsuiNama lainJurina (じゅりなcode: ja is deprecated )Lahir8 Maret 1997 (umur 27)AsalPrefektur Aichi, Jepang.GenrePopPekerjaan Penyanyi Pemeran Tahun aktif2008 - 2021Artis terkait SKE48 AKB48 Jurina Matsui (松井 珠理奈code: ja is deprecated , Matsui Jurina, lahir 8 Maret 1997) adalah idola Jepang anggota idola Tim S SKE48. Sebagai anggota SKE48, ia secara berturut-turut diikutsertakan sebag...

لمعانٍ أخرى، طالع بروستر (توضيح). بروستر الإحداثيات 41°23′46″N 73°36′57″W / 41.3961°N 73.6158°W / 41.3961; -73.6158 [1] تقسيم إداري البلد الولايات المتحدة[2][3] التقسيم الأعلى مقاطعة بوتنام خصائص جغرافية المساحة 1.280169 كيلومتر مربع1.221069 كيلوم�...

U.S. professional association for healthcare administrators AbbreviationAAPCFormation1988 (1988)FocusHealthcare administrator training and certificationHeadquartersSalt Lake City, Utah Region served United StatesServicesCertification,[1] training,[2] conferences[3]Membership 200,000 (2022)Official language EnglishChief executive officerBevan EricksonWebsitewww.aapc.comFormerly calledAmerican Academy of Professional Coders The AAPC, previously known by the full tit...

Forged documents in the Iraq disarmament crisis This article lists events whose chronological order is ambiguous, backward, or otherwise incorrect. Relevant discussion may be found on the talk page. Please do not remove this message until the described events are arranged in an unambiguous forward-chronological sequence. (February 2024) Wikisource has original text related to this article: Portal:Niger documents Location of Niger in Africa The Niger uranium forgeries were forged documents ini...

Species of bat Pygmy long-eared bat Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Chiroptera Family: Vespertilionidae Genus: Nyctophilus Species: N. walkeri Binomial name Nyctophilus walkeriThomas, 1892[2] The pygmy long-eared bat (Nyctophilus walkeri) is a vesper bat, found in the north of the Australian continent. An insectivorous flying hunter, they are one of ...

Artikel ini bukan mengenai Merdeka (surat kabar). Merdeka.comURLMerdeka.comTipeBeritaPerdagangan ?TidakLangueIndonesiaPemilikSurya Citra Media (KapanLagi Youniverse)PembuatSteve ChristianNegaraIndonesia Peringkat Alexa20 (hingga Februari 2014[update])[1]KeadaanAktif Merdeka.com merupakan sebuah situs berita dari KapanLagi.com yang menyajikan informasi berita Indonesia. Merdeka.com didirikan oleh Steve Christian pada tahun 2011 dengan investasi oleh Sugiono Wiyono dar...

American Roman Catholic priest and bishop Philip Joseph FurlongAuxiliary Bishop of the United States Military VicariateIn office1956-1971OrdersOrdinationMay 18, 1918Personal detailsBorn(1892-09-08)September 8, 1892New York CityDiedApril 13, 1989(1989-04-13) (aged 96)Rectory of St. Thomas MoreDenominationRoman CatholicEducationSt. Joseph's SeminaryAlma materFordham University Philip J. Furlong (September 8, 1892 – April 13, 1989) was a Catholic bishop, serving as Auxiliary Bishop of the...

Tropical cyclone in the North Indian Ocean 1864 Calcutta cycloneFormed2 October 1864Dissipated7 October 1864 Fatalities60,000+Areas affectedIndiaPart of the 1864 North Indian Ocean cyclone season On 5 October 1864, most of the areas of Calcutta (present-day Kolkata), India was inundated and destroyed by a tropical cyclone. Dubbed the 1864 Calcutta cyclone, the storm caused over 60,000 fatalities in its wake. The cyclone crossed the coast of West Bengal to the south of Hooghly River, one of t...

توني ألكساندر آدمز (بالإنجليزية: Tony Adams) معلومات شخصية الميلاد 10 أكتوبر 1966 (العمر 57 سنة)لندن الطول 6 قدم 3 بوصة (1.91 م) مركز اللعب مدافع الجنسية المملكة المتحدة المدرسة الأم جامعة برونيل الرقم 6 مسيرة الشباب سنوات فريق 1980–1983 أرسنال المسيرة الاحترافية1 سن...

Radio station in Walsenburg–Pueblo, Colorado For the economic planning office in South Korea, see Korea Free Economic Zone. KFEZWalsenburg, ColoradoBroadcast areaPueblo, ColoradoWalsenburg, ColoradoRocky Ford, ColoradoColorado Springs, ColoradoFrequency101.3 MHzBrandingGnarly 101.3ProgrammingFormat80's hitsOwnershipOwnerEdward MagnusHistoryFirst air date2009 (as KOCK)Former call signsKWCS (2005–2008)KOCK (2008–2012)Call sign meaningK F EZ (Easy) (previous format)Technical informationFac...

密西西比州 哥伦布城市綽號:Possum Town哥伦布位于密西西比州的位置坐标:33°30′06″N 88°24′54″W / 33.501666666667°N 88.415°W / 33.501666666667; -88.415国家 美國州密西西比州县朗兹县始建于1821年政府 • 市长罗伯特·史密斯 (民主党)面积 • 总计22.3 平方英里(57.8 平方公里) • 陸地21.4 平方英里(55.5 平方公里) • ...

Government building in Zimbabwe Parliament House, HarareFormer Parliament Building of ZimbabweGeneral informationAddressNelson Mandela Avenue (formerly Baker Avenue)Town or cityHarareCountryZimbabweCoordinates17°49′41.4″S 31°03′08.0″E / 17.828167°S 31.052222°E / -17.828167; 31.052222Year(s) built1895-1898Inaugurated31 May 1899Closed7 November 2023OwnerGovernment of ZimbabweWebsiteparlzim.gov.zw Parliament House in Harare was an active legislative building f...

Merry-Joseph BlondelBlondel oleh sahabatnya Ingres, Roma, 1809LahirMerry-Joseph Blondel(1781-07-25)25 Juli 1781Paris, Kerajaan PrancisMeninggal12 Juni 1853(1853-06-12) (umur 71)Paris, Kekaisaran Kedua PrancisKebangsaanPrancisDikenal atasMelukisGerakan politikNeoklasikisme Merry-Joseph Blondel (pengucapan bahasa Prancis: [mɛʁi ʒɔzɛf blɔ̃dɛl]; 25 Juli 1781 – 12 Juni 1853) adalah seorang pelukis sejarah Prancis dari sekolah Neoklasikisme. Dia adalah pemenang dari Prix de Rom...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may need to be rewritten to comply with Wikipedia's quality standards. You can help. The talk page may contain suggestions. (November 2017) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources...

هذه المقالة عن عملية (تحويل فورييه) الرياضية. للفيلسوف الفرنسي، طالع شارل فورييه. تحويل فورييهمعلومات عامةفرع من تحويل تكاملي الاختصار FT سمّي باسم جوزيف فورييه وصفه ISO 80000-2:2019 Quantities and units — Part 2: Mathematics (en) جانب من تحليل فورييه الصيغة ( F f ) ( ω ) = ∫ − ∞ ∞ e "...

Football match1935 FA Cup finalEvent1934–35 FA Cup SheffieldWednesday West BromwichAlbion 4 2 Date27 April 1935VenueWembley Stadium, LondonRefereeBert FoggAttendance93,204← 1934 1936 → The 1935 FA Cup final was contested by Sheffield Wednesday and West Bromwich Albion at Wembley. Sheffield Wednesday won 4–2, with goals scored by Jack Palethorpe, Mark Hooper and Ellis Rimmer (2). Wally Boyes and Teddy Sandford scored West Brom's goals. It is the most recent time that the troph...

2008 film by Anna Chi Dim Sum FuneralDirected byAnna ChiWritten byDonald MartinProduced byClark PetersonStarringBai LingSteph SongTalia ShireJulia NicksonLisa LuKelly HuRussell WongMusic byScott StarrettRelease date November 2008 (2008-11) AFI FestRunning time95 minutesLanguagesEnglish, Mandarin Dim Sum Funeral is a 2008 comedy/drama film directed by Anna Chi and starring Kelly Hu, Bai Ling, Russell Wong, Steph Song and Talia Shire.[1] Premise After their mother dies, four C...
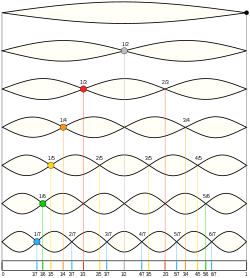
Wave with frequency an integer multiple of the fundamental frequency This article is about the components of periodic signals. For other uses, see Harmonic (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Harmonic – news · newspapers · books · scholar · JSTOR (August 2020) (Learn how and whe...

Political ideologies based on Transhumanism Some of this article's listed sources may not be reliable. Please help improve this article by looking for better, more reliable sources. Unreliable citations may be challenged and removed. (January 2016) (Learn how and when to remove this message) Transhumanism Issues Accelerating change Eradication of suffering Fourth Industrial Revolution Human enhancement Genetic Moral Neuro-) Cognitive liberty New eugenics Eugenics Human nature Meliorism Post-p...

Гиперболический треугольник на седловидной поверхности Гиперболический треугольник — треугольником на гиперболической плоскости. Он состоит из трёх отрезков, называемых сторонами или рёбрами, и трёх точек, называемых углами или вершинами. Как и в евклидовом случае, т�...
