Кубічні сплайни Ерміта
| |||||||||||||||||||||||||||||||||||||||
Read other articles:

Dalam nama Korean ini, nama keluarganya adalah Jo. Jo Yu-riJo, 2021Lahir22 Oktober 2001 (umur 22)Busan, Korea SelatanPekerjaanPenyanyiaktrisKarier musikGenreK-popInstrumenVokalTahun aktif2018–sekarangLabel Stone Music Wake One Off the Record EMI Situs web Situs web resmi Nama KoreaHangul조유리 Hanja曺柔理 Alih AksaraJo Yu-riMcCune–ReischauerCho Yuri Tanda tangan Jo Yu-ri (Hangul: 조유리; lahir 22 Oktober 2001) adalah seorang penyanyi dan aktris asal Korea Selatan. D...

Halaman ini memuat daftar kepala pemerintahan Dominika. Perdana Menteri Dominika adalah kepala pemerintahan di bawah sistem yang diterapkan oleh Konstitusi 1978, beberapa tahun setelah kemerdekaan Dominika. Daftar Kepala Pemerintahan Dominika (1957-Sekarang) # Pejabat Potret Periode Jabatan Afiliasi Politik Awal Jabatan Akhir Jabatan Pemimpin Pemerintahan Dominika (1957-1960) 1 Frank Baron 1957 1 Januari 1960 Partai Rakyat Serikat Dominika Kepala Menteri Dominika (1960-1967) 1 Frank Baron 1 J...

Ilmu-ilmu alam mengalami berbagai kemajuan pada masa Zaman Kejayaan Islam.[1] Selama periode ini, teologi Islam mendorong para pemikir untuk mencari ilmu pengetahuan.[2] para pemikir dari periode ini termasuk Al-Farabi, Abu Bishr Matta, Ibnu Sina, al-Hassan Ibnu al-Haitham, dan Ibnu Bajjah.[3] Studi akademis Islam dalam ilmu pengetahuan telah mewarisi . Penggunaan pengamatan empiris membawa kepada pembentukan bentuk sederhana dari metode ilmiah.[4] Studi fisika...

Bandar Udara Kagoshima鹿児島空港Kagoshima KūkōIATA: KOJICAO: RJFKInformasiJenisPublikPengelolaKementerian Lahan, Infrastruktur, Transportasi dan Pariwisata (lapangan terbang)Kagoshima Airport Building Co., Ltd. (terminal)MelayaniKagoshima, JepangLokasiKirishimaKetinggian dpl mdplPetaKOJLokasi di JepangLandasan pacu Arah Panjang Permukaan m kaki 16/34 3,000 10 Aspal/Beton Source: Japanese AIP at AIS Japan[1] Apron Bandar Udara Kagoshima (鹿児島空港code: ja is depr...

Mario MusolesiSoprannomeLupo NascitaVado di Monzuno, 1º agosto 1914 MorteMarzabotto, 29 settembre 1944 (30 anni) Cause della morteFerite riportate in combattimento Luogo di sepolturaSacrario dei Caduti di Marzabotto Dati militariPaese servito Regno d'Italia Forza armataRegio EsercitoResistenza partigiana ArmaFanteria SpecialitàCarrista Anni di servizio1935-361940-44 GuerreGuerra di EtiopiaSeconda guerra mondiale CampagneCampagna d'Italia (1943-1945) BattaglieLinea Gotica Comand...

Mobil balap milik Leslie Johnson. English Racing Automobiles (ERA) adalah produsen mobil balap Inggris yang aktif dari tahun 1933-1954. Saat ini merek dagang ERA dimiliki oleh produsen kit mobil Inggris. Pabrikan ini sempat turun di ajang Formula Satu dari tahun 1950-1952 dengan beberape pembalap yaitu Leslie Johnson, Peter Walker, Tony Rolt, Cuth Harrison, Bob Gerard, Brian Shawe Taylor, dan yang paling terkenal: Stirling Moss. Pranala luar Wikimedia Commons memiliki media mengenai ERA racin...

Number system extending the rational numbers In this article, unless otherwise stated, p denotes a prime number that is fixed once for all. The 3-adic integers, with selected corresponding characters on their Pontryagin dual group In number theory, given a prime number p, the p-adic numbers form an extension of the rational numbers which is distinct from the real numbers, though with some similar properties; p-adic numbers can be written in a form similar to (possibly infinite) decimals, but ...

Protein-coding gene in the species Homo sapiens ZNF423Available structuresPDBOrtholog search: PDBe RCSB List of PDB id codes2MDGIdentifiersAliasesZNF423, Ebfaz, JBTS19, NPHP14, OAZ, Roaz, ZFP423, Zfp104, hOAZ, zinc finger protein 423External IDsOMIM: 604557 MGI: 1891217 HomoloGene: 9010 GeneCards: ZNF423 Gene location (Human)Chr.Chromosome 16 (human)[1]Band16q12.1Start49,487,524 bp[1]End49,857,919 bp[1]Gene location (Mouse)Chr.Chromosome 8 (mouse)[2]Band8|...

1998 travel book by Bill Bryson A Walk in the Woods First editionAuthorBill BrysonIllustratorDavid CookCountryUnited StatesLanguageEnglishSubjectAppalachian TrailPublisherDoubledayPublication date5 May 1998Media typeHardcoverPages274 pp (first edition)ISBN0-7679-0251-3OCLC37903447Dewey Decimal917.404/43 21LC ClassF106 .B92 1998 A Walk in the Woods: Rediscovering America on the Appalachian Trail is a 1998 travel book by the writer Bill Bryson, chronicling his attempt to thru-hike the...

التعليم عن بعد (بالإنجليزية: Distance Education) والمعروف أيضا بـ التعلم الإلكتروني (بالإنجليزية: Distance Learning) هو أحد طرق التعليم الحديثة نسبيًا.[1][2][3] ويعتمد مفهومه الأساسي على وجود المتعلم في مكان يختلف عن مصدر التعليم الذي قد يكون الكتاب أو المعلم أو حتى مجموعة الدا�...

Non-romantic love This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (January 2014) (Learn how and when to remove this message) Relationships(Outline) Types Genetic or adoptive Kinship Family Parent father mother Grandparent Sibling Cousin By marriage Spouse Husband Wife Open marriage Polygamy Polyandry Polygyny Group marriage Mixed-orientation Partner(s) Signifi...

Hindustani vocal musician Basavraj Rajguru Pandit Basavraj Rajguru (24 August 1920 – 1991) was a leading Indian classical vocalist in the Kirana gharana (singing style). Early life and training Basavraj was born into a family of scholars, astrologers and musicians in Yaliwal, a village in the north Karnataka district of Dharwad, a great centre of classical music. He was initiated into classical music at an early age by his father, who was himself a renowned Carnatic musician trained in...

The Knack …and How to Get ItPoster bioskopSutradaraRichard LesterProduserOscar LewensteinDitulis olehCharles WoodPemeranRita TushinghamRay BrooksMichael CrawfordDonal DonnellyPenata musikJohn BarrySinematograferDavid WatkinPenyuntingAntony GibbsPerusahaanproduksiWoodfall Film ProductionsDistributorUnited Artists CorporationTanggal rilis3 Juni 1965 (1965-06-03)Durasi85 menitNegaraBritania RayaBahasaInggrisAnggaran$364.000[1][2]Pendapatankotor$2,5 juta (AS)[1 ...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Cet article est une ébauche concernant la Hongrie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Hongrie septentrionale Észak-Magyarország Hongrie septentrionale et ses trois départements Administration Pays Hongrie Centre Miskolc Code Nuts HU31 Démographie Population 1 236 690 hab. Densité 92 hab./km2 Géographie Coordonnées 48° 06′ nord, 20° 46′ est Superf...

Serasah di dasar hutan Serasah atau sarap[butuh rujukan] adalah istilah yang diberikan untuk sampah-sampah organik yang berupa tumpukan dedaunan kering, rerantingan, dan berbagai sisa vegetasi lainnya di atas lantai hutan atau kebun yang sudah mengering dan berubah dari warna aslinya. Serasah kebanyakan memiliki senyawa berbasis karbon. Serasah yang telah membusuk (mengalami dekomposisi) berubah menjadi humus (bunga tanah) dan akhirnya menjadi tanah. Pengomposan serasah memiliki peran...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: KOVC – news · newspapers · books · scholar · JSTOR (January 2013) (Learn how and when to remove this message) Radio station in Valley City, North DakotaKOVCValley City, North DakotaFrequency1490 kHzProgrammingFormatFull service countryAffiliationsFox News RadioMinnesota Timberwo...

Art of the Jewish people Mordecai and Esther, Dura Europos Synagogue, 3rd century Jewish art, or the art of the Jewish people, encompasses a diverse range of creative endeavors, spanning from ancient Jewish art to contemporary Israeli art. Jewish art encompasses the visual plastic arts, sculpture, painting, and more, all influenced by Jewish culture, history, and religious beliefs. Jewish artistic expression traces back to the art of the ancient Israelites in the Land of Israel, where it orig...

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (February 2023) (Learn how and when to remove this message) Events leading to the American Civil War Economic End of Atlantic slave trade Panic of 1857 Political Northwest Ordinance Kentucky and Virginia Resolutions Missouri Compromise Nullification crisis Gag rule Tariff of 182...

Pour les articles homonymes, voir Traille. Damien Traille Damien Traille en 2015. Fiche d'identité Naissance 12 juin 1979 (45 ans)Pau (France) Taille 1,92 m (6′ 4″) Poste Centre, arrière, demi d'ouverture Carrière en junior PériodeÉquipe US Coarraze Nay Carrière en senior PériodeÉquipeM (Pts)a 1998-20042004-20142014-2016 Section paloiseBiarritz olympiqueSection paloise 101 (91)[1]229 (306)[1]33 (29)[1] Carrière en équipe nationale PériodeÉquipeM (Pts)b 20...






















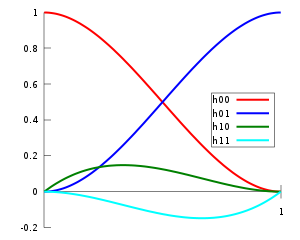
![{\displaystyle \mathbf {p} (t)=h_{00}(t)\mathbf {p_{0}} +h_{10}(t)\mathbf {m_{0}} +h_{01}(t)\mathbf {p_{1}} +h_{11}(t)\mathbf {m_{1}} ,\qquad t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ea37ce43183b72d3917aa76eadf1324d4e10139)















