Лемніската Бернуллі
| |||||||||||||
Read other articles:

Untuk energi terendah dari fungsi gelombang elektron dalam fisika atom, lihat orbital atom. Untuk gelombang S pada elektrokardiogram, lihat kompleks QRS. Gelombang geser bidangPerambatan gelombang-S sferis pada kisi 2 dimensi (model empiris) Dalam seismologi dan bidang lainnya yang melibatkan gelombang elastis, gelombang-S, gelombang sekunder, atau gelombang geser (terkadang disebut sebagai gelombang-S elastis) adalah suatu jenis gelombang elastis dan merupakan salah satu dari dua jenis gelom...

International standard for spacecraft docking adapters IDSS Rev D NDS, NASA's implementation of IDSS The International Docking System Standard (IDSS) is an international standard for spacecraft docking adapters. It was created by the International Space Station Multilateral Coordination Board, on behalf of the International Space Station partner organizations; NASA, Roscosmos, JAXA, ESA, and the Canadian Space Agency. The IDSS was originally formulated in 2010.[1] The plan is for all ...

Val CamonicaMonte Concarena, media Val CamonicaStati Italia Regioni Lombardia Province Brescia Bergamo Località principaliAngolo Terme, Artogne, Berzo Demo, Berzo Inferiore, Bienno, Borno, Braone, Breno, Capo di Ponte, Castro, Cedegolo, Cerveno, Ceto, Cevo, Cimbergo, Cividate Camuno, Corteno Golgi, Darfo Boario Terme, Edolo, Esine, Gianico, Incudine, Losine, Lovere, Lozio, Malegno, Malonno, Monno, Niardo, Ono San Pietro, Ossimo, Paisco Loveno, Paspardo, Pian Camuno, Pianc...

Holding company of several car rental brands For the Houston-based energy company, see Enterprise Products. Enterprise Holdings, Inc.Company typePrivateIndustryTravelFounded1957; 67 years ago (1957)August 3, 2009; 14 years ago (2009-08-03) (as holding company)FounderJack C. TaylorHeadquartersClayton, Missouri, United StatesNumber of locations9,500 branches (2020)Key peopleAndrew C. Taylor (executive chairman)Chrissy Taylor (president & CEO)BrandsAl...

Mappa delle contee del Texas con la densità di popolazione. Lo Stato del Texas è diviso in 254 contee. È lo Stato con il maggior numero di contee degli USA.[1] In origine il Texas era diviso in comuni, una unità di governo locale vigente sotto il dominio spagnolo e messicano. Quando la Repubblica del Texas ottenne l'indipendenza nel 1836, esistevano ventitré comuni, che divennero le contee originarie del Texas. Molte di queste si sarebbero in seguito divise in nuove contee. La co...

Voce principale: Associazione Calcio Legnano. A.C. LegnanoStagione 1971-1972I Lilla con la seconda maglia bianca con banda Sport calcio Squadra Legnano Allenatore Luciano Sassi Presidente Augusto Terreni Serie C9º posto nel girone A Maggiori presenzeCampionato: Mongitore (38) Miglior marcatoreCampionato: Bosani (11) StadioComunale 1970-1971 1972-1973 Si invita a seguire il modello di voce Questa pagina raccoglie le informazioni riguardanti l'Associazione Calcio Legnano nelle compet...

Anita EkbergEkberg pada 1956PelafalanSwedia: [a²niːta ²eːkbærj] simakⓘ Italia: [aˈniːta ˈɛkberɡ] bahasa Inggris: /əˈniːtə ˈɛkbɜːrɡ/LahirKerstin Anita Marianne Ekberg(1931-09-29)29 September 1931Malmö, SwediaMeninggal11 Januari 2015(2015-01-11) (umur 83)Rocca di Papa, ItaliaKebangsaanSwediaPekerjaanPemeran, peraga busanaTahun aktif1953–2002Suami/istriAnthony Steel (m. 1956–1959) Rik Van Nu...

Slocomb, AlabamaKotaNegara Amerika SerikatNegara bagianlbs Negara bagian AlabamaMontgomery (ibu kota)Topik Sejarah Geografi Orang Pemerintah Gubernur Wakil gubernur Kawasan Metropolitan Tempat wisata Landmark Nasional Bersejarah Wilayah Atlantic Coastal Plain Birmingham District Black Belt Central Alabama Cumberland Plateau Greater Birmingham Gulf Coastal Plain Lower Alabama Mobile Bay North Alabama Northeast Alabama Northwest Alabama Piedmont Ridge and Valley River Region South Ala...

American neo-Nazi cartoonist Stonetoss redirects here. For other uses, see Stone tossing. StoneTossNationalityAmericanArea(s)CartoonistPseudonym(s)StoneTossNotable worksStoneTossCurrent status/scheduleOngoingLaunch dateJuly 18, 2017[1]Publisher(s)Self-published (webcomic)Genre(s)Far-right political cartoon[2]Original languageEnglish stonetoss.com Part of a series onAntisemitism Part of Jewish history and discrimination History Timeline Reference Definitions IHRA definition of ...

Manor house in Surrey, EnglandLoseley ParkTypeManor houseLocationLittleton Lane, Artington, Surrey, EnglandCoordinates51°12′55″N 0°36′18″W / 51.2152°N 0.6049°W / 51.2152; -0.6049OS grid referenceSU 97495 47149Built1568Architectural style(s)TudorOwnerMore-Molyneux family[1] Listed Building – Grade IOfficial nameLoseley HouseDesignated18 February 1958Reference no.1029573 Location of Loseley Park in Surrey Loseley Park is a large Tudor manor ho...

Species of bird Thick-billed raven In Ethiopia Conservation status Least Concern (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Passeriformes Family: Corvidae Genus: Corvus Species: C. crassirostris Binomial name Corvus crassirostrisRüppell, 1836 The thick-billed raven (Corvus crassirostris), a corvid from the Horn of Africa, shares with the common raven the distinction of being the largest bird in the corvid...

The Man Who Saw TomorrowIklan surat kabarSutradaraAlfred E. GreenProduserAdolph ZukorSkenarioFrank CondonWill M. RitcheyPerley Poore SheehanPemeranThomas MeighanTheodore RobertsLeatrice JoyAlan RoscoeAlec B. FrancisJune ElvidgeEva NovakSinematograferAlvin WyckoffPerusahaanproduksiFamous Players-Lasky CorporationDistributorParamount PicturesTanggal rilis 29 Oktober 1922 (1922-10-29) Durasi70 menitNegaraAmerika SerikatBahasaBisu (intertitel Inggris) The Man Who Saw Tomorrow adalah sebuah f...

Abjad Aram atau Abjad Aramaik adalah aksara yang dipakai dalam Bahasa Aram, oleh masyarakat Aram, yang tinggal di daerah sekitar Siria sekarang dan Mesopotamia. Aksara ini digunakan sekitar abad ke-10 SM. Dari aksara ini menurunkan aksara Arab dan aksara Brahmi. Aksara ini memiliki sifat alfabetis dan terdiri dari 22 konsonan.[1] Abokeunn Tabel abjad dan perbandingan dengan abjad turunan atau sejenis Nama huruf Tulisan Aram Tulisan Siria Huruf Huruf sejenis dalam IPA Ibrani Arab Brahm...

DFB Pokal 1990/91 Competizione Coppa di Germania Sport Calcio Edizione 48ª Date 3 agosto 1990 - 22 giugno 1991 Luogo Germania Ovest - Germania Partecipanti 64 Risultati Vincitore Werder Brema(2º titolo) Secondo Colonia Statistiche Miglior marcatore Michael Tönnies (6) Incontri disputati 69 Gol segnati 228 (3,3 per incontro) Cronologia della competizione 1989-1990 1991-1992 Manuale La DFB-Pokal 1990–91 fu la 48ª edizione del torneo che si svolse tra il 3 agos...
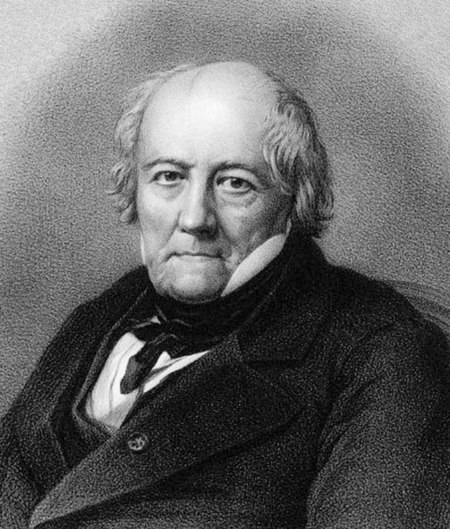
French physicist Jean-Baptiste BiotJean-Baptiste BiotBorn21 April 1774 (1774-04-21)Paris, FranceDied3 February 1862(1862-02-03) (aged 87)Paris, FranceNationalityFrenchAlma materÉcole PolytechniqueKnown forBiot numberBiot–Savart lawCircular dichroismOptical rotationAwardsPour le Mérite (1850)Rumford Medal (1840)ForMemRS (1815)Scientific careerFieldsPhysics, astronomy and mathematicsAcademic advisorsGaspard Monge[1] Signature Jean-Baptiste Biot (/ˈbiːoʊ, ˈbjo...

この項目「石油輸出国機構」は加筆依頼に出されており、内容をより充実させるために次の点に関する加筆が求められています。加筆の要点 - 統計の更新・エクアドルの脱退(貼付後はWikipedia:加筆依頼のページに依頼内容を記述してください。記述が無いとタグは除去されます)(2020年6月) 石油輸出国機構Organization of the Petroleum Exporting Countries(OPEC) OPECの旗設立 1960年9�...

殺人行おくのほそ道 小説冒頭で言及され『おくのほそ道』ゆかりの土地の一つとなる鳴子温泉作者 松本清張国 日本言語 日本語ジャンル 長編小説発表形態 雑誌連載初出情報初出 『ヤングレディ』 1964年7月6日 - 1965年8月23日初出時の題名 『風炎』出版元 講談社挿絵 田代光刊本情報刊行 『殺人行おくのほそ道』上下巻出版元 講談社出版年月日 1982年5月20日装幀 市川英夫...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (أغسطس 2019) هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسي...

Ben & Tan Ben & Tan lors du Dansk Melodi Grand Prix 2020Informations générales Pays d'origine Danemark Genre musical Pop Années actives Depuis 2020 Composition du groupe Membres Benjamin RosenbohmTanne Balcells modifier Ben & Tan est un duo danois composé de Benjamin Rosenbohm (né le 3 juin 2002) et Tanne Balcells (née le 15 janvier 1998). Ils devaient représenter le Danemark au Concours Eurovision de la chanson 2020 à Rotterdam, avec la chanson Yes, jusqu'à ce qu'il soi...

Scuola Antonio BenciVeduta del prospetto principaleLocalizzazioneStato Italia RegioneToscana LocalitàLivorno Indirizzoscali degli Olandesi Coordinate43°32′57.54″N 10°18′47.95″E43°32′57.54″N, 10°18′47.95″E Informazioni generaliCondizioniIn uso Costruzionefine XIX secolo Inaugurazione1893 Stilearchitettura eclettica Usoscuola RealizzazioneArchitettoAngiolo Badaloni ProprietarioComune di Livorno Modifica dati su Wikidata · Manuale La Scuola Antonio Benci è una st...






























![{\displaystyle \varphi \in \left[0,{\frac {\pi }{4}}\right]\cup \left[{\frac {3\pi }{4}},{\frac {5\pi }{4}}\right]\cup \left[{\frac {7\pi }{4}},2\pi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11be43317f89581ff6fe634be3e11b48e7ffc444)
![{\displaystyle \varphi \in \left[-{\frac {\pi }{4}},{\frac {\pi }{4}}\right]\cup \left[{\frac {3\pi }{4}},{\frac {5\pi }{4}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b3f461a5b8bb336e9bbf64e2c0412f86fcc917b)























































![{\displaystyle \varphi \in [0,\varphi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b27d2a332b2a150fbbc74fabe56616527446d32)




































