П'ята проблема Гільберта
|
Read other articles:

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

The RiverSutradaraPare LorentzDitulis olehPare LorentzSinematograferFloyd CrosbyWillard Van DykeStacy WoodardDistributorFarm Security AdministrationTanggal rilis4 Februari 1938 (1938-02-04)Durasi31 menitNegaraAmerika SerikatBahasaInggris The River adalah sebuah film dokumenter pendek 1938 yang menampilkan pengaruh Sungai Mississippi bagi Amerika Serikat, dan kenapa praktik penebangan dan perkebunan telah menyebabkan pengikisan tanah di pinggiran sungai dan Teluk Meksiko, berujung pada ba...

Italian footballer and manager Lido Vieri Vieri c. 1970Personal informationFull name Lido VieriDate of birth (1939-07-16) 16 July 1939 (age 84)Place of birth Piombino, ItalyHeight 1.83 m (6 ft 0 in)Position(s) GoalkeeperYouth career1954–1957 TorinoSenior career*Years Team Apps (Gls)1957–1969 Torino 275 (0)1957–1958 → Vigevano (loan) 31 (0)1969–1976 Inter Milan 140 (0)1976–1980 Pistoiese 63 (0)Total 499 (0)International career1963–1968 Italy 4 (0)Managerial ca...
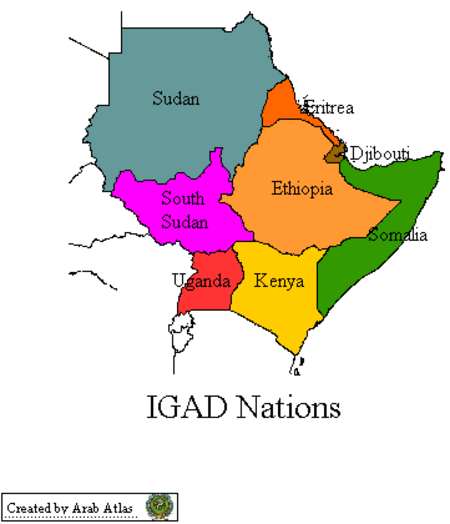
Autorità intergovernativa per lo sviluppo(EN) Intergovernmental Authority on Development Paesi appartenenti all'IGAD AbbreviazioneIGAD Tipounione doganale sovranazionale Affiliazione internazionaleUnione Africana Fondazionegennaio 1986 Sede centrale Gibuti Area di azioneCorno d'Africa Lingue ufficialiarabo, swahili Membri7 stati Sito web Modifica dati su Wikidata · Manuale L'Autorità intergovernativa per lo sviluppo (in inglese Intergovernamental Authority on Development - IGA...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (janvier 2017). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique : Quelles sources sont attendues ? C...

Red Bull RB4 Mark Webber guida la RB4 in un test Descrizione generale Costruttore Red Bull Racing Categoria Formula 1 Squadra Red Bull Racing Progettata da Adrian NeweyGeoff WillisRob MarshallPeter Prodromou Sostituisce Red Bull RB3 Sostituita da Red Bull RB5 Descrizione tecnica Meccanica Telaio Monoscocca composita in fibra di carbonio Motore Renault RS27-2008 2.4 V8 Trasmissione Longitudinale in alluminio 7 rapporti + retro Dimensioni e pesi Peso 605 kg Altro Carburante Elf Pneumatic...

Relief Gandaberunda di Istana Mysuru. Gandaberunda (Dewanagari: गण्डभेरुण्ड; ,IAST: Gaṇḍabheruṇḍa,; arti: berleher hebat) atau Berunda (Dewanagari: भेरुण्ड; ,IAST: Bheruṇḍa,; arti: dahsyat) adalah burung berleher dua dalam mitologi Hindu, yang merupakan salah satu penjelmaan Wisnu. Menurut mitologi Hindu, ia memiliki kekuatan gaib yang sangat besar.[1] Menurut aliran Waisnawa, ia dihormati sebagai salah satu...

Governing body of association football in Turkey Turkish Football FederationUEFAShort nameTFFFounded23 April 1923; 101 years ago (1923-04-23)HeadquartersIstanbulFIFA affiliation1923UEFA affiliation1962PresidentMehmet BüyükekşiWebsitewww.tff.org Turkish Football Federation Facility at Riva, Beykoz in Istanbul The Turkish Football Federation (Turkish: Türkiye Futbol Federasyonu; TFF) is the governing body of association football in Turkey. It was formed on 23 April 1923, a...

Міністерство оборони України (Міноборони) Емблема Міністерства оборони та Прапор Міністерства оборони Будівля Міністерства оборони у КиєвіЗагальна інформаціяКраїна УкраїнаДата створення 24 серпня 1991Попередні відомства Міністерство оборони СРСР Народний комісарі...

1967 novel by Robert Lipsyte This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Contender Lipsyte novel – news · newspapers · books · scholar · JSTOR (November 2021) (Learn how and when to remove this message) The Contender First editionAuthorRobert LipsyteCover artistRobert LipsyteCountryUnited StatesLanguageEngli...

Filattiera komune di Italia Tempat Negara berdaulatItaliaDaerah di ItaliaToscanaProvinsi di ItaliaProvinsi Massa-Carrara NegaraItalia Ibu kotaFilattiera PendudukTotal2.185 (2023 )GeografiLuas wilayah48,78 km² [convert: unit tak dikenal]Ketinggian213 m Berbatasan denganCorniglio Pontremoli Villafranca in Lunigiana Bagnone Mulazzo SejarahSanto pelindungStefanus Informasi tambahanKode pos54023 Zona waktuUTC+1 UTC+2 Kode telepon0187 ID ISTAT045006 Kode kadaster ItaliaD590 Lain-lainSit...

Saudi Arabian state-owned petroleum company Saudi Arabian Oil GroupHeadquarters in Dhahran, Eastern Province, Saudi ArabiaTrade nameSaudi AramcoNative nameشركة الزيت العربية السعوديةCompany typePublic (mostly state-owned)Traded asTadawul: 2222ISINSA14TG012N13 IndustryOil and gasFounded29 May 1933; 91 years ago (29 May 1933) (as California-Arabian Standard Oil)FounderStandard Oil of California (at the behest of the Saudi government)HeadquartersDha...

NOAA environmental products and services Oceanic and Atmospheric ResearchNational Oceanic and Atmospheric Administration sealAgency overviewFormed1841; 183 years ago (1841)HeadquartersSilver Spring, Maryland, U.S.[1]MottoOAR's Vision is to deliver NOAA’s future. OAR's Mission is to conduct research to understand and predict the Earth’s oceans, weather and climate, to advance NOAA science, service and stewardship and transition the results so they are useful to so...

Positive integer whose divisors have a harmonic mean that is an integer This article is about harmonic divisor numbers. For meanings of harmonic number, see harmonic number (disambiguation). In mathematics, a harmonic divisor number or Ore number is a positive integer whose divisors have a harmonic mean that is an integer. The first few harmonic divisor numbers are 1, 6, 28, 140, 270, 496, 672, 1638, 2970, 6200, 8128, 8190 (sequence A001599 in the OEIS). Harmonic divisor numbers were introduc...

American Jesuit Catholic magazine America MagazineEditorSam Sawyer, S.J.Former editorsDrew ChristiansenThomas J. ReeseCategoriesChristianity (Catholicism)FrequencyMonthlyCirculation45,000PublisherAmerican JesuitsFounded 1909 (1909-month)CompanyAmerica MediaCountryUnited StatesBased inNew York CityLanguageEnglishWebsitewww.americamagazine.org ISSN0002-7049 America is a monthly Catholic magazine published by the Jesuits of the United States and headquartered in midtown Manhattan. It c...

Badminton tournament in Malaysia Badminton tournament2024 Malaysia OpenTournament detailsDates9–14 JanuaryEdition67thLevelSuper 1000Total prize moneyUS$1,300,000VenueAxiata ArenaLocationKuala Lumpur, MalaysiaChampionsMen's singles Anders AntonsenWomen's singles An Se-youngMen's doubles Liang Weikeng Wang ChangWomen's doubles Liu Shengshu Tan NingMixed doubles Yuta Watanabe Arisa Higashino ← 2023 2025 → The 2024 Malaysia Open (officially known as the Petronas Malaysia Open 2024 for spons...

Soviet medium- to long-range airliner with 4 turboprop engines, 1957 For the 1946 prototype airliner, see Ilyushin Il-18 (1946). For the Soviet jet-engined bomber, see Ilyushin Il-22. Il-18 / Il-20 / Il-22 A Russian Air Transport Il-18 Role Turboprop airliner and reconnaissance aircraftType of aircraft National origin Soviet Union Manufacturer Moscow Machinery Plant No. 30 Designer Ilyushin First flight 4 July 1957 Status In limited service Primary users Aeroflot Soviet Airlines (Histori...

Area of Holyhead, Anglesey, Wales This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Llaingoch – news · newspapers · books · scholar · JSTOR (October 2013) (Learn how and when to remove this message) 53°18′40″N 4°39′58″W / 53.311°N 4.666°W / 53.311; -4.666 Llaingoch (Welsh pronunciationⓘ) is...

Questa voce o sezione sugli argomenti fibre e polimeri non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Sintesi di un poliuretano a partire da un di-isocianato e da un diolo. Nanofibre di poliuretano viste al microscopio. Poliuretano (PU o PUR) indica una vasta famiglia di polimeri in cui la catena polimerica è costituita di legami uretanici, la cui form...

Alan ShearerCBE DL Thông tin cá nhânTên đầy đủ Alan Shearer[1]Chiều cao 1,83 m (6 ft 0 in)Vị trí Tiền đạoSự nghiệp cầu thủ trẻNăm Đội000 Wallsend Boys Club1986–1988 CLB SouthamptonSự nghiệp cầu thủ chuyên nghiệp*Năm Đội ST (BT)1988–1992 CLB Southampton 158 (43)1992–1996 Blackburn Rovers 171 (130)1996–2006 Newcastle United 405 (206)Tổng cộng 733 (379)Sự nghiệp đội tuyển quốc giaNăm Đội ST (BT)199...













