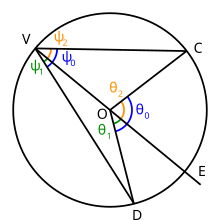
Çevre açı
|
Read other articles:

Secretary general of NATO since 2014 Jens StoltenbergStoltenberg in 202313th Secretary General of NATOIncumbentAssumed office 1 October 2014DeputyAlexander VershbowRose Gottemoeller Mircea GeoanăPreceded byAnders Fogh Rasmussen34th Prime Minister of NorwayIn office17 October 2005 – 16 October 2013MonarchHarald VPreceded byKjell Magne BondevikSucceeded byErna SolbergIn office17 March 2000 – 19 October 2001MonarchHarald VPreceded byKjell Magne BondevikSucceeded by...

Charitable organization Christopher and Dana Reeve FoundationLogo as of September 2008Founded1982LocationShort Hills, New Jersey, U.S.Key peopleJay Shepard(Chairman)Peter T. Wilderotter(President and CEO)Websitewww.christopherreeve.org The Christopher & Dana Reeve Foundation is a charitable organization headquartered in Short Hills, New Jersey, dedicated to finding treatments and cures for paralysis caused by spinal cord injury and other neurological disorders. The organization's mission ...
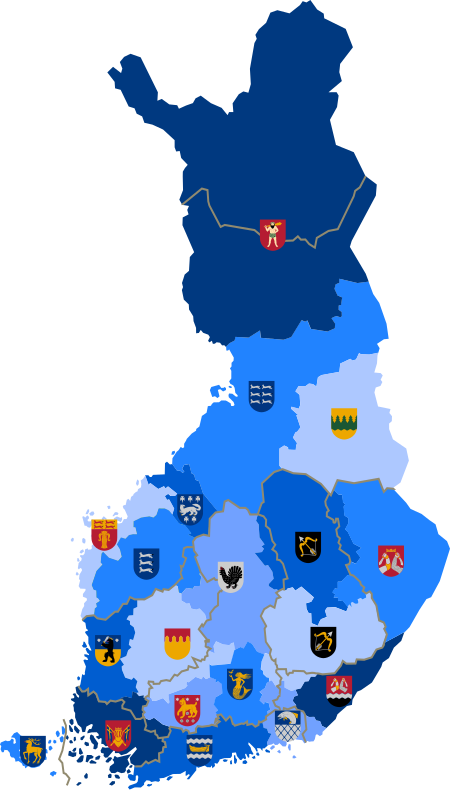
Peta pembagian administratif tingkat pertama Finlandia Pembagian administratif Finlandia terdiri atas 19 region (maakunta) pada tingkat pertama dan 70 subregion (seutukunta) pada tingkat kedua. lbsPembagian administratif EropaNegaraberdaulat Albania Andorra Armenia1 Austria Azerbaijan1 Belanda Belarus Belgia Bosnia dan Herzegovina Britania Raya Inggris Irlandia Utara Skotlandia Wales Bulgaria Ceko Denmark Estonia Finlandia Georgia1 Hungaria Republik Irlandia Islandia Italia Jerman Kazakhstan2...

Taman Kencana (Sunda: ᮒᮙᮔ᮪ ᮊᮔ᮪ᮎᮔ, translit. Taman Kancana) merupakan taman kecil di antara area hijau di Kota Bogor yang semakin lama semakin menghilang seiring dengan kemajuan pembangunan kota. Taman ini merupakan salah satu peninggalan zaman Belanda. Didukung dengan suasana di sekitarnya yang masih rindang dengan pepohonan, taman ini sekaligus menjadi tempat rekreasi dan semacam titik pertemuan bagi sebagian masyarakat Kota Bogor dan berbagai macam komunitas seper...

Перуанский анчоус Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёрые �...

Asian Film AwardsPenghargaan terkini: Penghargaan Film Asia ke-10Rancangan trofi Asian Film Awards yang dibuat oleh William Chang yang digunakan pada Penghargaan Film Asia ke-3 2009DeskripsiKesempurnaan dalam prestasi sinematikLokasiHong Kong, TiongkokNegaraAsiaDipersembahkan olehPersatuan Festival Film Internasionl Hong KongDiberikan perdana2007Situs webwww.asianfilmawards.asia Asian Film Awards adalah sebuah acara penghargaan yang diselenggarakan setiap tahun oleh Persatuan Festival Film In...

American baseball umpire (1930–2018) For the NHL player, see Doug Harvey (ice hockey). Doug HarveyHarvey at the 2011 Baseball Hall of Fame induction paradeBorn(1930-03-13)March 13, 1930South Gate, California, U.S.DiedJanuary 13, 2018(2018-01-13) (aged 87)Visalia, California, U.S.EducationSan Diego State UniversityOccupationBaseball umpireYears active1962–1992Spouses Joan Manning (m. 1950; div. 1952) Joy Glascock (...

У этого термина существуют и другие значения, см. Западный округ. Западный внутригородской округ город Краснодар Дата основания 1936 год Дата упразднения 1994 Прежние имена Кагановичский, Ленинский районы Микрорайоны Дубинка, Черёмушки, Покровка Площадь 22[1] км² Насе...

关于与「友谊勋章 (俄罗斯)」標題相近或相同的条目页,請見「友谊勋章 (消歧义)」。 友谊勋章类型单级勋章(仅设有一个等级)授予原因加强各民族友谊、交流与合作国家/地区俄罗斯 颁发单位 俄羅斯颁授资格俄罗斯国民及世界各民族人民設立時間1994年3月2日[1]首次颁发康斯坦丁·蒂托夫(萨马拉州州长)绶带 优先顺序上等荣誉勋章下等光荣父母�...

Scottish footballer Pauline Hamill Hamill (11) playing against Northern Ireland in May 2009Personal informationDate of birth (1971-12-18) 18 December 1971 (age 52)[1]Place of birth Motherwell, ScotlandPosition(s) Winger, StrikerTeam informationCurrent team Saudi Arabia women's U20 (head coach)Youth career Craigburn Boys Club Coltness LadiesSenior career*Years Team Apps (Gls) Cumbernauld Ladies Stenhousemuir Ladies Kilmarnock Ladies 2001 ÍBV 2002–2005 Hibernian Ladies 2005&...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

Muscatatuck Urban Training CenterJennings County, Indiana Coordinates39°03′05″N 85°32′09″W / 39.0513°N 85.5358°W / 39.0513; -85.5358TypeMilitary Training BaseSite informationControlled byUnited StatesSite historyBuilt1919In use2005-presentGarrison informationGarrisonCurrent Site Manager - LTC John Pitt (2017-Present) Past Commanders - LTC Barry Hon (2013-2016), LTC R. Dale Lyles (2010-2013), LTC Chris Kelsey (2008-2010), LTC Ken McCallister (2005-...

Overview of the geography of Berlin Berlin skyline with Berliner Fernsehturm left and skyscrapers of Potsdamer Platz to the right Location of Berlin in the European Union and Germany Berlin is the capital city of Germany and one of the 16 states of Germany. With a population of 3.4 million people, Berlin is the most populous city proper, the sixth most populous urban area in the European Union, and the largest German city.[1] Located in northeastern Germany on the River Spree, it...

Carpeneto komune di Italia Tempat Negara berdaulatItaliaDaerah di ItaliaPiemonteProvinsi di ItaliaProvinsi Alessandria NegaraItalia Ibu kotaCarpeneto PendudukTotal889 (2023 )GeografiLuas wilayah13,34 km² [convert: unit tak dikenal]Ketinggian329 m Berbatasan denganMontaldo Bormida Ovada Predosa Rocca Grimalda Sezzadio Trisobbio Acqui Terme SejarahHari liburpatronal festival Santo pelindungSanto George Informasi tambahanKode pos15071 Zona waktuUTC+1 UTC+2 Kode telepon0143 ID ISTAT00...

Ancient French word for part of a city Turgot map of Paris (1734–1736), showing part of the Faubourg Saint-Michel and Faubourg Saint-Jacques. Faubourg (French: [fo.buːʁ]) is an ancient French term historically equivalent to fore-town (now often termed suburb or banlieue). The earliest form is forsbourg, derived from Latin forīs, 'out of', and Vulgar Latin (originally Germanic) burgum, 'town' or 'fortress'. Traditionally, this name was given to an agglomeration forming around a th...

Moon of Uranus BelindaBelinda viewed by Voyager 2 in 1986DiscoveryDiscovered byStephen P. Synnott / Voyager 2Discovery dateJanuary 13, 1986DesignationsDesignationUranus XIVPronunciation/bəˈlɪndə/[1]AdjectivesBelindianOrbital characteristics[2]Semi-major axis75 255.613 ± 0.057 kmEccentricity0.00007 ± 0.000073Orbital period (sidereal)0.623527470 ± 0.000000017 dInclination0.03063 ± 0.028° (to Uranus' equator)Satellite ofUranusPhysical characteristicsDimens...

Swimming competition Men's 100 metre butterfly S11at the XVI Paralympic GamesVenueTokyo Aquatics CentreDates3 September 2021Competitors13 from 9 nationsMedalists Keiichi Kimura Japan Uchu Tomita Japan Wendell Belarmino Pereira Brazil Swimming at the2020 Summer ParalympicsMen's events50 m freestyleS3S4S5S7S9S10S11S13100 m freestyleS4S5S6S8S10S12200 m freestyleS2S3S4S5S14400 m freestyleS6S7S8S9S10S11S1350 m backstrokeS1S2S3S4S5100 m backstrokeS1S2S6S7S8S9S10S11S12S13...

For other uses, see Angers (disambiguation). Not to be confused with Algiers. Prefecture and commune in Pays de la Loire, FranceAngersPrefecture and communeTop to bottom, left to right: Château d'Angers, Maison d'Adam; Angers tram, Verdun Bridge at night; view of the river Maine, Verdun Bridge and downtown area from Angers Castle FlagCoat of armsLocation of Angers AngersShow map of FranceAngersShow map of Pays de la LoireCoordinates: 47°28′25″N 0°33′15″W / 47.473612...

Battle of the French and Indian War Battle of Fort FrontenacPart of the Seven Years' WarFrench and Indian WarDepiction of the battle by John Henry WalkerDateAugust 26–28, 1758Locationpresent-day Kingston, Ontario44°14′00″N 76°28′43″W / 44.23333°N 76.47861°W / 44.23333; -76.47861Result British victoryBelligerents Great Britain British America France Colony of CanadaCommanders and leaders John Bradstreet Pierre-Jacques Payen de Noyan et de Chavo...

Tool to clear blockages in drains and pipes This article is about the plumbing tool. For other uses, see Plunger (disambiguation). Plumbing plunger A plunger is a device driven by or against fluid pressure.[1] In plumbing, the term plunger commonly refers to handheld tools used to clear blockages in drains and pipes. Plumbing plungers consist of a rubber suction cup attached to a stick (shaft) usually made of wood or plastic. A different bellows-like design also exists, usually constr...