VektorU elementarnoj matematici i fizici, a napose u tehničkim primjenama, vektor najčešće označava veličinu koja ima iznos i smjer, te zadovoljava pravila vektorskog računa. Taj se opis odnosi na veličine u trodimenzionalnom prostoru iz našeg svakodnevnog iskustva, koji u matematici najbolje opisuje Euklidski prostor. Vektori su uvedeni kao složenije veličine od skalara; skalari su u nevedenom kontekstu veličine koje imaju samo brojčanu vrijednost koja može biti pozitivna, 0 ili negativna, tj. opisuju se jednim realnim brojem. Za opis vektora u trodimenzionalnom prostoru potrebna su tri realna broja - npr. jedan za iznos i dva za smjer (kutovi), ili tri skalarne komponente u koordinatnom sustavu. Još složenije veličine od vektora su tenzori, preciznije tenzori drugoga reda i viših redova, koji se u trodimenzionalnom prostoru opisuju sa 9, 27 ili više brojeva. U tenzorskom opisu, skalari su tenzori nultoga reda, a vektori su tenzori prvoga reda. Formalno i općenito, međutim, pojam vektora se u matematici, pa i fizici, i u drugim primjenama, definira znatno apstraktnije. Pristup se najčešće temelji na definiciji vektorskog prostora iz linearne algebre gdje se koriste višedimenzionalni (pa i beskonačno dimenzionalni) prostori nad poljem realnih ili kompleksnih skalara. Ipak, i u te opće definicije ugrađene su analogije s gore navedenim slučajem iz "običnog" trodimenzionalnog prostora. Veći dio ovoga članka ukratko izlaže jedan od mogućih "matematičkih" opisa u prostoru od n dimenzija, no mnogi su rezulatati izravno primjenjljivi na "obične" trodimenzionalne vektore. Iako je to matematičko izlaganje "mekše" od punog formalizma linearne algebre (nije posve općenito, niti su formalno definirani svi korišteni pojmovi), ono ni u tome obliku nije posve blisko i neposredno upotrebljivo za razumijevanje relevantnih koncepata u najčešćim fizikalnim i tehničkim primjenama (a oslanja se i na "matematičku" terminologiju i simbole koji nisu uobičajeni u tehnici). Zato se prije te "matematičke opcije" ukratko opisuje koncept koji je bliži praktičnom "tehničkom" poimanju. Operativni opis vektora za fizikalne i tehničke primjeneDok skalari imaju samo brojčanu vrijednost, vektori imaju iznos i smjer. Iznos vektora je brojčana vrijednost koja ne može biti negativna (npr. iznos brzine je 5 m/s), a smjer vektora možemo pokazati prstom (npr. gore, prema sjeveroistoku, itd). Takav je opis vektora ograničen na opažajni trodimenzionalni prostor. Tu su vektorske veličine brzina, sila, ubrzanje, količina gibanja... a skalarne masa, temperatura, obujam. Vektorska veličina obilježava se strelicom iznad simbola, npr. sila je (ili "masnim slovom", npr. F), dok se njezin iznos obilježava istim običnim slovom, npr. iznos sile je , jer se iz konteksta zna da to slovo označava silu koja je vektorska veličina. (U matematici se iznos vektora mora označiti vertikalnim crtama, npr. jer bi, općenito, slovo moglo označavati neku skalarnu veličinu koja nema veze s vektorima.) Vektor se grafički prikazuje pomoću usmjerene dužine (pomoću dužine koja ima strelicu na jednom kraju). Ona pokazuje smjer vektora, a njezina duljina je proporcionalna iznosu vektora. Umjesto načelne proporcionalnosti, iznos vektora može se grafički i precizirati, npr. tako da se naznači koliko njutna kod prikazane sile predstavlja 1 cm na skici. Neke se vektorske veličine doista i mjere u jedinicama za duljinu (npr. u centimetrima), pa ih usmjerena dužina u cjelosti opisuje (npr. vektor položaja ili radij-vektor, te vektor pomaka). Vektorske veličine u fizikalnim primjenama uglavnom su slobodni vektori ("pravi" vektori), no neke mogu biti vezani vektori ili pak klizni vektori. Primjerice, kad sila djeluje na deformabilno tijelo, njezin učinak ovisi o tome u kojoj točki zahvaća tijelo: ona je vezani vektor (vezan za tu točku koja se zove hvatište sile). Kad sila djeluje na kruto tijelo, njezin učinak ovisi o pravcu na kojemu leži, ali duž njega može po volji "klizati", pa je klizni vektor. Zato silu prikazujemo kao usmjerenu dužinu koja "počinje" (ili "završava") u svome hvatištu. Drugi primjer vezanog vektora je vektor položaja koji je usmjerena dužina povučena iz referentne točke (ishodišta). No, prilikom različitih matematičkih operacija sa silama i vektorima položaja (zbrajanje itd.), a kod većine drugih vektorskih veličina već i u samom prikazu, svejedno je gdje se pozicionira usmjerena dužina koja ih predstavlja: važan je samo iznos i smjer. To je svojstvo "slobodnih" ili "pravih" vektora: ako se usmjerena dužina paraleno premjesti u prostoru, ona i dalje predstavlja isti vektor. Zbrajanje vektora  Postupak zbrajanja vektora najlakše je intuitivno razumjeti na primjeru zbrajanja sila po pravilu paralelograma, koji je navodno bio poznat još u antičko doba, a eksplicitno ga spominju i Galileo i Newton.[1] U donjem dijelu lijeve skice prikazano je zbrajanje vektora i po pravilu paralelograma, a u gornjem dijelu isti rezultat je dobiven "nadovezivanjem" vektora. Očito je da su rezultati jednaki, jer je prikazani trokut identičan gornjoj polovici paralelograma (a jednako se mogla koristiti i donja polovica). Nadovezivanje mogućuje jednostavnije zbrajanje većeg broja vektora (skica desno): nadovezuju se jedan na drugoga, a zbroj je usmjerena dužina koja "ide" od početka prvoga do kraja zadnjega. I u jednom i u drugom primjeru zbrajanja, vektori su prikazani usmjerenim dužinama koje se mogu po volji translatirati (paralelno premještati) a da pritom i dalje predstavljaju iste vektore. Kod zbrajanja po paralelogramu, usmjerene dužine postavljaju se u istu početnu točku, a kod nadovezivanja početak druge se premješta u kraj prve. Važno je uočiti da rezultat ne ovisi o redoslijedu pribrojnika (zbrajanje vektora je komutativno), niti o njihovom grupiranju u slučaju više pribrojnika (zbrajanje vektora je asocijativno) zbog čega na skici desno nema zagrada u ispisu zbroja. Neke veličine, kojima se osim iznosa može pridružiti i smjer, nisu vektori jer ne zadovoljavaju ta svojstva vektorskog računa. Primjerice, kutu zakreta može se pridružiti isti smjer koji ima (prosječna) kutna brzina, što je vrlo prikladno za njegovo opisivanje u prostoru; ali kutovi zakreta nisu vektori, zato što njihov zbroj ovisi o redoslijedu zbrajanja. Rastavljanje vektora na komponente je obrnutii postupak od zbrajanja. Npr. za paralelogram sa lijeve skice može se smatrati i da prikazuje rastav vektora na komponente i . Rastavljanje vektora na komponente često je potrebno za razumijevanje njihove uloge, a i znatno olakšava račun.  Množenje vektora skalarom; suprotni vektorMnoženje vektora sa skalarom (brojem) je jednostavan postupak koji se intuitivno tumači na temelju zbrajanja vektora sa samim sobom: (taj rezultat se dobiva nadovezivanjem vektora na samoga sebe). Odatle se lako razumije poopćenje: kod množenje sa skalarom, množi se samo iznos vektora s apsolutnom vrijednošću skalara, a rezultat je vektor istoga smjera ako je skalar pozitivan, odnosno vektor suprotnog smjera ako je skalar negativan (skica desno). Specijalno, suprotni vektor od (vektor jednakog iznosa ali suprotnog smjera) je vektor koji se dobije množenjem vektora sa skalarom -1. Oduzimanje vektora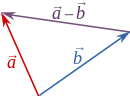 Oduzimanje vektora od vektora isto je što i dodavanje suprotnog vektora, tj. . Takav postupak grafički je prikazan niže u "matematičkom" dijelu teksta. U mnogim praktičnim primjenama, međutim, prikladnije je koristiti postupak prikazan na skici lijevo. Vektori na koje treba primijeniti oduzimanje grafički se prikažu pomoću usmjerenih dužina povučenih iz iste točke, a njihovu razliku prikazuje usmjerena dužina koja spaja njihove vrhove i koja ima smjer prema onome vektoru od kojega se drugi oduzima. Nije teško dokazati da usmjerena dužina doista jest tražena razlika: treba samo prinijeniti pravilo o zbrajanju vektora na prikazanu skicu. Skica se može interpretirati kao da prikazuje zbrajanje vektora , čiji rezultat očito mora biti (kad se makne zgrada) jednak vektoru , kao što crtež i pokazuje. Komponente vektora Za mnoge primjene korisno je rastaviti vektorske veličine na komponente u koordinatnom sustavu. Na skici desno prikazan je rastav sile u Kartezijevom sustavu x,y na dvije komponente. Njezine vektorske komponente su vektori paraleni s koordinatnim osima, i , tako da je:
Budući da su paralelne s koordinatnim osima, svaka od tih vektorskih komponenti može se opisati brojem (skalarom), kojim treba pomnožiti jedinični vektor odgovarajuće osi, ili . Jednični vektor ima iznos jednak jedinici i smjer pripadne osi, pa je: a brojevi i zovu se skalarne komponente vektora duž osi x odnosno y. Na skici desno vidi se da je Iz tako zadanih skalarnih komponenti, iznos vektora lako se izračuna pomoću Pitagorinog poučka a smjer se u ravnini x,y opisuje pomoću kuta prema jednoj od koordinatnih osi. Na skici je označen kut prema osi x, na način uobičajen u tehničkoj praksi (za razliku od matematike), kao neorijentirani kut manji od 90°. Taj se kut može odrediti pomoću tangensa omjera skalarnih komponenti. Obrnuto, ako bi bio poznat iznos vektora i kut , skalarne komponente za primjer sa skice računaju se kao gdje se predznak skalarne komponente određuje sa skice, jer su trigonometrijske funkcije kuta manjega od 90° pozitivne.  U mnogim je praktičnim situacijama moguće promatrati vektore i njihove komponente samo u jednoj ravnini, kao na gornjoj skici. No, često promatrani vektori ne leže u istoj ravnini, pa je potrebno računati s njihovim komponentama duž sve tri osi (skica lijevo). Postupak rastavljanja na komponente u načelu je sličan, mada ima malo više računanja. Vektor se pomoću skalarnih komponenti može zapisati na dva načina. Jedan je da se eksplicitno navedu jednični vektori koordinatnih osi, kako slijedi iz prethodnog opisa: Drugi način je pomoću uređene trojke brojeva: navode se samo skalarne komponente u redoslijedu x,y,z : U takvom zapisu, sila iz gornjeg ravninskog primjera prikazuje se kao
U općenitijem matematičkom opisu u n-dimenzionalnom prostoru, vektori se obično prikazuju pomoću uređenih n-torki, a brojevi u njima nazivaju se komponentama ili koordinatama vektora u nekoj bazi prostora. Prikaz vektora pomoću skalarnih komponenti u našem "običnom" prostoru značajno olakšava računanje. Vektori su jednaki ako su im jednake odgovarajuće skalarne komponente. Vektori se zbrajaju ili oduzimaju tako da se zbroje ili oduzmu njihove odgovarajuće skalarne komponente. I druge operacije među vektorima izražavaju se preko skalarnih komponenata, a različite jednadžbe među vektorima preslikavaju se u jednadžbe među njihovim skalarnim komponentama. Međusobno množenje vektoraU našem običnom prostoru, dva se vektora mogu međusobno množiti na dva načina, koji su se razvili ponajprije za potrebe jednostavnijeg zapisa odnosa među vektorskim veličinama u fizici, napose u mehanici. Skalarni produkt, ili skalarni umnožak, ili unutarnji produkt, ili in-produkt (na engleskom dot product, jer se obično piše pomoću točke između vektora) je operacija koja kao rezultat množenja dvaju vektora daje skalar (broj). Npr. za vektore i može se skalarni produkt definirati jednostavnim izrazom:
gdje je kut među vektorima, dok su i njihovi iznosi.  Vektorski produkt, ili vektorski umnožak, ili vanjski produkt, ili eks-produkt (jer se obično piše pomoću križića sličnoga znaku znaku x) je operacija koja kao rezultat množenja dvaju vektora (npr. vektora i ) daje treći vektor, okomit na njih oba, a smjer mu pobliže određuje pravilo desne ruke (skica desno). Umnožak (taj treći vektor) piše se kao , a izos mu je:
 Budući da je rezultat vektorskog množenje dvaju vektora opet vektor, on se može dalje množiti s nekim vektorom. Ako je to daljnje množenje vektorsko, dobije se trostruki vektorski produkt, npr:
Rezultat ovisi o položaju zagrada (tj. vektorsko množenje nije asocijativno). Usto, za razliku od skalarnog množenja, treba paziti i na redoslijed faktora u vektorskom množenju, jer se zamjenom mjesta dobija vektor suprotnog smjera (vektorsko množenje je antikomutativno). Trostruki produkt može se, naravno, i dalje vektorski množiti, pa se dobije četverostruki produkt, itd. Ako se vektorski produkt dvaju vektora pomnoži skalarno s trećim vektorom, dobije se mješoviti produkt. Na skici lijevo prikazano geometrijsko tumačenje mješovitog produkta
Iznos vektorskog produkta je, po definiciji, jednak površini paralelograma kojega određuju vektori i (obojan sivo, površina označena slovom A). Iznos skalarnog produkta vektora i jednak je umnošku te površine i projekcije vektora na vektor , koja je označena slovom h. Dakle, rezultat mješovitog produkta je volumen prikazane kose prizme, V=Ah. Neka važna svojstva množenja vektora, kao i zapis množenja pomoću skalarnih komponenata, navedeni su u "matematičkom" dijelu koji slijedi. Matematička definicija vektora u n-dimenzionalnom prostoruVektorske veličine su veličine određene s tri ili više parametara. Najpoznatiji su primjeri vezani za geometriju u prostoru gdje se vektor određuje pravcem, smjerom i intenzitetom (iznosom, veličinom, dužinom), a predstavlja strjelicom orijentiranom duž pravca, duljine proporcionalne intenzitetu, a čiji vrh pokazuje smjer na zadanom pravcu. Poopćeni vektor ne mora biti ograničen na tri dimenzije. Vektor može biti definiran uređenim parom točaka. Recimo da su to A i B iz Rn. Tada je:
Vektor se može predstaviti i polaznom točkom, jediničnim vektorom koji određuje njegov smjer i intenzitetom: Ako ovdje ||AB|| zamijenimo sa l koji može biti bilo koji broj iz R, definirali smo pravac koji prolazi kroz točku A a za vektor pravca ima vektor AB. Ukoliko je l samo nenegativno ili samo nepozitivno, definiran je polupravac, s početkom u točki A. Ukoliko je l neki broj različit od ||AB||, rezultat je vektor koji je s prethodnim kolinearan. Ako je novi vektor AB', tada vrijedi: Nul-vektorNul-vektor a0 je vektor čiji je intenzitet jednak nuli. Označuje se kao nula s naznakom za vektor. Jedinični vektorJedinični je vektor vektor čiji je intenzitet jednak jedinici. Za svaki se ne-nul vektor a može odrediti odgovarajući jedinični vektor v iste orijentacije i smjera. Ovaj se postupak zove normiranje vektora. Operacije nad vektorimaNad vektorima se, kao i svim ostalim elementima analitičke matematike, mogu uvesti aritmetičke operacije. Pri tome se vektor predstavlja kao uređena n-torka skalara koji pripadaju nekom polju K. Na primjer:
je jedan n-dimenzionalni vektor nad poljem K. Pojam n-dimenzionalni dolazi od činjenice da je vektor definiran pomoću n skalara. Prostor ovih vektora se još naziva Kn, a skalari koji čine vektor zajedno sa informacijom o njihovoj poziciji u uređenoj n-torci koordinate vektora. Na primjer, a1 je prva koordinata vektora, a2 je druga koordinata vektora itd. Slijede osnovne operacije nad vektorima, koje se u principu definiraju nad vektorima istih dimenzija. Intenzitet vektoraIntenzitet vektora se u euklidskoj geometriji definira kao kvadratni korijen zbroja kvadrata njegovih koordinata. Množenje vektora skalaromMnoženje vektora nekim skalarom je definirano kao množenje svake koordinate vektora tim skalarom. Ova je operacija komutativna.
Zbrajanje vektora  Uzmimo dva vektora : Njihovo se zbrajanje u principu definira kao zbrajanje komponenti sa istim indeksima.
Pri ćemu će vektor c biti iz prostora . Oduzimanje vektora bi se vršilo po sličnom principu: Pri čemu . Skalarno množenje vektoraSlično zbrajanju, skalarno se množenje vektora definira kao broj umnoška svih parova koordinata dva vektora, koje imaju iste indekse. Ovaj se zbroj i umnožak preuzimaju iz polja K. Razlika u odnosu na zbrajanje je ta što je rezultat skalarnog produkta dva vektora iz Kn u stvari jedan skalar iz K. Konkretno za dva vektora a i b iz Kn bi umnožak k izgledao ovako:
Ovdje treba primjetiti da je skalarni produkt vektora također jednak pri čemu je ω kut između a i b. Ovo zapravo znači i: To jest da su dva vektora okomiti ako im je skalarni produkt jednak nuli. Vektorski produktJoš jedan tip umnoška karakterističan za trodimenzionalne euklidske prostore (E3) je vektorski produkt. Definira se na sljedeći način: Jer su , i : vektori kanonske baze E3. Kod vektorskog je produkta bitno primjetiti sljedeće osobine:
Mješoviti produktMješoviti produkt vektora je ternarna matematička operacija koja uređenu trojku vektora iz E3 preslikava u skalar iz E. Zapisuje se sa A po definiciji je:
Što znači da je vrijednost mješovitog produkta tri vektora jednaka volumenu paralelepipeda kojeg oni oblikuju. Slijede neka osnovna svojstva mješovitog produkta: PovezanoIzvori
|






















































































![{\displaystyle [{\overrightarrow {a}},{\overrightarrow {b}},{\overrightarrow {c}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02bd06e6baf03173a720ab8030951b6fffede778)
![{\displaystyle [{\overrightarrow {a}},{\overrightarrow {b}},{\overrightarrow {c}}]=({\overrightarrow {a}}\times {\overrightarrow {b}})\cdot {\overrightarrow {c}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23aee79a7ddbb01c6a1bced056587e19911c4a6f)


![{\displaystyle [x,y,z]=-[y,x,z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/896fbb0f23e4c6b9c0b1986df2ee42d737eea67b)
![{\displaystyle [x,y,z]=[z,x,y]=[y,z,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81388e8d41317556dcfca17943da39fa476e7065)
![{\displaystyle [\alpha x,y,z]=\alpha [x,y,z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1dd715cbc57de6d39ba07a84cfb6726a6fcc726)
![{\displaystyle [x+t,y,z]=[x,y,z]+[t,y,z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a9245e888599afa2aa6083e986e54f3d4809ef8)














