Realan broj
|
Read other articles:

Artikel ini kemungkinan ditulis dari sudut pandang penggemar dan bukan sudut pandang netral. Mohon rapikan untuk menghasilkan standar kualitas yang lebih tinggi dan untuk membuat pemakaian nada yang netral. (Juni 2022) (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Topik artikel ini mungkin tidak memenuhi kriteria kelayakan biografi tokoh. Harap penuhi kelayakan artikel dengan: menyertakan sumber-sumber tepercaya yang independen terhadap subjek dan sebaiknya hindari sumbe...

Dekolonisasi Asia adalah perkembangan bertahap gerakan kemerdekaan di benua Asia, yang pada akhirnya menyebabkan hengkangnya kekuatan asing dan pembentukan sejumlah negara-bangsa di kawasan tersebut. Sejumlah peristiwa menjadi katalis perubahan ini, yang paling penting adalah Perang Dunia Kedua. Sebelum Perang Dunia II, beberapa negara seperti Filipina pada tahun 1898 telah memproklamasikan kemerdekaan dari Spanyol. Negara pertama yang didekolonisasi adalah Filipina pada tahun 1898, dan yang ...

Our School's E.T.Poster teatrikal untuk Our School's E.T.SutradaraPark Kwang-chunProduserChoi Yong-gi Park Bong-suDitulis olehChoi Jin-wonCeritaLee Hyeon-cheolPemeranKim Su-ro Lee Han-wi Kim Sung-ryung Baek Sung-hyun Park Bo-young Lee Min-ho Moon Chae-won Lee Chan-hoPenata musikChoi Man-sikSinematograferChoi Deok-kyuPenyuntingShin Min-kyungPerusahaanproduksiCourage FilmsDistributorSK TelecomFinecut (international)Tanggal rilis 11 September 2008 (2008-09-11) NegaraKorea SelatanBahas...

مسجد أدينة خان معلومات عامة الموقع شيراز[1] القرية أو المدينة شيراز الدولة إيران تعديل مصدري - تعديل مسجد أدينة خان (بالفارسية: مسجد آدینه خان) هو مسجد تاريخي يعود إلى عصر القاجاريون، ويقع في شيراز.[2] مراجع ^ Wiki Loves Monuments monuments database، 6 نوفمبر 2017، QID:Q28563569 ^ Encyclopa...

American-born Israeli historian and Nazi hunter (born 1948) Efraim ZuroffZuroff in 2007Born (1948-08-05) 5 August 1948 (age 75)[1]New York City, U.S.[1]NationalityAmerican, IsraeliAlma materYeshiva UniversityHebrew University of Jerusalem (PhD)[1]OccupationNazi hunterChildren4 Efraim Zuroff (Hebrew: אפרים זורוף; born August 5, 1948) is an American-born Israeli historian and Nazi hunter who has played a key role in bringing Nazi and fascist war crimi...

Chronologie de l'Europe 2007 en Roumanie - 2008 en Roumanie - 2009 en Roumanie - 2010 en Roumanie - 2011 en Roumanie 2007 par pays en Europe - 2008 par pays en Europe - 2009 par pays en Europe - 2010 par pays en Europe - 2011 par pays en Europe 2007 en Europe - 2008 en Europe - 2009 en Europe - 2010 en Europe - 2011 en Europe Chronologies Données clés 2006 2007 2008 2009 2010 2011 2012Décennies :1970 1980 1990 2000 2010 2020 2030Siècles :XIXe XXe XX...
Inability to reproduce by natural means This article is about the medical condition in humans. For the soil, see Soil fertility. Medical conditionInfertilitySpecialtyUrology, gynecologyCausesCommon in females: annouvulation, blocked fallopian tube, hormonal imbalance Common in males: low sperm count, abnormal sperm morphologyFrequency113 million (2015)[1] Infertility is the inability of an animal or plant to reproduce by natural means. It is usually not the natural state of a healthy ...

Pour les articles homonymes, voir Prévention routière (association) et Sécurité routière (organisme français). Silhouette indiquant le lieu d'un accident de piéton à des fins de sensibilisation à Stuttgart, en Allemagne. Trottoirs et feux de circulation dans Hagerstown (Maryland), États-Unis. Limites de vitesses dans différentes zones, affichant une limite « recommandée » de 130 km/h pour l'autoroute (Allemagne). Panneau à messages variables guidant la circulati...

لويجي أدملو معلومات شخصية الميلاد 30 أبريل 1764(1764-04-30)ميلانو الوفاة 11 فبراير 1849 (84 سنة)فلورنسا عضو في أكاديمية فنون الرسم الحياة العملية المدرسة الأم أكاديمية بريرا المهنة رسام اللغات الإيطالية تعديل مصدري - تعديل هذه المقالة يتيمة إذ تصل إليها مقالات أخرى ق�...

1959 British filmHigh JumpDirected byGodfrey GraysonWritten byBrian ClemensEldon HowardProduced byEdward J. DanzigerHarry Lee DanzigerStarringRichard WylerLisa DanielyLeigh MadisonCinematographyJames WilsonEdited byLee DoigProductioncompanyDanziger ProductionsDistributed byUnited Artists (UK)Release date 1959 (1959) Running time66 minutesCountryUnited KingdomLanguageEnglish High Jump is a low budget 1959 British crime film.[1] Plot A former trapeze artist becomes involved in a j...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها.Learn how and when to remove this message هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتع...
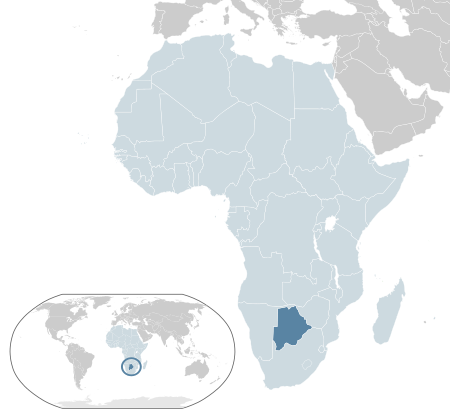
Country in Southern Africa This article is about the modern-day country. For the nominally-independent bantustan, see Bophuthatswana. Republic of BotswanaLefatshe la Botswana (Tswana) Flag Coat of arms Motto: PulaLet it RainAnthem: Fatshe leno la ronaBlessed Be This Noble LandShow globeShow map of AfricaCapitaland largest cityGaborone24°39.5′S 25°54.5′E / 24.6583°S 25.9083°E / -24.6583; 25.9083Official languagesEnglish[1]National lan...

A data storage tag (DST), also sometimes known as an archival tag, is a combination of a data logger and multiple sensors that record data at predetermined intervals. DSTs usually have a large memory size and a long lifetime: most are supported by batteries that allow the tag to record positions for several years. Alternatively some tags are solar powered and allow the scientist to set their own interval; this then allows data to be recorded for significantly longer than battery-only powered ...

لمعانٍ أخرى، طالع أمين أباد (توضيح). أمين أباد امين اباد - قرية - تقسيم إداري البلد إيران المحافظة مازندران المقاطعة مقاطعة آمل الناحية ناحية دابودشت القسم الريفي قسم دابوي الجنوبی الريفي إحداثيات 36°31′50″N 52°25′42″E / 36.53056°N 52.42833°E / 36.53056; 52.428...

Combined Statistical Area in Michigan, United StatesTri-CitiesCombined Statistical AreaSaginaw–Midland–Bay City, MICombined Statistical AreaFrom top to bottom: Saginaw, Midland, Bay CityNickname: Great Lakes Bay RegionMap of Saginaw–Midland–Bay City, MI CSA City of Saginaw Saginaw, MI MSA City of Midland Midland, MI MSA Bay City Bay City, MI MSA Coordinates: 42°10′21″N 85°21′09″W / &#x...

Park in Brooklyn, NY For other uses, see Holocaust memorial. This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: The Holocaust Memorial Park – news · newspapers · books · scholar · JSTOR (September 2020) (Learn how and when to remove this message) Holocaust Memorial Park Holocaust Memorial Park The Holocaust Memorial Park is a public Holocaust memorial park...

Johan Forssell Född16 mars 1855[1]Hökhuvuds församling[1], SverigeDöd18 september 1914[1][2] (59 år)Svedvi församling[1][2], SverigeBegravdKolbäcks kyrkogård[2]Medborgare iSverigeSysselsättningPolitiker[1][2], folkskollärare[1][2]BefattningAndrakammarledamot, Västmanlands läns södra domsagas valkrets (1903–1905)[1]Andrakammarledamot, Västmanlands läns södra domsagas valkrets (1909–1911)[1]Andrakammarledamot, Västmanlands läns västra valkrets (1912–1914)...

British Chambers of CommerceAbbreviationBCCFormation1860; 164 years ago (1860)Legal statusNot-for-profit organisationPurposeChambers of commerce in the UK, and UK businessLocationPetty FranceLondon, SW1United KingdomMembership 80,000Director-generalShevaun HavilandWebsitewww.britishchambers.org.uk The British Chambers of Commerce (BCC, formerly known prior to 1996 as the Association of British Chambers of Commerce[1]) is the national representative body of 53 chambe...

Francesco MoriniMorini in allenamento per la Juventus al Campo Combi nella stagione 1972-1973Nazionalità Italia Altezza185 cm Peso78 kg Calcio RuoloStopper Termine carriera1º dicembre 1980 CarrieraGiovanili 19??-1963 Sampdoria Squadre di club1 1963-1969 Sampdoria162 (0)[1]1969-1980 Juventus256 (0)1980 Toronto Blizzard22 (0) Nazionale 1973-1975 Italia11 (0) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo →...

1875 opera by Georges Bizet This article is about the opera. For other uses, see Carmen (disambiguation). CarmenOpera by Georges BizetPoster from the 1875 premièreLibrettist Ludovic Halévy Henri Meilhac LanguageFrenchBased onCarmenby Prosper MériméePremiere3 March 1875 (1875-03-03)Opéra-Comique, Paris Carmen (French: [kaʁmɛn] ⓘ) is an opera in four acts by the French composer Georges Bizet. The libretto was written by Henri Meilhac and Ludovic Halévy, based on...












































