Таблица Кэли
|
Read other articles:

Isole Vergini Britanniche ai Giochi della XXV OlimpiadeBarcellona 1992 Codice CIO IVB Comitato nazionale Comitato Olimpico delle Isole Vergini Britanniche Atleti partecipanti 4 in 2 discipline Di cui uomini/donne 4 - 0 Portabandiera Karl Scatliffe Medagliere Posizione - 0 0 0 0 Cronologia olimpica (sommario) Giochi olimpici estivi 1984 · 1988 · 1992 · 1996 · 2000 · 2004 · 2008 · 2012 · 2016 · 2020 Giochi olimpici invern...

1992 Hong Kong filmThe ShootoutFilm posterChinese nameTraditional Chinese危險情人Simplified Chinese危险情人TranscriptionsStandard MandarinHanyu PinyinWéi Xiǎn Qíng RénYue: CantoneseJyutpingNgai4 Him2 Cing4 Jan4 Directed byMichael MakScreenplay byEdward TangProduced byJackie ChanStarringAaron KwokFennie YuenBryan LeungSean LauElvis TsuiNgai SuetCinematographyEric ChuEdited byNg HungPeter CheungMusic byJoseph ChanProductioncompaniesGolden Harvest ProductionsGolden Way FilmsDis...

العلاقات التنزانية الطاجيكستانية تنزانيا طاجيكستان تنزانيا طاجيكستان تعديل مصدري - تعديل العلاقات التنزانية الطاجيكستانية هي العلاقات الثنائية التي تجمع بين تنزانيا وطاجيكستان.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية �...
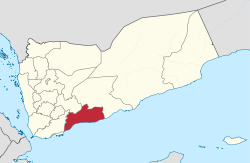
Governorate of Yemen Abyan redirects here. For the village in Iran, see Abyan, Iran. Governorate in Aden Region, YemenAbyan أَبْيَنْGovernorateCountry YemenRegionAden RegionSeatZinjibarArea • Total21,939 km2 (8,471 sq mi)Population (2012)[1] • Total513,701 • Density23/km2 (61/sq mi)Time zoneUTC+3 (Arabia Standard Time) Abyan (Arabic: أَبْيَنْ ʾAbyan) is a governorate of Yemen. The Abyan region was histo...

Former research initiative Human Microbiome Project (HMP)OwnerUS National Institutes of HealthEstablished2007 (2007)Disestablished2016 (2016)Websitehmpdacc.org The Human Microbiome Project (HMP) was a United States National Institutes of Health (NIH) research initiative to improve understanding of the microbiota involved in human health and disease. Launched in 2007,[1] the first phase (HMP1) focused on identifying and characterizing human microbiota. The second phase, known...

Pour les articles homonymes, voir Chapultepec (homonymie). Chapultepec Le monument des enfants héros. Géographie Pays Mexique Délégation Miguel Hidalgo Commune Mexico Superficie 6,86 km2 Localisation Coordonnées 19° 25′ 03″ nord, 99° 11′ 25″ ouest Géolocalisation sur la carte : Mexico Géolocalisation sur la carte : Mexique modifier Chapultepec est une colline et un grand parc, située à quelques kilomètres au sud-ouest du ...

Mitchell Donald Informasi pribadiNama lengkap Mitchell DonaldTanggal lahir 10 Desember 1988 (umur 35)Tempat lahir Nieuw-Vennep, BelandaTinggi 1,83 m (6 ft 0 in)Posisi bermain GelandangInformasi klubKlub saat ini Grafičar BeogradNomor 16Karier junior FC Bijlmer0000–1998 A.V.V. Zeeburgia1998–2007 AjaxKarier senior*Tahun Tim Tampil (Gol)2007–2011 Ajax 8 (1)2010 → Willem II (pinjaman) 14 (1)2011–2014 Roda JC Kerkrade 91 (12)2014–2015 FC Mordovia Saransk 14 (3)201...

White House Chief Usher This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Stephen W. Rochon – news · newspapers · books · scholar · JSTOR (December 2020) (Learn how and when to remove this message...

オットー・ニコライOtto Nicolai ヨーゼフ・クリーフーバー画(1842年)基本情報生誕 1810年6月9日 プロイセン王国、ケーニヒスベルク出身地 プロイセン王国、ケーニヒスベルク死没 (1849-05-11) 1849年5月11日(38歳没) プロイセン王国、ベルリンジャンル クラシック音楽職業 作曲家指揮者 ポータル クラシック音楽 カール・オットー・エーレンフリート・ニコライ(Carl Ott...

فريدريش إيبرت (بالألمانية: Friedrich Ebert) معلومات شخصية الميلاد 4 فبراير 1871 [1][2][3][4][5] هايدلبرغ[6] الوفاة 28 فبراير 1925 (54 سنة) [6][2][3][4] برلين[6] سبب الوفاة التهاب البريتون الإقامة بريمن مواطنة دوقية بادن الكبر�...

Parliamentary constituency in the United Kingdom HuddersfieldBorough constituencyfor the House of CommonsBoundary of Huddersfield in West YorkshireLocation of West Yorkshire within EnglandCountyWest YorkshireElectorate65,917 (December 2019)[1]Major settlementsHuddersfield, KirkheatonCurrent constituencyCreated1983Member of ParliamentBarry Sheerman (Labour Co-op)SeatsOneCreated fromHuddersfield EastHuddersfield West1832–1950SeatsOneType of constituencyBorough constituencyCreated from...

Canadian far-right political and social commentary media website Rebel Media redirects here. For the radio stations owned by an Australian company with the same name, see Rebel FM and The Breeze (Australia). Rebel NewsScreenshot Type of sitePoliticsAvailable inCanadian EnglishHeadquartersToronto, Ontario[1]OwnerEzra LevantFounder(s)Ezra Levant, Brian LilleyCEOEzra LevantKey peopleLawrence Solomon, Raheel Raza (Advisory Board)URLRebelNews.comCommercialYesRegistrationOptionalL...

Loosely defined region of Montana, U.S. Eastern Montana is a loosely defined region of Montana. Some definitions are more or less inclusive than others, ranging from the most inclusive, which would include the entire part of the state east of the Continental Divide, to the least inclusive, which places the beginning of eastern Montana roughly at or even east of Billings, Montana. The areas of Montana lying just east of the Continental Divide are often called Central Montana. A widely accepted...

Explosive weapon that utilizes nuclear reactions For other uses, see Atom bomb (disambiguation), A-bomb (disambiguation) or Nuke (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Nuclear weapon – news · newspapers · books · scholar · JSTOR (May 2022) (Learn how and when to remove this message...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أكتوبر 2022) سمير بنجلون معلومات شخصية الميلاد 7 فبراير 1985 (العمر 39 سنة)باريس الطول 1.80 م (5 قدم 11 بوصة) مركز اللعب مدافع الجنسية فرنسا المسيرة الاحترافية1 سن�...

قضاء الحر قضاء الحر الرياحي مرقد الحر الرياحي اللقب مدينة الحر الرياحي تاريخ التأسيس 1980م تقسيم إداري البلد العراق المحافظة محافظة كربلاء القضاء [محافظة كربلاء]] المسؤولون القائممقام حمود اليساري خصائص جغرافية إحداثيات 32°38′56″N 43°58′39″E / 32.6488138°N 43.9776365°E / 3...

لمعانٍ أخرى، طالع ييل (توضيح). ييل الإحداثيات 43°07′49″N 82°47′52″W / 43.130277777778°N 82.797777777778°W / 43.130277777778; -82.797777777778 [1] تاريخ التأسيس 1851 تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة سانت كلير خصائص جغرافية المساحة 3.601938...

Cláudio Hummes, O.F.M.cardinale di Santa Romana ChiesaIl cardinale Hummes il 28 novembre 2006. Omnes vos fratres Incarichi ricoperti Vescovo titolare di Carcabia (1975) Vescovo coadiutore di Santo André (1975) Vescovo di Santo André (1975-1996) Arcivescovo metropolita di Fortaleza (1996-1998) Arcivescovo metropolita di São Paulo (1998-2006) Gran priore per il Brasile-San Paolo dell'Ordine equestre del Santo Sepolcro di Gerusalemme (1998-2006) Cardinale presbitero di Sant'Antonio da ...

Perceived difference between the Eastern and Western worlds This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: East–West dichotomy – news · newspapers · books · scholar · JSTOR (November 2021) (Learn how and when to remove this message) East–West dichotomyA map highlighting the three easts as defined by Nea...

Set of related ordination techniques used in information visualization An example of classical multidimensional scaling applied to voting patterns in the United States House of Representatives. Each blue dot represents one Democrat member of the House, and each red dot one Republican. Part of a series on StatisticsData and information visualization Major dimensions Exploratory data analysis Information design Interactive data visualization Descriptive statistics Inferential statistics Statist...


