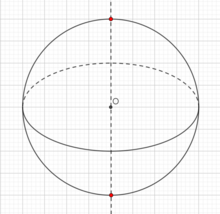
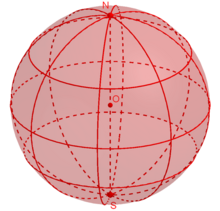
Сфера
|
Read other articles:

Strada statale 677di Ronchi dei LegionariLocalizzazioneStato Italia Regioni Friuli-Venezia Giulia DatiClassificazioneStrada statale InizioA4 uscita Redipuglia-Monfalcone Ovest FineAeroporto di Trieste-Ronchi dei Legionari Lunghezza2,028[1] km Data apertura1990[1] GestoreANAS (2005-2008)Friuli Venezia Giulia Strade (2008-) Manuale La strada statale 677 di Ronchi dei Legionari (SS 677) è una strada statale italiana di breve lunghezza. È una strada a quattro corsie, d...

Vous lisez un « article de qualité » labellisé en 2020. Pour les articles homonymes, voir Héraclius (homonymie). Héraclius Empereur byzantin Solidus à l'effigie d'Héraclius et de ses fils Constantin III et Héraclonas. Règne 5 octobre 610-11 février 641 30 ans, 4 mois et 6 jours Période Héraclides Précédé par Phocas Suivi de Constantin III HéracliusHéraclonas Biographie Nom de naissance Flavius Heraclius Naissance vers ou en 575 Cappadoce Décès 11 ...
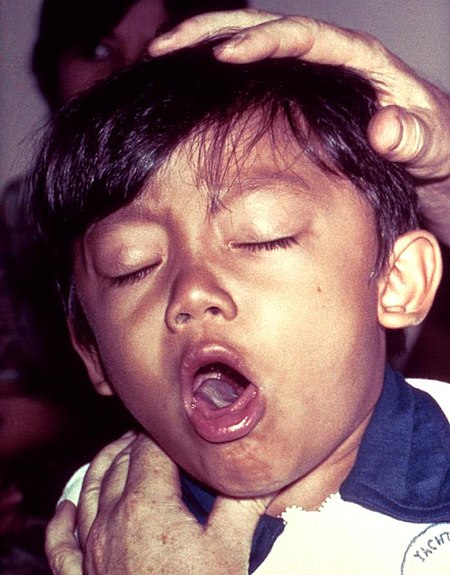
BatukSeorang anak yang mengidap batuk rejan. Coughing The sound of a person coughing. Bermasalah memainkan berkas ini? Lihat bantuan media. Informasi umum Batuk adalah mekanisme pertahanan tubuh pada sistem pernapasan. Terjadinya batuk hanya merupakan gejala dari suatu penyakit atau reaksi tubuh terhadap gangguan pada saluran pernapasan oleh berbagai benda asing yang masuk ke dalamnya. Batuk terjadi karena rangsangan tertentu. Terjadinya batuk merupakan gejala awal bagi penyakit influenza dan...

Aino KishiNama asal希志あいのLahir1 Februari 1988 (umur 36)Hokkaido, JepangKebangsaan JapanPekerjaanAktris Tahun aktif2008–2015Tinggi156 cm (5 ft 1 in)Situs webwww.duo-official.com/models/aino-kishi.htmTanda tangan Aino Kishi (希志あいのcode: ja is deprecated , Kishi Aino, lahir 1 Februari 1988),[1] adalah seorang aktris, penyanyi dan mantan AV idol asal Jepang. Kishi memulai karirnya pada tahun 2008, Kishi membintangi lebih dari 400 fil...

Koordinat: 8°42′S 115°27′E / 8.7°S 115.45°E / -8.7; 115.45 Nusa Ceningan pada tahun 2009 Nusa Ceningan adalah sebuah pulau kecil yang merupakan salah bagian satu pulau dari tiga gugusan kepulaun di Nusa Penida. Berdasarkan hasil pemetaan partisifatif yang pernah dilakukan oleh masyarakat bekerja beberapa lembaga LSM pada tahun 2000, luas pulau Ceningan adalah 300,6 Ha, yang terdiri dari 2 Dusun (sekarang banjar Dinas) yaitu Dusun Ceningan Kawan dan Dusun Cening...

Serie D 2022-2023 Competizione Serie D Sport Calcio Edizione 75ª Organizzatore Lega Nazionale DilettantiDipartimento Interregionale Date dal 3 settembre 2022al 7 maggio 2023 Luogo Italia Partecipanti 166 Formula 9 gironi con play-off Sito web http://seried.lnd.it/it/serie-d Risultati Vincitore Sestri Levante(1º titolo) Altre promozioni LumezzaneLegnagoGiana ErminioArezzoPinetoSorrentoBrindisiCataniaCasertana Retrocessioni Castanese, Stresa Vergante, Casale, Fossano; Seregno, ...

Airport in Tamchy, KyrgyzstanIssyk-Kul International AirportЫсык-Көл эл аралык аэропортуIATA: IKU (ИКУ)ICAO: UCFLSummaryAirport typePublicOperatorGovernmentServesTamchyLocationTamchy, KyrgyzstanHub forKyrgyzstan Air CompanyElevation AMSL5,426 ft / 1,653 mCoordinates42°35′8″N 76°42′25″E / 42.58556°N 76.70694°E / 42.58556; 76.70694MapIKURunways Direction Length Surface m ft 07/25 3,800 12,467 Asphalt [1] Issyk...

For data relating to SSSIs in this Area of Search see List of Sites of Special Scientific Interest in Conwy, Denbighshire, Flintshire, and Wrexham. Clwyd AOS SSSIs in the UK are notified using the concept of an Area of Search (AOS), an area of between 400 km2 (150 sq mi) and 4,000 km2 (1,500 sq mi) in size.[1] The Areas of Search were conceived and developed between 1975 and 1979 by the Nature Conservancy Council (NCC), based on regions creat...

American record executive Mack MaineBirth nameJermaine Anthony PreyanBorn (1982-07-28) July 28, 1982 (age 41)OriginNew Orleans, Louisiana, U.S.GenresHip hopOccupation(s) Record executive songwriter rapper Years active2003–presentLabelsSoothe Your SoulRepublicYoung MoneyCash MoneyUniversal MotownMusical artist Jermaine Anthony Preyan (born January 15, 1982), better known by his stage name Mack Maine, is an American record executive, songwriter, and rapper from New Orleans, Louisiana. He...

2011 film The 5th QuarterTheatrical release posterDirected byRick BieberWritten byRick BieberBased onJon Abbate and the 2006 Wake Forest Demon Deacons football teamProduced byRick Bieber[1]Starring Aidan Quinn Andie MacDowell Ryan Merriman CinematographyCraig HaagensenEdited byMark ConteMusic byAndy MendelsonProductioncompanies 5th Quarter Park Entertainment Distributed byRocky Mountain PicturesRelease date March 25, 2011 (2011-03-25) Running time101 minutesCountryUnite...

Daerah ini tidak sama dengan Albania di Eropa tenggara. Negara kuno Kaukasus: Armenia, Iberia, Colchis dan Albania Albania Kaukasia, juga disebut Alvank dalam bahasa Armenia,[1][2] Ardhan dalam bahasa Parthia, Arran dalam bahasa Persia,[3] dan Al-Ran dalam bahasa Arab,[1][3] adalah kerajaan kuno yang terletak di daerah Republik Azerbaijan dan Dagestan selatan modern. Nama Albania adalah nama dalam bahasa Latin, dan istilah untuk tanah bergunung-gunung.&...

Minor league baseball teamTrenton ThunderFounded in 1994 Trenton, New Jersey Team logo Cap insignia Minor league affiliationsClassCollegiate summer (2021–present)Previous classesDouble-A (1994–2020)LeagueMLB Draft League (2021–present)Previous leaguesEastern League (1994–2020)Major league affiliationsTeamUnaffiliated (2021–present)Previous teams New York Yankees (2003–2020) Boston Red Sox (1995–2002) Detroit Tigers (1994) Minor league titlesLeague titles (5)20072008201320192021D...

Play by Christopher Marlowe This article is about the play by Christopher Marlowe. For other uses, see Doctor Faustus. The Tragical History of the Life and Death of Doctor FaustusFrontispiece to a 1620 printing of Doctor Faustus showing Faustus conjuring Mephistophilis. The spelling Histoy is agreed to be a typographical error.[1]Written byChristopher MarloweCharactersDoctor Faustus Lucifer Mephistophilis Belzebub Seven deadly sins Pope Adrian VI Charles V Duke of Saxony Helen of Troy...

В Википедии есть статьи о других людях с фамилией Коннелл. В другом языковом разделе есть более полная статья Richard Connell (англ.). Вы можете помочь проекту, расширив текущую статью с помощью перевода Ричард КоннеллRichard Edward Connell Jr. Дата рождения 17 октября 1893(1893-10-17)[1][2]...

Pour des articles plus généraux, voir Histoire de la Suisse depuis 1914, Seconde Guerre mondiale et Opération Tannenbaum. Buste du général Henri Guisan à Avenches. L'histoire de la Suisse pendant la Seconde Guerre mondiale a lieu de manière indirecte. La Suisse n'a pas été occupée pendant la Seconde Guerre mondiale ni par les membres de l'Axe ni par les Alliés, malgré le haut risque d'une invasion de celle-ci le 24 juin 1940 par l'Allemagne nazie, qui planifia l'opération Tannen...

В Википедии есть статьи о других людях с фамилиями Погодин и Стукалов. В Википедии есть статьи о других людях с такими же именем, отчеством и фамилией: Погодин, Николай Фёдорович. Николай Фёдорович Погодин Имя при рождении Николай Фёдорович Стукалов Псевдонимы Погодин Да...

نسبة مئويةمعلومات عامةالنوع ترميز جزء-في — dimensionless unit (en) — وحدة مشتقة من UCUM — unit of dimensionless quantity (en) تستخدم لقياس كمية لا بعدية رمز الوحدة القائمة ... % (بالإنجليزية) % (بالفرنسية) % (بالأذرية) % (بالكتالونية) % (بالبيلاروسية) % (بالأوكرانية) % (بالروسية) % (بالبولندية) تحويلات الوحد...

Richard Dix Información personalNombre de nacimiento Ernst Carlton BrimmerNacimiento 18 de julio de 1893 St. Paul (Minnesota), Estados Unidos de AméricaFallecimiento 20 de septiembre de 1949 (56 años) Los Ángeles, California, Estados Unidos de AméricaCausa de muerte Infarto agudo de miocardio Sepultura Forest Lawn Memorial Park Nacionalidad EstadounidenseLengua materna Inglés FamiliaCónyuge Winifred Coe (1931-1933) Virginia Webster (1934-1949)EducaciónEducado en Universidad de Minneso...

1946 1956 Élections législatives de 1951 dans l'Aisne 6 sièges de députés à l'Assemblée nationale 17 juin 1951 Type d’élection Élections législatives Corps électoral et résultats Population 453 411 Votants 226 277 84,72 % 3,5 Adrien Renard – Parti communiste Voix 73 888 33,53 % 4,7 Députés élus 2 1 Edmond Bricout – RPF Voix 45 521 20,66 % 7,6 Députés élus 1 Mar...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne s'appuie pas, ou pas assez, sur des sources secondaires ou tertiaires (mars 2013). Pour améliorer la vérifiabilité de l'article ainsi que son intérêt encyclopédique, il est nécessaire, quand des sources primaires sont citées, de les associer à des analyses faites par des sources secondaires. Une machine de Turing quelconque M réalise un calcul à partir d'une entrée écrite sur son ruban...










![{\displaystyle \theta \in [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c833964ea08aa30df8b6f56664461a5499b38144)








![{\displaystyle A_{x}=(x_{1}^{2}+y_{1}^{2}+z_{1}^{2})[y_{2}(z_{3}-z_{4})+y_{3}(z_{4}-z_{2})+y_{4}(z_{2}-z_{3})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98aeceefde815d50b9c88071fd5af521cebcbd9b)
![{\displaystyle B_{x}=(x_{2}^{2}+y_{2}^{2}+z_{2}^{2})[y_{3}(z_{4}-z_{1})+y_{4}(z_{1}-z_{3})+y_{1}(z_{3}-z_{4})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e8fd51ac73a6f9738ad21bab83bc95106a37419)
![{\displaystyle C_{x}=(x_{3}^{2}+y_{3}^{2}+z_{3}^{2})[y_{4}(z_{1}-z_{2})+y_{1}(z_{2}-z_{4})+y_{2}(z_{4}-z_{1})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8949e7118a516802283f47c40671877d166e202d)
![{\displaystyle D_{x}=(x_{4}^{2}+y_{4}^{2}+z_{4}^{2})[y_{1}(z_{2}-z_{3})+y_{2}(z_{3}-z_{1})+y_{3}(z_{1}-z_{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1eb66cc2d861cb44c430b1d4d444669e7d64ac50)
![{\displaystyle A_{y}=(x_{1}^{2}+y_{1}^{2}+z_{1}^{2})[z_{2}(x_{3}-x_{4})+z_{3}(x_{4}-x_{2})+z_{4}(x_{2}-x_{3})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0596cda990bc94b1c25e2dd59597025782fff0bc)
![{\displaystyle B_{y}=(x_{2}^{2}+y_{2}^{2}+z_{2}^{2})[z_{3}(x_{4}-x_{1})+z_{4}(x_{1}-x_{3})+z_{1}(x_{3}-x_{4})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df7dda4bc308cb263a2b6fad07eee8b52afec515)
![{\displaystyle C_{y}=(x_{3}^{2}+y_{3}^{2}+z_{3}^{2})[z_{4}(x_{1}-x_{2})+z_{1}(x_{2}-x_{4})+z_{2}(x_{4}-x_{1})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37e51cd29b0a770dbee0da4ecae0485674fb0147)
![{\displaystyle D_{y}=(x_{4}^{2}+y_{4}^{2}+z_{4}^{2})[z_{1}(x_{2}-x_{3})+z_{2}(x_{3}-x_{1})+z_{3}(x_{1}-x_{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75a4d722990be4e16b53049151c2c60670fe1f9a)
![{\displaystyle A_{z}=(x_{1}^{2}+y_{1}^{2}+z_{1}^{2})[x_{2}(y_{3}-y_{4})+x_{3}(y_{4}-y_{2})+x_{4}(y_{2}-y_{3})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36e18121f2b8cbbc0ba2a2471618f1595185f5dc)
![{\displaystyle B_{z}=(x_{2}^{2}+y_{2}^{2}+z_{2}^{2})[x_{3}(y_{4}-y_{1})+x_{4}(y_{1}-y_{3})+x_{1}(y_{3}-y_{4})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aaf9dd4dead678b833a04a999c97feb8f9357d4b)
![{\displaystyle C_{z}=(x_{3}^{2}+y_{3}^{2}+z_{3}^{2})[x_{4}(y_{1}-y_{2})+x_{1}(y_{2}-y_{4})+x_{2}(y_{4}-y_{1})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef5b67f4a5c22bce5874484e51f088679438eef3)
![{\displaystyle D_{z}=(x_{4}^{2}+y_{4}^{2}+z_{4}^{2})[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d904f3b36dc6b2cd7249cca7db350f3895ef61b6)
















