Начальный объект
|
Read other articles:

Keuskupan TagumDiœcesis TagamnaDiyosesis ng TagumKatolik Katedral Kristus RajaLokasiNegara FilipinaWilayahDavao del Norte (kecuali Samal), dan Lembah CompostelaProvinsi gerejawiDavaoStatistikLuas8.129 km2 (3.139 sq mi)Populasi- Total- Katolik(per 2014)1.595.0001,431,000 (89.7%)Paroki27Imam97InformasiDenominasiKatolik RomaGereja sui iurisGereja LatinRitusRitus RomaPendirian13 Januari 1962 (sebagai Prelatur)11 Oktober 1980 (sebagai Keuskupan)KatedralKate...

Le Petit PrincePoster teaser PrancisSutradaraMark OsborneProduserAton Soumache Dimitri RassamSkenarioIrena BrignullBerdasarkanLe Petit Princeoleh Antoine de Saint-ExupéryPemeranRiley Osborne Marion Cotillard Mackenzie Foy James Franco Rachel McAdams Jeff Bridges Benicio del Toro Paul Giamatti Albert Brooks Matt JenkinsPenata musikHans ZimmerPenyuntingCarole Kravetz Aykanian, Matthew LandonPerusahaanproduksiOnyx FilmsDistributorParamount Vantage (AS)Entertainment One (Kanada)Paramount P...

Pour les articles homonymes, voir Obradović. Dositej ObradovićPortrait par Arsa TeodorovićFonctionMinistre de l'Éducation (en)BiographieNaissance Vers 1739Ciacova (Empire d'Autriche)Décès 28 mars 1811Belgrade (Principauté de Serbie)Sépulture Cathédrale Saint-Michel de BelgradeNom de naissance Dimitrije ObradovićNationalité autrichienneActivités Linguiste, écrivain, poète, philosopheAutres informationsA travaillé pour Université de BelgradeSignatureVue de la sépulture.modifie...

Questa voce sull'argomento attori indiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Jagdeep (2010) Jagdeep, pseudonimo di Syed Ishtiaq Ahmed Jaffrey (Datia, 29 marzo 1939 – Mumbai, 8 luglio 2020), è stato un attore indiano. Biografia Nella sua carriera, cominciata nel 1950, prese parte a circa 390 tra produzione cinematografiche e televisive. Aveva all'attivo anche un film da regista e sceneggiatore datato 1988. Morì nell'estate del 2020, la...

Mary Fallin pada Mei 2015 Mary Fallin /ˈfælɪn/ (née Copeland; lahir 9 Desember 1954)[1] adalah seorang politikus Amerika Serikat yang menjabat sebagai gubernur Oklahoma ke-27 dari 2011 sampai 2019. Sebagai anggota Partai Republik, ia terpilih pada 2010 dan terpilih lagi pada 2014. Referensi ^ Wilson, Linda D. Fallin, Mary Newt Copeland. Oklahoma Historical Society. Diakses tanggal July 18, 2018. Pranala luar Wikimedia Commons memiliki media mengenai Mary Fallin. Governor Mar...

Radio alert system from ground communicators for aircrew Not to be confused with Selcall. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) Some of this article's listed sources may not be reliable. Please help improve this article by looking for better, more reliable sources. Unreliable citations may be challenged and removed. (November 2021) (Learn how and when to remove this message) Thi...

Sri Lankan cricketer This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Mahela Jayawardene – news · newspapers · books · scholar · JSTOR (May 2017) (Learn how and when to remove this message) Mahel...

صلاح الدين المنجد معلومات شخصية تاريخ الميلاد 1920 تاريخ الوفاة 2010 عضو في مجمع اللغة العربية بدمشق الحياة العملية المهنة كاتب أعمال بارزة المستظرف من أخبار الجواري (الكتاب الجديد، 1976) [لغات أخرى]، والمستشرقون الألمان: تراجمهم وما أسهموا به في الدراسات ال�...

Presiding officer of the United States House of Representatives For a list of speakers of the House, see List of speakers of the United States House of Representatives. Speaker of the United States House of RepresentativesSeal of the speakerIncumbentMike Johnsonsince October 25, 2023United States House of RepresentativesStyle Mr. Speaker (informal – male) Madam Speaker (informal – female) The Honorable (formal) StatusPresiding officerSeatUnited States Capitol, Washington, D.C.Nominat...
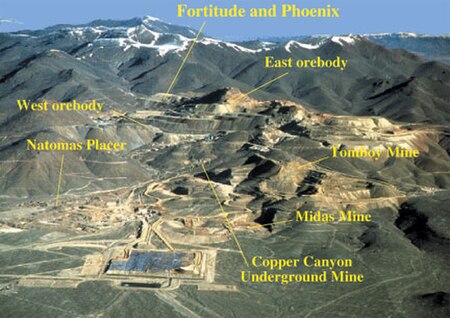
Mountain range in Lander and Humboldt counties of Nevada, USA Battle Mountains, NevadaBattle Mountains in Nevada Highest pointPeakNorth Peak, Humboldt CountyElevation2,606 m (8,550 ft)Coordinates40°40′30″N 117°07′57″W / 40.67500°N 117.13250°W / 40.67500; -117.13250[1]DimensionsLength24 km (15 mi) N-SWidth22 km (14 mi) E-WArea337 km2 (130 sq mi)[2]GeographyCountryUnited StatesState...

American journalist (born 1963) Dan FaginFagin at the 2015 Texas Book FestivalBorn (1963-02-01) February 1, 1963 (age 61)Oklahoma City, Oklahoma, U.S.OccupationEnvironmental journalist, New York University journalism professorNationalityAmericanEducationDartmouth CollegeNotable awardsPulitzer Prize for General Nonfiction (2014)WebsiteDanFagin.com Dan Fagin (born February 1, 1963) is an American journalist who specializes in environmental science. He won the 2014 Pulitzer Prize for Genera...

Island in the Pacific Ocean Farallon de MedinillaNOAA photo of Farallon de MedinillaGeographyLocationPacific OceanCoordinates16°1′2″N 146°3′31″E / 16.01722°N 146.05861°E / 16.01722; 146.05861ArchipelagoNorthern Mariana IslandsArea0.35 sq mi (0.91 km2)[1]Length2.8 km (1.74 mi)Width0.5 km (0.31 mi)Highest elevation81 m (266 ft)AdministrationUnited StatesCommonwealthNorthern Mariana IslandsDemographicsP...

ملك إسواتيني الحالي ملك إسواتيني الملك مسواتي الثالث ملك إسواتيني الحالي فترة الحكم25 أبريل، 1986 – الآن تاريخ التتويج 25 أبريل، 1986 معلومات شخصية الاسم الكامل ماغتزيف دلاميني الميلاد 19 أبريل 1968إسواتيني الأب سوبوزا الثاني الأم انتونبي تعديل مصدري - تعديل هذه الصفحة تحتوي...

Questa voce sull'argomento geografia degli Stati Uniti d'America è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Stati centrali del sud-ovestMappa dinamica degli Stati Uniti meridionali che evidenzia le varie sottoclassificazioni storiche, culturali e censuarie Stati Arkansas Louisiana Oklahoma Texas Superficie1 150 089,4 km² Abitanti40 619 450 (2019) Densità35 ab./km² Stati centrali del sud-ov...

F3D SkyknightSebuah EF-10B Skyknight dari VMCJ-2 PlayboysTipePesawat tempurTerbang perdana23 Maret 1948Diperkenalkan1951Dipensiunkan1970Pengguna utamaAngkatan Laut Amerika SerikatPengguna lainKorps Marinir Amerika SerikatJumlah produksi265 Douglas F3D Skyknight, (kemudian F-10 Skyknight) merupakan sebuah pesawat tempur bermesin kembar, yang dikeluarkan oleh Douglas Aircraft Company di El Segundo, California, Amerika Serikat. F3D telah dirancang sebagai sebuah pesawat semua kondisi cuaca untuk...

提示:此条目页的主题不是西方阿拉伯数字或阿拉伯字母数字。 当代埃及电话按钮。 數制记数系统 进位制 印阿體系 西方阿拉伯數字 阿拉伯文数字 孟加拉数字 印度數字 Gujarati(英语:Gujarati numerals) 古木基文 Odia(英语:Odia numerals) Sinhala(英语:Sinhala numerals) Tamil(英语:Tamil numerals) Malayalam(英语:Malayalam numerals) 泰卢固文 卡納達文 Dzongkha(英语:Dzongkha n...

Celtic language spoken in France BretonbrezhonegBilingual sign in Huelgoat in BrittanyPronunciation[bʁeˈzɔ̃ːnɛk], [brəhɔ̃ˈnek]Native toBrittany (France)RegionLower BrittanyEthnicityBretonsNative speakers210,000 in Brittany (2018)[1]16,000 in Île-de-France[2](Number includes students in bilingual education)[3]Language familyIndo-European CelticInsular CelticBrittonicSouthwestern BrittonicBretonEarly formsOld Breton Middle Breton Dial...

「うす」はこの項目へ転送されています。漢字の部首については「臼部」をご覧ください。 臼(うす、舂)とは、製粉や脱稃に用いる道具である。 トウモロコシ、麦や米など、人類の主食である穀物を調理するにあたっては、そのまま食する粒食と、いったん粉末に粉砕してからパンなどの食品に加工する粉食文化がある。世界の大部分は粉食文化圏に属し、臼は粉�...

「陸風」はこの項目へ転送されています。大日本帝国海軍が計画した戦闘機については「二十試甲戦闘機」をご覧ください。 湾口(写真奥)から陸(手前)へ吹く海風によりさざなみが立った水面(オーストラリア・ホバート) 海陸風(かいりくふう)とは海岸地帯に見られる風であり、昼は海から陸へ吹く海風、夜は陸から海へ吹く陸風というように、風向が変化�...
この項目では、かつて存在した法人について説明しています。一般名詞としての民生産業については「民生用」をご覧ください。 この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 民生産業 – ニュース · 書籍 · スカラー ...





















