Кантор, Георг
| |||||||||||||||||||||||||||||||||||||||
Read other articles:

Katedral Campo MaiorKatedral Santo AntoniusCatedral Santo AntônioKatedral Campo MaiorLokasiCampo MaiorNegaraBrasilDenominasiGereja Katolik RomaArsitekturStatusKatedralStatus fungsionalAktifAdministrasiKeuskupanKeuskupan Campo Maior Katedral Campo Maior yang bernama resmi Katedral Santo Antonius (Portugis: Catedral Santo Antôniocode: pt is deprecated ) adalah sebuah gereja katedral Katolik yang terletak di Lapangan Bona Primo di Campo Maior,[1] di negara bagian Piauí[2] bagi...

Bangku dan meja kayu di depan sebuah warung makan. Bangku atau lincak adalah sebuah mebel tempat duduk berkaki serupa kursi dengan dudukan lebih panjang.[1] Bangku biasanya diduduki untuk beristirahat, bersantap, berkencan, atau menongkrong sambil mengobrol. Bangku umumnya diletakkan di tempat-tempat seperti kawasan pejalan kaki, tempat wisata, pertokoan, tempat makan, maupun taman kota. Bangku umumnya terbuat dari logam dan kayu (terkadang dikombinasikan juga dengan logam). Namun ter...

AwakeAlbum studio karya Josh GrobanDirilis7 November 2006GenrePop / Classical / VocalLabelReprise Records / 143 RecordsKronologi Josh Groban Closer(2003)Closer2003 Awake(2006) Noël(2007)Noël2007 Awake adalah album dari penyanyi Amerika Serikat, Josh Groban. Album ini dirilis 7 November 2006. Single pertama dari album ini adalah You Are Loved (Don't Give Up). Daftar lagu Mai (Leo Z./Andrew Sandri/Marco Marinangeli) - 4:35 You Are Loved (Don't Give Up) (Thomas Salter) - first single - 4:4...

Sekolah Staf dan KomandoAngkatan UdaraLambang SeskoauDibentuk1 Agustus 1963Negara IndonesiaCabang TNI Angkatan UdaraTipe unitKomando PendidikanBagian dariSesko TNIMarkasLembang, Bandung Barat, Jawa BaratMotoPragnya Paramartha JayaSitus websesko.tni-au.mil.idTokohKomandanMarsekal Muda TNI Minggit Tribowo, S.IP.Wakil KomandanMarsekal Pertama TNI Tahyodi, S.A.P.Kepala Koordinator DosenMarsekal Pertama TNI Eduard Sri Wisnu Murendro, S.E. Sekolah Staf dan Komando Angkatan Udara (Seskoau) adal...

Mathematical tree in the hyperbolic plane A hyperbolic tree (often shortened as hypertree) is an information visualization and graph drawing method inspired by hyperbolic geometry. A basic hyperbolic tree. Nodes in focus are placed in the center and given more room, while out-of-focus nodes are compressed near the boundaries. Focusing on a different node brings it and its children to the center of the disk, while uninteresting portions of the tree are compressed. Displaying hierarchical data ...

Book by L.A. Meyer This article's plot summary may be too long or excessively detailed. Please help improve it by removing unnecessary details and making it more concise. (May 2015) (Learn how and when to remove this template message) The Wake of the Lorelei Lee First editionAuthorL.A. MeyerAudio read byKatherine KellgrenCountryUnited StatesLanguageEnglishGenreYoung adult, Historical novelPublished2010PublisherHoughton Mifflin HarcourtPages552 pagesISBN9780547327686Preceded byR...
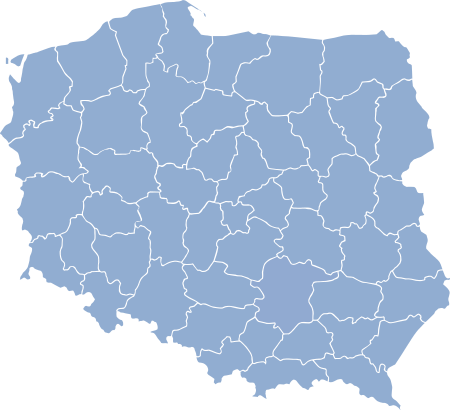
This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Płock Voivodeship 1975–1998 – news · newspapers · books · scholar · JSTOR (August 2009) (Learn how and when to remove this template message) Płock Voivodeship (Polish: województwo płockie) was a unit of administrative division and local government in Poland from 1975 ...

CE1 DT16 Stasiun MRT Bayfront海湾地铁站பேஃபுரெண்ட்Angkutan cepatLokasi12A Bayfront Avenue Singapore 018970Koordinat1°16′56″N 103°51′34″E / 1.282347°N 103.859317°E / 1.282347; 103.859317Jalur Jalur Lingkar Jalur Pusat Kota Jumlah peronPulau susunJumlah jalur4LayananBus, TaksiKonstruksiJenis strukturBawah tanahTinggi peron3Akses difabelYesInformasi lainKode stasiunCE1 / DT16SejarahDibukaD...

Bahasa Gaya Kaya, Karak, Kara Dituturkan diKonfederasi GayaWilayahSemenanjung KoreaEraabad ke-5 hingga ke-7 Rumpun bahasatidak terklasifikasi, kemungkinan Japonik? atau Koreanik? Kode bahasaISO 639-3zraLINGUIST ListzraGlottologTidak adaQIDQ5528695 Status konservasi Punah EXSingkatan dari Extinct (Punah)Terancam CRSingkatan dari Critically endangered (Terancam Kritis) SESingkatan dari Severely endangered (Terancam berat) DESingkatan dari Devinitely endangered (Terancam) VUSingkatan dari V...

Bodo SpranzBorn(1920-01-01)1 January 1920NordhausenDied1 September 2007(2007-09-01) (aged 87)BremenAwardsKnight's Cross of the Iron Cross with Oak LeavesAcademic workMain interestsPreclassic meso-American history Bodo Spranz (1 January 1920 – 1 September 2007) was a German researcher of preclassic meso-American history and director of the ethnological museum in Freiburg. During World War II he was a hauptmann in the Wehrmacht of Nazi Germany receiving the Knight's Cross of the Iron Cro...

The CombineTokoh seri Half-LifeSimbol penjepit dari Combine, yang terlihat di Half-Life 2 dan Half-Life: Alyx sebagai simbol propaganda mereka.PenampilanperdanaHalf-Life 2 (2004) The Combine (pengejaan: /ˈkɒmbaɪn/ KOM-byne), atau disebut juga sebagai Universal Union adalah kerajaan multidimensi fiksi yang merupakan antagonis dalam seri Half-Life oleh Valve Corporation. Referensi Pranala luar The Combine at Combine OverWiki, a Half-Life Wikia lbsSeri Half-Life dan topik berkaitSerial utamaH...

Questa voce sull'argomento contee dell'Illinois è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Contea di LawrenceconteaLocalizzazioneStato Stati Uniti Stato federato Illinois AmministrazioneCapoluogoLawrenceville Data di istituzione1821 TerritorioCoordinatedel capoluogo38°43′12″N 87°43′48″W / 38.72°N 87.73°W38.72; -87.73 (Contea di Lawrence)Coordinate: 38°43′12″N 87°43′48″W / 38.72°N ...

Jan de Bont nel 1973 Jan de Bont (Eindhoven, 22 ottobre 1943) è un direttore della fotografia, regista e produttore cinematografico olandese. Inizio la carriera cinematografica come direttore della fotografia e poi diresse film blockbuster come Speed (1994) e Twister (1996). Indice 1 Biografia 2 Filmografia 2.1 Regista 2.2 Direttore della fotografia 3 Altri progetti 4 Collegamenti esterni Biografia Proviene da una famiglia cattolica composta da 17 figli. Si crea un nome come direttore della ...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...
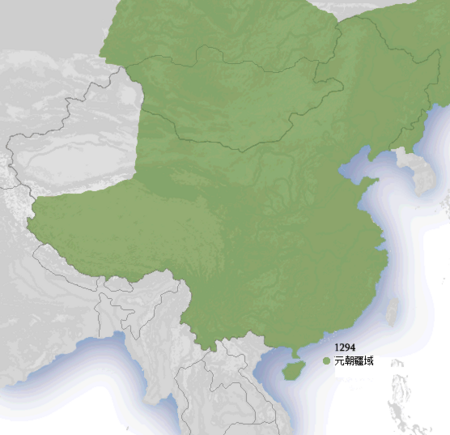
39°54′N 116°23′E / 39.900°N 116.383°E / 39.900; 116.383 مملكة يوان 大元 مملكة يوان الكبرى خاقان من الإمبراطورية المغوليةسلالة غازية في الصين 1271 – 1368 نفوذ سلالة يوان حوالي عام 1294غوريو كان أرضًا متنازع عليها[ا] ولايات يوان في 1330ولايات يوان في 1330 عاصمة خان بالق (بكين)...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Where Is Vidya BalanSutradaraSrinivas GuttulaProduserVenu Gopal Reddy[1]PemeranJyotii Sethi Prince CecilPenata musikKamran AhmedTanggal rilis 26 Juni 2015 (2015-06-26) NegaraIndiaBahasaTelugu Where is Vidya Balan adalah sebuah film ...

الصحراء الكبرى الموقع البلد عشرة دول: المغرب الجزائر تونس ليبيا مصر السودان موريتانيا مالي النيجر تشاد المساحة 9,400,000 كلم² الإحداثيات 23°05′N 12°37′E / 23.08°N 12.61°E / 23.08; 12.61 الارتفاعات القصوى 3,415 م إيمي كوسي الدنيا −133 م منخفض القطارة الحرا�...

Study of the history of the forms of words For other uses, see Etymology (disambiguation). Etymologies redirects here. For the work by Isidore of Seville, see Entymologiae. Not to be confused with Entomology or Etiology. Part of a series onLinguistics OutlineHistoryIndex General linguistics Diachronic Lexicography Morphology Phonology Pragmatics Semantics Syntax Syntax–semantics interface Typology Applied linguistics Acquisition Anthropological Applied Computational Conversation analysis Co...

American saxophonist and bandleader Kamasi WashingtonWashington in 2017Background informationBorn (1981-02-18) February 18, 1981 (age 43)Los Angeles, California, U.S.GenresJazzOccupation(s)MusicianInstrument(s)Tenor saxophoneYears active2000–presentLabelsYoungXLBrainfeederMember ofWest Coast Get DownWebsitekamasiwashington.comMusical artist Kamasi Washington (born February 18, 1981) is an American jazz saxophonist.[1] He is a founding member of the jazz collective West Coast Ge...

2003 studio album by John Hiatt & The GonersBeneath This Gruff ExteriorStudio album by John Hiatt & The GonersReleasedMay 6, 2003Recorded2002–03GenreRockLength50:00LabelNew West[1]ProducerDon Smith, John Hiatt, The GonersJohn Hiatt & The Goners chronology The Tiki Bar is Open(2001) Beneath This Gruff Exterior(2003) Master of Disaster(2005) Professional ratingsReview scoresSourceRatingAllMusic[2]The Guardian[3]Uncut[4] Beneath This Gruff E...





