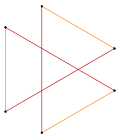
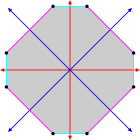
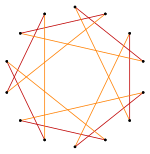
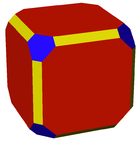
Изогональная фигура
| ||||||||||||||||||||||||||||||||||||||||
Read other articles:

Medan MarelanKecamatanPeta lokasi Kecamatan Medan MarelanMedan MarelanPeta lokasi Kecamatan Medan MarelanKoordinat: 3°42′21″N 98°39′33″E / 3.705703°N 98.659184°E / 3.705703; 98.659184Koordinat: 3°42′21″N 98°39′33″E / 3.705703°N 98.659184°E / 3.705703; 98.659184Negara IndonesiaProvinsiSumatera UtaraKotaMedanPemerintahan • CamatMuhammad Yunus, S.STP[1]Populasi (2021)[2] • To...

Multiuse venue in Swansea, Wales Swansea.com Stadium Stadium Swansea.comSwansea.com Stadium Stadium Swansea.comLocation within SwanseaFormer namesWhite Rock Stadium (2004, under construction)[1] New Stadium Swansea (2005, official)[2]Liberty Stadium (2005–2021)LocationNormandy Road,[3] Swansea, WalesCoordinates51°38′32″N 3°56′06″W / 51.6422°N 3.9351°W / 51.6422; -3.9351Public transitThe New Mex bus stop SwanseaOwnerCity and County ...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) لمعانٍ أخرى، طالع ساحة الحرية (توضيح). ساحة الحريةمعلومات عامةالعنوان حي العزيزية، حلب، سورياا�...

Men's Greco-Roman 75 kgat the Games of the XXXI OlympiadMedalistsVenueCarioca Arena 2Date14 August 2016Competitors20 from 20 nationsMedalists Roman Vlasov Russia Mark Madsen Denmark Kim Hyeon-woo South Korea Saeid Abdevali Iran← 20122020 → Wrestling at the2016 Summer OlympicsQualificationFreestyleGreco-RomanWomen57 kg59 kg48 kg65 kg66 kg53 kg74 kg75 kg58 kg86 kg85 kg63 kg97 kg98 kg69 kg125 kg130 kg75 kgvte Main article: Wrestling at the...

AwardNavy Occupation Service MedalObverseTypeService medalAwarded forOccupation duty during and/or following World War IIPresented byDepartment of the NavyEligibilityNavy, Marine Corps, and Coast Guard personnelClaspsEuropeAsiaStatusNo longer awardedEstablishedJanuary 22, 1947[1]First awardedMay 8, 1945Last awardedOctober 3, 1990Service ribbon and streamer PrecedenceNext (higher)World War II Victory MedalEquivalentArmy of Occupation MedalNext (lower)Medal for Humane Action T...

Titus O'NeilO'Neil di bulan April 2015Nama lahirThaddeus Michael BullardLahir29 April 1977 (umur 46)Boynton Beach, Florida,Amerika Serikat[1]Alma materUniversity of FloridaAnak2Karier gulat profesionalNama ringTitus O'Neil[2]Rufus PattersonTinggi6 ft 4 in (1,93 m)[2]Berat270 pon (120 kg)[2]Asal dariLive Oak, Florida[2]Tampa, Florida[3]Dilatih olehFlorida Championship WrestlingDebut2009[4] Thaddeus Michael Bu...

Restaurant in Paris, FranceCafé des 2 MoulinsRestaurant informationStreet address15, rue LepicCityParisPostal/ZIP Code75018CountryFranceCoordinates48°53′5.75″N 2°20′1″E / 48.8849306°N 2.33361°E / 48.8849306; 2.33361 Inside the Café The Café des 2 Moulins (French for Café of the Two Windmills) is a café in the Montmartre area of Paris, located at the junction of Rue Lepic and Rue Cauchois (the precise address is 15, rue Lepic, 75018 Paris). It takes its...

17th-century French dramatist (1639–1699) For other people named Jean Racine, see Jean Racine (disambiguation). Racine redirects here. For other uses, see Racine (disambiguation). This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (April 2016) (Learn how and when to remove this message) Jean RacinePortrait of RacineBornJean-Baptiste Racine(1639-12-21)21 Decembe...

Pour les articles homonymes, voir Piton (homonymie). Piton de la Fournaise Le sommet vu depuis le rebord du rempart de Bellecombe au sud-ouest. Géographie Altitude 2 632 m[1] Massif Massif du Piton de la Fournaise Coordonnées 21° 14′ 35″ sud, 55° 42′ 26″ est[1],[2] Administration Pays France Département et région d'outre-mer La Réunion Communes Sainte-Rose, Saint-Philippe Ascension Première 21 septembre 1751 par Andoche Dolnet de Palmar...

President of Peru from 2021 to 2022 For other people named Pedro Castillo, see Pedro Castillo (disambiguation). In this Spanish name, the first or paternal surname is Castillo and the second or maternal family name is Terrones. Pedro CastilloOSP OCACastillo in 202263rd President of PeruIn office28 July 2021 – 7 December 2022Prime MinisterGuido BellidoMirtha VásquezHéctor ValerAníbal TorresBetssy ChávezVice PresidentFirst Vice PresidentDina BoluarteSecond Vice PresidentV...

Uma resolução da Assembleia Geral das Nações unidas é uma decisão tomada pela Assembleia Geral das Nações Unidas sem força jurídica no direito internacional público, diferentemente das resoluções do Conselho de Segurança das Nações Unidas. Tal resolução é aceita se for votada pela maioria absoluta dos membros (a não ser algumas questões importantes que exigem uma maioria de dois terços). Seleção das resoluções Esta lista contém algumas resoluções consideradas...

Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. Будь ласка, допоможіть удосконалити цю статтю, додавши посилання на надійні (авторитетні) джерела. Зверніться на сторінку обговорення за поясненнями та допоможіть виправити недоліки. Мат...

Members of the New South Wales Legislative Assembly who served in the fourth parliament of New South Wales held their seats from 1860 to 1864:[1][2][3][4] The Speaker was Terence Murray until 13 October 1862 and then John Hay.[5] Name Electorate Years in office Alexander, MauriceMaurice Alexander [d] Goulburn 1861–1872 Allen, William BellWilliam Allen Williams 1860–1864 Arnold, William MunningsWilliam Arnold Paterson 1856–1875 Atkin...

Material fuelling nuclear reactors Fuel rod redirects here. Not to be confused with FuelRod. Nuclear fuel process A graph comparing nucleon number against binding energy Close-up of a replica of the core of the research reactor at the Institut Laue-Langevin Nuclear fuel is material used in nuclear power stations to produce heat to power turbines. Heat is created when nuclear fuel undergoes nuclear fission. Nuclear fuel has the highest energy density of all practical fuel sources. The processe...
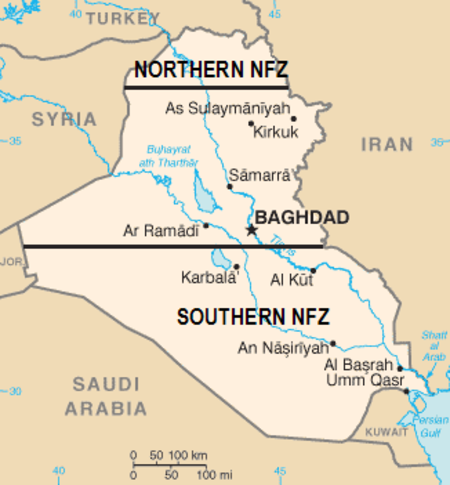
Militarily-enforced area prohibiting certain aircraft This article is about the military zone. For the civil regulatory use, see Prohibited airspace. For the football defensive backfield, see 2015 Denver Broncos season. Countries previously subject to no-fly zones – Iraq, Bosnia and Herzegovina, and Libya A no-fly zone, also known as a no-flight zone (NFZ), or air exclusion zone (AEZ),[1] is a territory or area established by a military power over which certain aircraft...

Pour les articles homonymes, voir onde (homonymie). Pour l'appareil électroménager utilisant cette technologie, voir Four à micro-ondes Expérience de transmission par micro-ondes (Laboratoire de la NASA). Spectre des rayonnements électromagnétiques en fonction de leur longueur d'onde. On retrouve notamment les micro-ondes, possédant une longueur d'onde entre 2 mm et 30 cm. Les micro-ondes ou microondes sont des rayonnements électromagnétiques[1] de longueur d'onde intermé...

كأس العالم لكرة القدم 2006 (بالإنجليزية: 2006 FIFA World Cup) الغلاف البريطاني للعبة فيفا كأس العالم المطور إي أيه كندا بلاي ستيشن بورتبل الناشر إي أيه سبورتس سلسلة اللعبة ألعاب فيديو كأس العالم لكرة القدم النظام جيم بوي أدفانس نينتندو جيم كيوب نينتندو دي إس إكس بوكس مايكروسوفت ...

1969-71 criminal prosecutions New Haven Black Panther trialsPart of Black Power movementCourtroom sketch of the murder trial in 1971.Date1970-71LocationNew Haven, ConnecticutCauseKidnapping and murder of Alex RackleyOutcomeReactions Popularization of trials Unrest in New Haven Popular distrust of the FBI Rulings Lonnie McLucas convicted of conspiracy to commit murder Warren Kimbro and George W. Sams Jr. convicted of murder Bobby Seale and Ericka Huggins: all charges dismissed after hung jury ...

Girolamo Maria GottiPrefek Kongrgeasi Penyebaran ImanGerejaGereja Katolik RomaPenunjukan29 Juli 1902Masa jabatan berakhir19 Maret 1916PendahuluMieczysław Halka-LedóchowskiPenerusDomenico SerafiniJabatan lainKardinal-Imam Santa Maria della Scala pro hac vice (1895–1916)ImamatTahbisan imam20 Desember 1856oleh Raffaele BialeTahbisan uskup27 Maret 1892oleh Lucido Maria ParocchiPelantikan kardinal29 November 1895oleh Paus Leo XIIIPeringkatKardinal-ImamInformasi pribadiNama lahirAnton...

Election in Taiwan This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: 2024 Taiwanese general election – news · newspapers · books · scholar · JSTOR (November 2023) 2024 Taiwanese general election ← 2020 13 January 2024 2028 → Presidential election← 20202028 →...