QR-алгоритм
|
Read other articles:
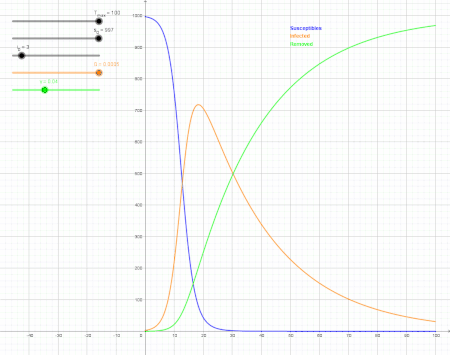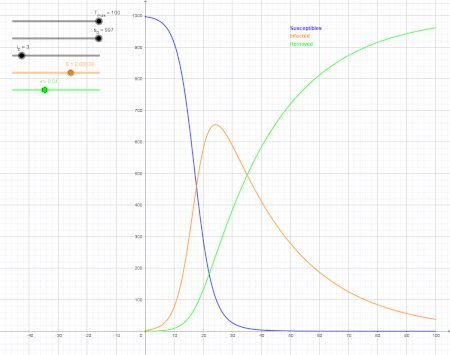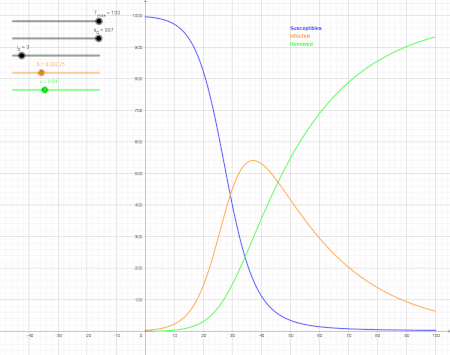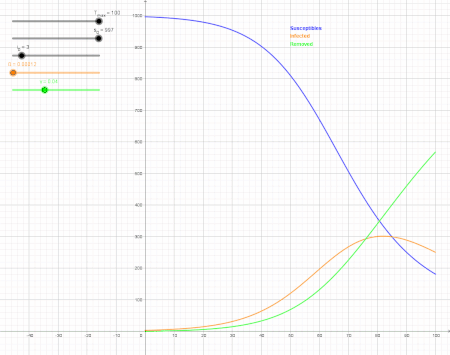
Measures such as social distancing and stay-at-home orders reduce and delay the peak of active cases, allowing more time for healthcare capacity to increase and better cope with patient load.[1] Time gained through thus flattening the curve can be used to raise the line of healthcare capacity to better meet surging demand.[2] SIR model showing the impact of reducing the infection rate (orange) by 76 % Meratakan kurva adalah strategi kesehatan masyarakat yang diperkenalkan...

Halaman ini berisi artikel tentang kelahiran pada manusia. Untuk kelahiran oada mamalia dan hewan lainnya, lihat Kelahiran. Kelahiran anakIbu dan bayi baru lahir diperlihatkan dengan tutupan vernixInformasi umumNama lainPersalinan, partus, parturisiSpesialisasiObstetri, kebidananTipePersalinan pervaginam, operasi sesar[1][2]PenyebabKehamilanKomplikasiObstructed labour, postpartum bleeding, eclampsia, postpartum infection, birth asphyxia, neonatal hypothermia[3][4&#...

Untuk FTV Drama, lihat Suara Hati Istri. Mega Series Suara Hati IstriGenre Drama Roman Ditulis olehTim Kreatif MKFSutradara Sam Sarumpaet Joe Sandjaya (Eps. 1) Pemeran Masayu Anastasia Temmy Rahadi Georgina Andrea Hans Christian Hosman Yati Surachman Raya Adena Ilyas Bachtiar Tasman Taher Ferdi Ali Penggubah lagu temaEndaLagu pembuka″Hati Yang Kau Sakiti″ — RossaLagu penutup″Hati Yang Kau Sakiti″ — RossaPenata musikIshvara GiovanniNegara asal IndonesiaBahasa asliBahasa ...

National library of the United Kingdom British LibraryBritish Library building at St Pancras from the piazza51°31′46″N 0°07′37″W / 51.52944°N 0.12694°W / 51.52944; -0.12694Location96 Euston RoadLondon, NW1 2DB, United KingdomTypeNational libraryEstablished1 July 1973 (50 years ago) (1 July 1973)Architect(s)Colin St John WilsonMary Jane LongBranches1 (Boston Spa, West Yorkshire)CollectionItems collectedBooks, journals, newspapers, magazines, sound a...

1856 Liverpool Town Council election ← 1855 November 1, 1856 (1856-11-01) 1857 → 16 seats were up for election: one seat for each of the 16 wards33 (incl. Aldermen) seats needed for a majority Elections to Liverpool Town Council were held on Monday 2 November 1856. One third of the council seats were up for election, the term of office of each councillor being three years. Eleven of the sixteen wards were uncontested. After the election, the composition o...

Association football club in Austria For a similar names team, see 1. Wiener Neustädter SC. Not to be confused with former Austrian football champions First Vienna FC. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 1. Wiener Neustädter SC 2008 – news · newspapers · books · scholar · JSTOR (June 2016)...

Mary Arthur McElroy Ibu Negara Amerika Serikat PendahuluLucretia GarfieldPenggantiEllen Lewis Herndon Arthur Informasi pribadiLahirMary Arthur(1841-07-05)5 Juli 1841Greenwich, New YorkMeninggal8 Januari 1917(1917-01-08) (umur 75)Suami/istriJohn McElroySunting kotak info • L • B Mary Arthur McElroy (5 Juli 1841 – 8 Januari 1917) adalah saudara dari Presiden Amerika Serikat ke-21, Chester A. Arthur. Ia adalah Ibu Negara Amerika Serikat dari tahun 1881 hingga t...

Jeff LynneOBELynne pada tahun 2014LahirJeffrey Lynne30 Desember 1947 (umur 76)Birmingham, InggrisPekerjaanMusisiPenyanyi-penulis musikproduser musikTahun aktif1963–sekarangAnak2Karier musikGenreRockpopDiskoFunkBlue-eyed soulNew WaveSymphonic RockInstrumenVokalgitarbasskeyboarddrumLabelUnited ArtistsJetHarvestEpicSony BMGRepriseFrontiersArtis terkaitElectric Light OrchestraThe MoveThe Idle RaceTraveling WilburysSitus webjefflynne.com Jeffrey Lynne OBE (born 30 December 1947) merup...

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: San Marino Calcio. San Marino CalcioStagione 2008-2009Sport calcio Squadra San Marino Allenatore Franco Varrella poi Mario Petrone poi Marco Tosi Presidente Daniele De Luigi Seconda Divisione16º posto nel girone B. Maggiori presenzeCampionato: Scotti (33) Miglio...

Stasiun Kereta Quzhou衢州站Stasiun Kereta Quzhou, 4 Januari 2019LokasiKecheng, Kota Quzhou, ZhejiangOperatorBiro Kereta ShanghaiInformasi lainStatusBeroperasiKode stasiun Kode TMIS: 32621[1] Kode Telegraf: QEH Kode Pinyin: QZH KlasifikasiStasiun kelas 2SejarahDibuka1932 dengan nama Stasiun Kereta Api Quxian 6 Januari 2017, renovasi terbaru rampungSunting kotak info • L • BBantuan penggunaan templat ini Stasiun Kereta Quzhou berada di Ruopeng, Kota Quzhou, Zhejiang, Ti...

4th ruling government of Albania Government of Durrës4th Government of AlbaniaDecember 1918‒January 1920Date formed25 December 1918 (1918-12-25)Date dissolved29 January 1920 (1920-01-29)People and organisationsPrinceWilhelm of Wied(de jure)Prime MinisterTurhan Pasha PërmetiNo. of ministers8HistoryPredecessorToptani GovernmentSuccessorDelvina Government The Government of Durrës (Albanian: Qeveria e Durrësit) was the 4th ruling government of Albania formed af...

Voce principale: Associazione Sportiva Dilettantistica Vastese Calcio 1902. Associazione Calcio Pro VastoStagione 1978-1979Sport calcio Squadra Pro Vasto Allenatore Gianfranco Zeli poi Enzo Gerardi Presidente Angelo Ciancaglini Serie C216º posto nel girone C. Retrocesso in Serie D. Maggiori presenzeCampionato: Cardascia, Ilari, Raimondi, Zambon (32) Miglior marcatoreCampionato: Turchetti (8) 1977-1978 1979-1980 Si invita a seguire il modello di voce Questa pagina raccoglie le informazi...

Extinct class of jawless fishes ThelodontiTemporal range: Sandbian[1]–Late Devonian,[2] 458–359 Ma PreꞒ Ꞓ O S D C P T J K Pg N Among the flat-bodied forms are Lanarkia (top left), provided with long, spine-shaped scales, and Loganellia (top right and middle). Other thelodonts, such as Furcacauda from the Devonian of Canada (bottom) are deep-bodied, with lateral gill openings and a very large, forked tail.[3] Scientific classification Domain: Eukaryota King...

Voce principale: Montegranaro Calcio Fermana Football Club. Montegranaro Calcio Fermana Football ClubStagione 2017-2018Sport calcio Squadra Fermana Allenatore Flavio Destro All. in seconda Vincenzo Rodia Presidente Umberto Simoni Serie C14° Coppa Italia Serie CFase a gironi StadioStadio Bruno Recchioni (8.850) Abbonati444 Maggior numero di spettatori3.283 vS Sambenedettese (20 settembre 2017) Minor numero di spettatori680 vs Ravenna (22 dicembre 2017) Media spettatori1.300 2016-2017 20...

Данио-рерио Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёрые рыбыИн�...

Voce principale: Associazione Calcio Cesena. Associazione Calcio CesenaStagione 1997-1998Sport calcio Squadra Cesena Allenatore Corrado Benedetti Presidente Edmeo Lugaresi Serie C11º posto Coppa ItaliaPrimo turno Coppa Italia Serie C2º posto Maggiori presenzeCampionato: Scalabrelli (34) Miglior marcatoreCampionato: Agostini (18) StadioStadio Dino Manuzzi 1996-1997 1998-1999 Si invita a seguire il modello di voce Questa pagina raccoglie le informazioni riguardanti l'Associazione Calcio...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

莎拉·阿什頓-西里洛2023年8月,阿什頓-西里洛穿著軍服出生 (1977-07-09) 1977年7月9日(46歲) 美國佛羅里達州国籍 美國别名莎拉·阿什頓(Sarah Ashton)莎拉·西里洛(Sarah Cirillo)金髮女郎(Blonde)职业記者、活動家、政治活動家和候選人、軍醫活跃时期2020年—雇主內華達州共和黨候選人(2020年)《Political.tips》(2020年—)《LGBTQ國度》(2022年3月—2022年10月)烏克蘭媒�...

إمارة سيلاند وهي عبارة عن دولة مجهرية تقع على ميناء قبالة ساحل المملكة المتحدة. الدولة المجهرية أوالدولة المصغرة (بالإنجليزية: Micronation) هي كيان يعبر عن دولة أو أمة، هذه الدولة لا تعترف بها حكومات الدول الأخرى أو المنظمات الدولية.[1][2][3] هذه الدول توجد فقط على الو...

Portuguese music genre This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Coimbra Fado – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) Fado group Rapsódia performing at Serenata Monumental (2010, Coimbra, Portugal) Coimbra Fado (Portuguese: Fado de Coimbra) is a genre of...






































