–І–Є—Б–ї–µ–љ–љ–Њ–µ —А–µ—И–µ–љ–Є–µ —Г—А–∞–≤–љ–µ–љ–Є–є
|
Read other articles:

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Hiu tidur pasifik Somniosus pacificus Status konservasiHampir terancamIUCN161403 TaksonomiKerajaanAnimaliaFilumChordataKelasChondrichthyesOrdoSqua...

ЎІўДЎѓўИЎ±ўК ЎІўДўДЎІЎ™ўБўК ЎІўДўЕўЕЎ™ЎІЎ≤ 2010 Ў™ўБЎІЎµўКўД ЎІўДўЕўИЎ≥ўЕ ЎІўДЎѓўИЎ±ўК ЎІўДўДЎІЎ™ўБўК ЎІўДўЕўЕЎ™ЎІЎ≤ ЎІўДўЖЎ≥ЎЃЎ© 20 ЎІўДЎ®ўДЎѓ ўДЎІЎ™ўБўКЎІ ЎІўДЎ™ЎІЎ±ўКЎЃ Ў®ЎѓЎІўКЎ©:9 Ў£Ў®Ў±ўКўД 2010 ўЖўЗЎІўКЎ©:13 ўЖўИўБўЕЎ®Ў± 2010 ЎІўДўЕўЖЎЄўЕ ЎІЎ™Ў≠ЎІЎѓ ўДЎІЎ™ўБўКЎІ ўДўГЎ±Ў© ЎІўДўВЎѓўЕ ЎІўДЎ®ЎЈўД ўЖЎІЎѓўК Ў≥ўГўИўЖЎ™ўИ ўЕЎ®ЎІЎ±ўКЎІЎ™ ўЕўДЎєўИЎ®Ў© 135 ЎєЎѓЎѓ ЎІўДўЕЎіЎІЎ±ўГўКўЖ 10 ЎІўДЎѓўИЎ±ўК ЎІўДўДЎІЎ™ўБўК ЎІўДўЕўЕЎ™ЎІЎ≤ 2009 ЎІ...

–Т –Т–Є–Ї–Є–њ–µ–і–Є–Є –µ—Б—В—М —Б—В–∞—В—М–Є –Њ –і—А—Г–≥–Є—Е –ї—О–і—П—Е —Б —Д–∞–Љ–Є–ї–Є–µ–є –Ъ–Њ—Б—В–∞–Ї–Є. –£ —Н—В–Њ–≥–Њ —В–µ—А–Љ–Є–љ–∞ —Б—Г—Й–µ—Б—В–≤—Г—О—В –Є –і—А—Г–≥–Є–µ –Ј–љ–∞—З–µ–љ–Є—П, —Б–Љ. –Т–µ–љ–Є–∞–Љ–Є–љ (–Ј–љ–∞—З–µ–љ–Є—П). –Т–µ–љ–Є–∞–Љ–Є–љ –Ъ–Њ—Б—В–∞–Ї–Є–Љ–Њ–ї–і. –Т–∞—Б–Є–ї–µ –Ъ–Њ—Б—В–∞–Ї–Є –У–Њ—Б–њ–Њ–і–∞—А—М –Ь–Њ–ї–і–∞–≤–Є–Є 1807 вАФ 26 –Є—О–ї—П 1812 –Я—А–µ–і—И–µ—Б—В–≤–µ–љ–љ–Є–Ї –Ь—Г—А—Г–Ј–Є, –Р–ї–µ–Ї—Б–∞–љ–і—А –Я—А–µ–µ–Љ–љ–Є–Ї –°–Ї–∞—А–ї–∞—В –Ъ–∞–ї–ї–Є–Љ–∞–Ї–Є –†–Њ–ґ–і–µ–љ–Є...

Rebecca RiggLahirRebecca Jane RiggTahun aktif1977 вАУ Sampai Sekarang Rebecca Jane Rigg atau lebih dikenal dengan nama Rebecca Rigg (31 Desember 1967) merupakan seorang aktris yang berasal dari Australia. Ia tampil diserial The Restless Year (1977) ketika itu umurnya baru 10 tahun. Namanya cukup populer ketika bermain difilm Fatty Finn (1980) yang juga merupakan film perdananya. Di Hollywood Rebecca Rigg terkenal lewat serial Michael Hayes (1997-1998). Filmografi The Restless Years (197...

Active stratovolcano on the east coast of Sicily, Italy Mongibello redirects here. For the fictional location, see Mongibello (The Talented Mr. Ripley). Mount EtnaEtna with the city of Catania in the foreground (December 2007)Highest pointElevation3,357 m (11,014 ft)(varies)[1][2]Prominence3,357 m (11,014 ft)Ranked 56thIsolation998.79 km (620.62 mi) ListingUltraCoordinates37¬∞45.3вА≤N 14¬∞59.7вА≤E / 37.7550¬∞N 14.9950¬∞E&...

International web registry for animal names The taxon treatment for the frog Paedophryne amauensis,[1] mentioning the LSID for this nomenclatural act.[2] ZooBank is an open access website intended to be the official International Commission on Zoological Nomenclature (ICZN) registry of zoological nomenclature.[3] Any nomenclatural acts (e.g. publications that create or change a taxonomic name) published electronically need to be registered with ZooBank prior to publica...

Qiu HuizuoйВ±дЉЪдљЬQiu Huizuo pada 1955 Direktur Departemen Logistik Umum TPRMasa jabatan14 Oktober 1959 вАУ 24 September 1971PendahuluHong XuezhiPenggantiZhang Zongxun Informasi pribadiLahir(1914-04-16)16 April 1914Xingguo, Jiangxi, TiongkokMeninggal18 Juli 2002(2002-07-18) (umur 88)Beijing, TiongkokKarier militerPihak TiongkokDinas/cabangTentara Pembebasan RakyatMasa dinas1929вАУ1971Pangkat Letnan JenderalSunting kotak info вАҐ L вАҐ B Dalam nama Tionghoa i...

Vaccine in development A Zika virus vaccine is designed to prevent the symptoms and complications of Zika virus infection in humans. As Zika virus infection of pregnant women may result in congenital defects in the newborn, the vaccine will attempt to protect against congenital Zika syndrome during the current or any future outbreak.[1] As of April 2019, no vaccines have been approved for clinical use, however a number of vaccines are currently in clinical trials.[2][3]...

Scandinavian dessert Tilsl√Єrte bondepiker / bondepige med sl√Єr√Дnglamat / Tilsl√Єrte bondepiker Bondepige med sl√ЄrTypeDessertPlace of originScandinaviaMain ingredientsMashed fruit (apples or plums), whipped cream, bread- or rusk crumbs Media: Tilsl√Єrte bondepiker / bondepige med sl√Єr Verschleiertes Bauernm√§dchen served in a glass bowl Tilsl√Єrte bondepiker (lit. veiled peasant girls. Known in Swedish as √§nglamat; Danish: bondepige med sl√Єr; Norwegian: tilsl√Єrte bondepiker; ...

2016еєізЊОеЬЛзЄљзµ±йБЄиИЙ ← 2012 2016еєі11жЬИ8жЧ• 2020 → 538еАЛйБЄиИЙдЇЇеЬШеЄ≠дљНзН≤еЛЭйЬА270з•®ж∞СжДПи™њжЯ•жКХз•®зОЗ55.7%[1][2] вЦ≤ 0.8 % иОЈжПРеРНдЇЇ еФРзіН¬ЈеЈЭжЩЃ еЄМжЛЙиОЙ¬ЈеЕЛжЮЧй†У жФњеЕЪ еЕ±еТМйї® ж∞СдЄїеЕЪ еЃґйДЙеЈЮ зіРзіДеЈЮ зіРзіДеЈЮ зЂЮйАЙжР≠ж°£ ињИеЕЛ¬Јељ≠жЦѓ иТВеІЖ¬ЈеЗ±жБ© йАЙдЄЊдЇЇз•® 304[3][4][и®ї 1] 227[5] иГЬеЗЇеЈЮ/зЬБ 30 + зЈђ-2 20 + DC ж∞СйБЄеЊЧз•® 62,984,828[6] 65,853,514[6]...

American inventor Hiram Percy MaximHiram Percy Maxim, c.1914Born(1869-09-02)September 2, 1869Brooklyn, New YorkDiedFebruary 17, 1936(1936-02-17) (aged 66)La Junta, ColoradoResting placeRose Hill CemeteryAlma materMassachusetts Institute of Technology (1886)OccupationInventorSpouseJosephine HamiltonChildrenHiram Hamilton Maxim Percy Maxim LeeParentHiram Stevens MaximRelativesHudson Maxim (uncle)Call signW1AW (most notable) Hiram Percy Maxim (September 2, 1869 – February 17, 193...
Henfenfeld. Henfenfeld adalah kota yang terletak di distrik N√Љrnberger Land di Bayern, Jerman. Kota Henfenfeld memiliki luas sebesar 6.64 km¬≤. Henfenfeld pada tahun 2006, memiliki penduduk sebanyak 1.857 jiwa. lbsKota dan kotamadya di N√Љrnberger Land Alfeld Altdorf bei N√Љrnberg Burgthann Engelthal Feucht Happurg Hartenstein Henfenfeld Hersbruck Kirchensittenbach Lauf an der Pegnitz Leinburg Neuhaus an der Pegnitz Neunkirchen am Sand Offenhausen Ottensoos Pommelsbrunn Reichenschwand R...

Not to be confused with Khari Boli. 28¬∞39вА≤32вА≥N 77¬∞13вА≤16вА≥E / 28.6588423¬∞N 77.2211152¬∞E / 28.6588423; 77.2211152 Neighborhood of Delhi in IndiaKhari BaoliNeighborhood of DelhiCountry IndiaStateDelhiLanguages вАҐ OfficialHindiTime zoneUTC+5:30 (IST) A shop selling Dates in Khari Baoli market Californian almonds being sold at Khari Baoli market in Old Delhi. Khari Baoli (Hindustani: [k ∞ aЋРriЋР baЋРwriЋР]) is a street in Delhi, India kn...

Scott Morrison ministerial positions controversy This article is part of a series aboutScott Morrison Early life and career Member for Cook (2007вАУ2024) Abbott government Abbott Ministry Turnbull government First Turnbull Ministry Second Turnbull Ministry 2018 Liberal Party leadership spills Prime Minister of Australia(International trips) First Ministry Second Ministry 2019вАУ20 Australian fires Sports rorts affair COVID-19 pandemic in Australia Brereton Report Parliament House sexual misco...

Deputy head of state and head of government of the Philippines For a list, see List of vice presidents of the Philippines. Vice President of of the Republic of the PhilippinesPangalawang Pangulo ng PilipinasVice presidential sealVice presidential flagIncumbentSara Dutertesince June 30, 2022Government of the PhilippinesOffice of the Vice PresidentStyle Madam Vice President(informal) The Honorable(formal) Her Excellency(diplomatic) StatusSecond highest executive branch officerMember ofCabi...

ЎІўДЎ™ўЗЎІЎ® ЎІўДЎіЎ±ЎІўКўКўЖ ўЕЎєўДўИўЕЎІЎ™ ЎєЎІўЕЎ© ЎІўДЎІЎЃЎ™ЎµЎІЎµ ЎЈЎ® ЎІўДЎ±ўИўЕЎІЎ™Ў≤ўЕ ЎІўДЎ•ЎѓЎІЎ±Ў© Ў≠ЎІўДЎІЎ™ ўЕЎіЎІЎ®ўЗЎ© ЎІўДЎ™ўЗЎІЎ® ЎІўДўЕўБЎІЎµўД Ў™ЎєЎѓўКўД ўЕЎµЎѓЎ±ўК - Ў™ЎєЎѓўКўД ЎІўДЎ™ўЗЎІЎ® ЎІўДЎіЎ±ЎІўКўКўЖ[1] Ў£ўИ ЎІўДЎ™ўЗЎІЎ® ЎІўДЎіЎ±ўКЎІўЖ[2][1] Ў£ўИ ЎІўДЎ™ўЗЎІЎ® ЎіЎ±ўКЎІўЖўК[1] (Ў®ЎІўДЎ•ўЖЎђўДўКЎ≤ўКЎ©: Arteritis)вАП ўЗўИ ЎІўДЎ™ўЗЎІЎ® ЎђЎѓЎ±ЎІўЖ ЎІўДЎіЎ±ЎІўКўКўЖЎМ[3] ўИЎІўДЎ∞ўК ЎєЎІЎѓЎ© ўЕЎІ ўКўГўИўЖ ўЖЎ™пњљ...
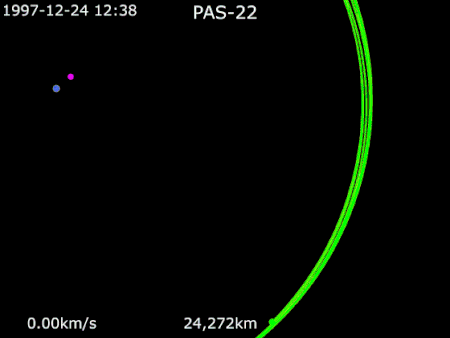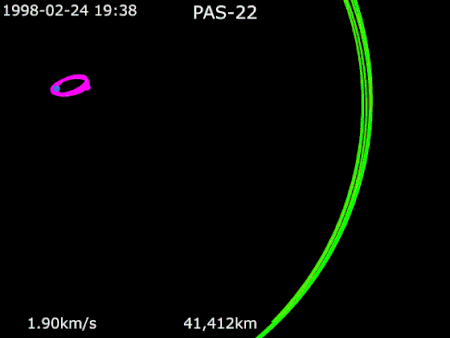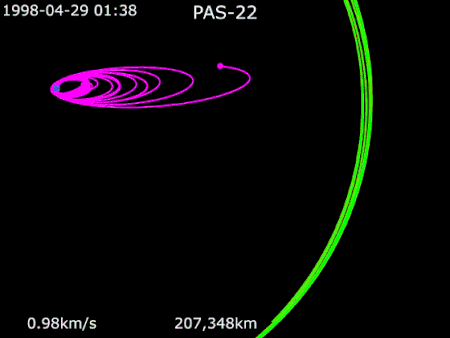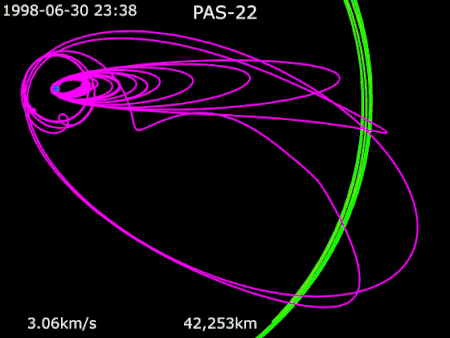
PanAmSat communications satellite AsiaSat 3 вЖТ HGS-1 вЖТ PAS-22NamesAsiaSat 3HGS-1PAS-22Mission typeCommunicationsOperatorAsiaSat (1997вАУ1998)Hughes (1998вАУ1999)PanAmSat (1999вАУ2002)COSPAR ID1997-086A SATCAT no.25126Mission duration15 years (planned) [1] 4 years (achieved) Spacecraft propertiesSpacecraftAsiaSat 3Spacecraft typeBoeing 601BusHS-601HPManufacturerHughes Space and CommunicationsLaunch mass3,465 kg[2]Dry mass2,500 kg (5,500 lb)Dimensions3.4 m x 3.5 m x...

Disambiguazione вАУ Sassari Torres rimanda qui. Se stai cercando la squadra di calcio femminile, vedi F.C. Sassari Torres Femminile. TorresCalcio Rossobl√є Segni distintiviUniformi di gara Casa Trasferta Terza divisa Colori sociali Rosso, blu SimboliTorre, Stemma comunale di Sassari InnoFozza TorresTrio Latte Dolce Dati societariCitt√†Sassari Nazione Italia ConfederazioneUEFA Federazione FIGC CampionatoSerie C Fondazione1903 Rifondazione1991Rifondazione2006Rifondazione2008Rifond...

Electronic device for selecting and compositing of live video sources Ross Video Vision 4 at Current TV Kahuna video switcher made by Snell Limited company presented at IBC 2010 A vision mixer is a device used to select between several different live video sources and, in some cases, compositing live video sources together to create visual effects. In most of the world, both the equipment and its operator are called a vision mixer or video mixer; however, in the United States, the equipment i...

For other uses, see Osmania. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Osmania General Hospital вАУ news ¬Ј newspapers ¬Ј books ¬Ј scholar ¬Ј JSTOR (October 2019) (Learn how and when to remove this message) Hospital in Telangana, IndiaOsmania General HospitalGovernment of TelanganaGeographyLocationHyderabad,...



![{\displaystyle [a,\;b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e682a8a7d3222e237401e57d673fd362523662cd)
![{\displaystyle \forall x\in [a,\;b]:\varphi (x)\in [a,\;b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7436b6a143e3b16d62d25665d34107045ef47077)
![{\displaystyle \exists \alpha <1:\forall x_{1},x_{2}\in [a,\;b]\quad ||\varphi (x_{1})-\varphi (x_{2})||\leq \alpha ||x_{1}-x_{2}||}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f115957ed12e317c5e5a99eb115bdd5fd68e56a0)






![{\displaystyle \varphi (x)\in C^{1}[a,\;b].\quad \forall x_{1},x_{2}\in (a,\;b),\quad x_{1}<x_{2}\quad \exists \xi \in (x_{1},\;x_{2}):\quad \varphi '(\xi )(x_{2}-x_{1})=\varphi (x_{2})-\varphi (x_{1})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4f22132153d13199f8d170e7d474962d1cd32df)

![{\displaystyle \forall x\in [a,\;b]\quad |\varphi '(x)|\leq 1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9588a85b37aa8d9097f47a2ed2ed7bdb4c9882e5)


















![{\textstyle {\vec {x}}^{[0]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97b764e2d4a7c7e067e3498b6c7ee91fd3543eda)
![{\displaystyle {\vec {x}}^{[j+1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/731295798153991209f20aaf78929acff1a3a6fa)
![{\displaystyle f_{i}+\sum _{k=1}^{n}{\frac {\partial f_{i}}{\partial x_{k}}}(x_{k}^{[j+1]}-x_{k}^{[j]})=0,\quad i=1,2,\ldots ,n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe9752ca6c08107f3914b5f1dfd1567dc69c34dc)
![{\displaystyle x^{[j]}=\left(x_{1}^{[j]}\ldots x_{k}^{[j]}\ldots x_{n}^{[j]}\right),\quad j=0,1,2,\ldots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/18e25b164e130f82edf7ba98ef315b5e16803fc9)