Транспозиционная матрица
|
Read other articles:

Contoh sebuah kolofon (cetakan tahun 1471) Kolofon dalam dunia percetakan atau pembuatan buku dapat berarti: Pemerian singkat mengenai catatan penerbitan atau produksi yang relevan dengan edisi tersebut. Dalam buku-buku modern biasanya ditempatkan pada bagian verso halaman judul, tetapi kadang kala juga ditempatkan di akhir buku, atau Tanda percetakan atau logotype Catatan produksi Pada buku-buku awal yang dicetak, kolofon, jika ada, merupakan pemerian singkat mengenai pencetakan dan penerbit...

American legislative district Map of Massachusetts House of Representatives' 4th Bristol district, based on the 2010 United States census. Massachusetts House of Representatives' 4th Bristol district in the United States is one of 160 legislative districts included in the lower house of the Massachusetts General Court. It covers part of Bristol County.[1] Republican Steven Howitt of Seekonk has represented the district since 2011.[2] Towns represented The district includes the...

Historical United States tariff In United States tax law history, the Tariff of 1883 (signed into law on March 3, 1883[1]), also known as the Mongrel Tariff Act by its critics, reduced high tariff rates only marginally, and left in place fairly strong protectionist barriers. President Chester A. Arthur appointed a commission in May 1882 to recommend how much tariff rates should be reduced. The issue was controversial during the last three decades of the nineteenth century, making tari...

Fanaticism towards a religion Religious fanaticism, or religious extremism, is a pejorative designation used to indicate uncritical zeal or obsessive enthusiasm that is related to one's own, or one's group's, devotion to a religion – a form of human fanaticism that could otherwise be expressed in one's other involvements and participation, including employment, role, and partisan affinities. Historically, the term was applied in Christian antiquity to denigrate non-Christian religions,...

Pour les articles homonymes, voir Ionesco. Eugène Ionesco Eugène Ionesco en 1993. Données clés Nom de naissance Eugen Ionescu Naissance 26 novembre 1909[1],[2] Slatina (Roumanie) Décès 28 mars 1994 (à 84 ans) Paris (France) Nationalité Roumaine Française Activité principale ÉcrivainDramaturgeProfesseur de lettres Auteur Langue d’écriture Francais Mouvement Théâtre de l'absurde Genres Théâtre Adjectifs dérivés « Ionescien » Œuvres principales La Cantatric...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

IljimaePoster promosi untuk IljimaeGenrePeriod drama, Action, RomanceBerdasarkanIljimaeoleh Ko Woo-youngDitulis olehChoi RanSutradaraLee Yong-sukPemeranLee Joon-giHan Hyo-jooLee Young-ahPark Si-hooNegara asalKorea SelatanBahasa asliBahasa KoreaJmlh. episode20ProduksiProduserLee Yong-sukLokasi produksiKoreaDurasiRabu dan Kamis pada pukul 21:55 (WSK)Rumah produksiChorokbaem MediaRilis asliJaringanSeoul Broadcasting SystemFormat gambar1080i (HDTV)Rilis21 Mei (2008-05-21) –24 Juli 20...

Voce principale: Football Club Treviso. Associazione Calcio TrevisoStagione 1982-1983Sport calcio Squadra Treviso Allenatore Vasco Tagliavini Presidente Alfonso Manzi Serie C110º posto nel girone A. Maggiori presenzeTotale: Santucci, Trevisan (34) Miglior marcatoreCampionato: Rondon (16) 1981-1982 1983-1984 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l'Associazione Calcio Treviso nelle competizioni ufficiali della stagione 1982-1983. Indice ...

Menteri Koperasi dan Usaha Kecil dan Menengah Republik IndonesiaPetahanaTeten Masdukisejak 23 Oktober 2019Dibentuk6 Juni 1968Pejabat pertamaM. Sarbini Berikut adalah daftar orang yang pernah menjabat sebagai Menteri Koperasi dan Usaha Kecil dan Menengah Republik Indonesia hingga saat ini. No Menteri Kabinet Mulai Menjabat Selesai Menjabat Keterangan Masih digabungkan dengan Menteri Transmigrasi Kerja I 10 Juli 1959 18 Februari 1960 [A] Kerja II 18 Februari 1960 6 Maret 1962 1 Ach...

Act of working together For other uses, see Collaboration (disambiguation). For the definition in music, between two or more artists, see Featuring. Catalan castellers collaborate, working together with a shared goal. Collaboration (from Latin com- with + laborare to labor, to work) is the process of two or more people, entities or organizations working together to complete a task or achieve a goal.[1] Collaboration is similar to cooperation. Most collaboration requires leadership, ...

Pemberontakan 1 Prairial Tahun IIIBagian dari Revolusi PrancisTanggal1 Prairial (20 Mei 1795)LokasiParis, Prancis Pemberontakan 1 Prairial Tahun III adalah sebuah pemberontakan populer di Paris pada 20 Mei 1795 terhadap kebijakan-kebijakan Konvensi Thermidorian. Peristiwa tersebut adalah salah satu pemberontakan populer dini dan paling diingat terakhir dari Revolusi Prancis.[1] Referensi ^ Rude 1967, hlm. 152. Sumber Lefebvre, Georges (1963). The French Revolution: from 1793 to 1...

National Rail station serving London Heathrow Airport Not to be confused with Heathrow Terminals 2 & 3 tube station. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Heathrow Terminals 2 & 3 railway station – news · newspapers · books · scholar · JSTOR (February 2021) (Learn how and when to remove thi...

1967 film by Gordon Douglas Tony RomeOriginal one-sheet posterDirected byGordon DouglasScreenplay byRichard L. BreenBased onMiami Mayhem1960 novelby Marvin AlbertProduced byAaron RosenbergStarringFrank SinatraJill St. JohnRichard ConteSue LyonCinematographyJoseph F. BirocEdited byRobert L. SimpsonMusic byLee Hazlewood (title song)Billy MayColor processDeLuxe ColorProductioncompanyArcola PicturesDistributed byTwentieth Century Fox Film CorporationRelease date November 10, 1967 (...

لمعانٍ أخرى، طالع جمال أباد (توضيح). جمال أباد تقسيم إداري البلد إيران إحداثيات 37°58′17″N 45°00′19″E / 37.97138889°N 45.00527778°E / 37.97138889; 45.00527778 تعديل مصدري - تعديل جمال أباد هي قرية آشورية مسيحية في مقاطعة أرومية، إيران. عدد سكان هذه القرية هو 209 في سنة 2006. ...

New York Red BullsJulukanNew York Red Bulls, Red Bulls, Metro, RBNYBerdiri1994; 30 tahun lalu (1994);[1] sebagaiNew York/New Jersey MetroStarsStadionRed Bull ArenaHarrison, NJ(Kapasitas: 25,189)Ketua Red Bull GmbHPelatih Kepala Gerhard StruberLigaMajor League Soccer2021Wilayah timur: ke-7Keseluruhan: ke-14Play-off: Babak pertamaSitus webSitus web resmi klub Kostum kandang Kostum tandang Musim ini New York Red Bulls merupakan sebuah tim sepak bola Amerika Serikat yang bermain...

Sports teams of a university Athletic teams representing California State University, Fullerton Cal State Fullerton TitansUniversityCalifornia State University, FullertonConferenceBig West Conference (primary)Mountain Pacific Sports Federation (swimming & diving)NCAADivision IAthletic directorJim DonovanLocationFullerton, CaliforniaVarsity teams6 men's & 8 women'sBasketball arenaTitan GymBaseball stadiumGoodwin FieldSoftball stadiumAnderson Family FieldSoccer stadiumTitan StadiumOther...

Formulas in differential geometry Binormal redirects here. For the category-theoretic meaning of this word, see normal morphism. A space curve; the vectors T, N and B; and the osculating plane spanned by T and N In differential geometry, the Frenet–Serret formulas describe the kinematic properties of a particle moving along a differentiable curve in three-dimensional Euclidean space R 3 {\displaystyle \mathbb {R} ^{3}} , or the geometric properties of the curve itself irrespective of any mo...

US indoor football league Continental Indoor Football LeagueMost recent season or competition:2014 Continental Indoor Football League seasonContinental Indoor Football League logoFormerlyOhio-Penn Indoor Football LeagueGreat Lakes Indoor Football LeagueSportIndoor footballFounded2005FounderEric SpitaleriJeff SpitaleriCory TrappFirst season2006Owner(s)Stuart SchweigertJim O'BrienRob LichtCountryUnited StatesMost recentchampion(s)Erie Explosion (2nd title)Most titlesCincinnati CommandosErie Exp...
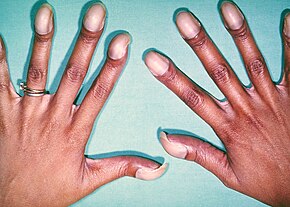
Type of congenital heart defect Not to be confused with Teratology. Medical conditionTetralogy of FallotOther namesFallot’s syndrome, Fallot’s tetrad, Steno-Fallot tetralogy[1]Diagram of a healthy heart and one with tetralogy of FallotSpecialtyCardiac surgery, pediatricsSymptomsEpisodes of bluish color to the skin, difficulty breathing, heart murmur, finger clubbing[2]ComplicationsIrregular heart rate, pulmonary regurgitation[3]Usual onsetFrom birth[4]Cause...

Dieser Artikel behandelt den US-amerikanischen Filmemacher James Benning; für den kanadischen Eishockeyspieler und -funktionär siehe Jim Benning. James Benning (Viennale 2012) James Benning (* 28. Dezember 1942 in Milwaukee, Wisconsin) ist ein US-amerikanischer Avantgarde-Filmemacher und Dokumentarfilmer. Inhaltsverzeichnis 1 Leben 2 Filmographie 3 Ausstellungen 4 Veröffentlichungen 5 Weblinks 6 Einzelnachweise Leben James Benning ist der Sohn deutscher Immigranten. Er studierte an der Un...

![{\displaystyle i,j\in [1,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e4a42afd86ce52621701173ebfde264b21e1bfd)














![{\displaystyle p,q,u,v\in [1,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2a1756fd43819cb74c82ba0faebdb4005b1921e)







![{\displaystyle R=[1,r_{2},...r_{n}]^{T},r_{2},...r_{n}\in [2,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e17b49a202dab40355db02fb9f71e3606500b0f2)








![{\displaystyle Trs(X).X=\parallel X\parallel ^{2}.[1,0,0,0]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f65b90778f8107abdc769c61f987da757ae76f5a)

