Кольцо частных
|
Read other articles:

River Where the Moon RisesPoster promosiNama alternatifMoon Rising RiverHangul달이 뜨는 강 GenreSejarahPembuatKBS Drama ProductionBerdasarkanPrincess Pyeonggangoleh Choi SagyuDitulis olehHan Ji-hoonKim Se-heeSutradaraYoon Sang-hoPemeranKim So-hyunNa In-wooLee Ji-hoonChoi Yu-hwaNegara asalKorea SelatanBahasa asliKoreaJmlh. episode20ProduksiProduser eksekutifYoon Jae-hyuk (KBS)ProduserJo Yoon-jungPengaturan kameraKamera tunggalRumah produksiVictory ContentsDistributorKBSViu OriginalRilis ...

Principality of Asturias Principado de Asturias (Spanyol)Principáu d'Asturies Wilayah OtohomComunidad Autónoma del Principado de Asturias BenderaLambang kebesaranMap of AsturiasCountry SpainCapitalOviedoPemerintahan • PresidentFrancisco Álvarez-Cascos Fernández (FAC)Luas(2.1% of Spain; Ranked 10th) • Total10.604 km2 (4,094 sq mi)Populasi (2006) • Total1.076.896 • Kepadatan100/km2 (260/sq mi) • Pop. rank13...

German multinational e-commerce company Look Again redirects here. For the 2010 novel, see Lisa Scottoline. Otto GmbH & Co KGFormerlyWerner Otto VersandhandelOtto VersandCompany typePrivateIndustryretail, e-commerceGenreMail orderFounded17 August 1949FounderWerner OttoHeadquartersHamburg, GermanyArea servedEurope, United States of America, Canada, AsiaKey peopleMichael Otto (Chairman of the Supervisory Board)Alexander Birken (CEO and Chairman of the Executive Board)[1]Revenue€16...

Head of Kenyan State Law Office Politics of Kenya National Government Constitution History Human rights LGBT rights Executive President (list) William Ruto Deputy President Rigathi Gachagua Cabinet Prime Cabinet Secretary Musalia Mudavadi Attorney General Justin Muturi Director of Public Prosecutions Renson M. Ingonga Legislature National Assembly Speaker: Moses Wetangula List of members Constituencies Senate Speaker: Amason Kingi List of members Judiciary Chief Justice Martha Koome Deputy Ch...

Facsimile of a Qing dynasty block printed Jigu Suanjing Jigu suanjing (Chinese: 緝古算經, Continuation of Ancient Mathematics) was the work of early Tang dynasty calendarist and mathematician Wang Xiaotong, written some time before the year 626, when he presented his work to the Emperor. Jigu Suanjing was included as one of the requisite texts for Imperial examination; the amount of time required for the study of Jigu Suanjing was three years, the same as for The Nine Chapters on the ...

Издательство политической литературы ЦК КПСС (Политиздат) Основано 1918 Ликвидировано 1991 Страна СССР Адрес 125811, Москва, Миусская площадь, 7[1] Код Госкомиздата СССР 079 Награды Информация в Викиданных ? Изда́тельство полити́ческой литерату́ры ЦК КПСС (Политизда́т) ...

Голубянки Самец голубянки икар Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ПервичноротыеБез ранга:ЛиняющиеБез ранга:PanarthropodaТип:ЧленистоногиеПодтип:ТрахейнодышащиеНадкласс:ШестиногиеКласс...

密西西比州 哥伦布城市綽號:Possum Town哥伦布位于密西西比州的位置坐标:33°30′06″N 88°24′54″W / 33.501666666667°N 88.415°W / 33.501666666667; -88.415国家 美國州密西西比州县朗兹县始建于1821年政府 • 市长罗伯特·史密斯 (民主党)面积 • 总计22.3 平方英里(57.8 平方公里) • 陸地21.4 平方英里(55.5 平方公里) • ...

Eurovision Song Contest 2022Country AzerbaijanNational selectionSelection processInternal selectionSelection date(s)Artist: 16 February 2022Song: 21 March 2022Selected entrantNadir RustamliSelected songFade to BlackSelected songwriter(s)Andreas Stone JohanssonAnderz WrethovSebastian SchubThomas StengaardFinals performanceSemi-final resultQualified (10th, 96 points)Final result16th, 106 pointsAzerbaijan in the Eurovision Song Contest ◄2021 • 2022 �...

Zlatko Junuzović Informasi pribadiTanggal lahir 26 September 1987 (umur 36)Tempat lahir Loznica, SFR YugoslaviaTinggi 1,71 m (5 ft 7+1⁄2 in)Posisi bermain GelandangInformasi klubKlub saat ini SV Werder BremenNomor 16Karier junior1994–1999 Kühnsdorf1999–2005 Grazer AKKarier senior*Tahun Tim Tampil (Gol)2005–2007 Grazer AK 70 (9)2007–2009 Austria Kärnten 57 (3)2009–2012 Austria Wien 82 (21)2012– SV Werder Bremen 109 (15)Tim nasional‡ Austria U-19 2 (1...

River Taff water bus service in Wales This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Cardiff Waterbus – news · newspapers · books · scholar · JSTOR (July 2018) (Learn how and when to remove this message) Cardiff WaterbusLocaleCardiff Bay and Cardiff City CentreWaterwayRiver TaffTransit typeWater busOperator...
بليزانتون الإحداثيات 28°58′01″N 98°29′06″W / 28.9669°N 98.485°W / 28.9669; -98.485 [1] تاريخ التأسيس 1858 تقسيم إداري البلد الولايات المتحدة[2][3] التقسيم الأعلى مقاطعة أتاسكوسا خصائص جغرافية المساحة 22.118291 كيلومتر مربع20.27997 كيلومتر مربع (1 أبري�...

Mona RudaoMona Rudao (tengah) dan para tetua suku lainnyaLahir(1880-05-21)21 Mei 1880FormosaMeninggal28 November 1930(1930-11-28) (umur 50)Prefektur Taichū, Taiwan JepangKebangsaanSeediqPekerjaanKepala desa MaheboAnak3Orang tuaLuhe Rudao Patung Mona Rudao di Taman Peringatan Peristiwa Wushe Mona Rudao atau Mouna Rudao (1880–1930; Hanzi: 莫那·魯道) adalah putra seorang kepala suku Seediq di Taiwan. Ia menggantikan ayahnya sebagai kepala desa Mahebo (Hanzi: 馬赫坡社) d...
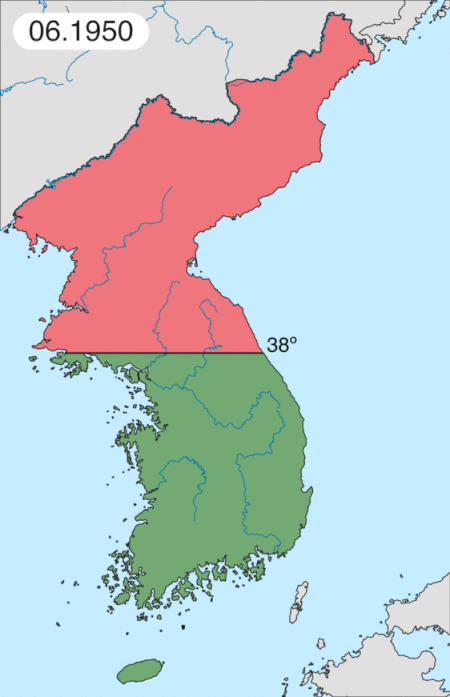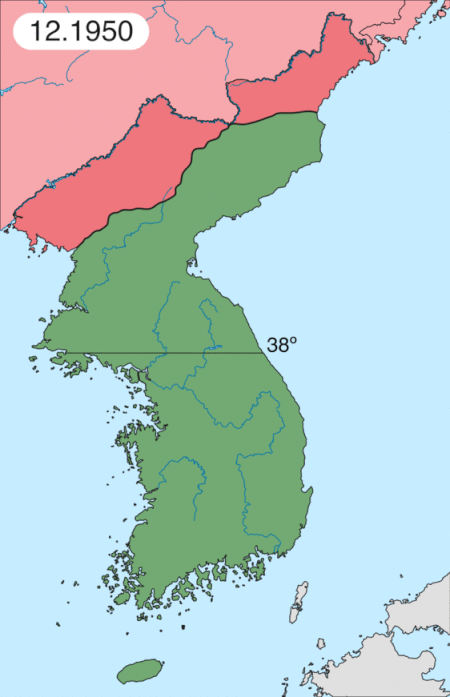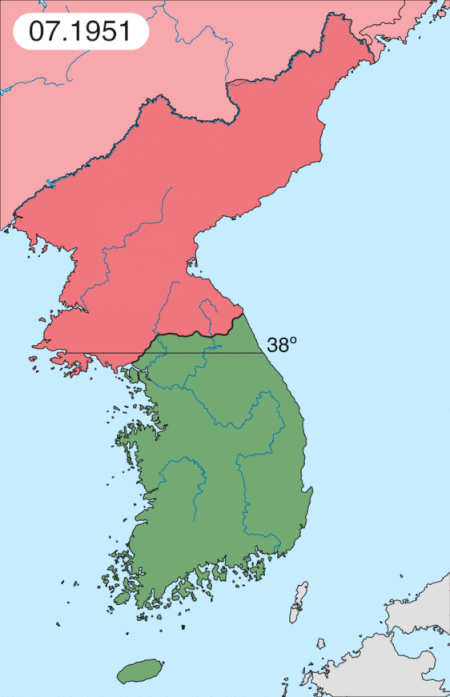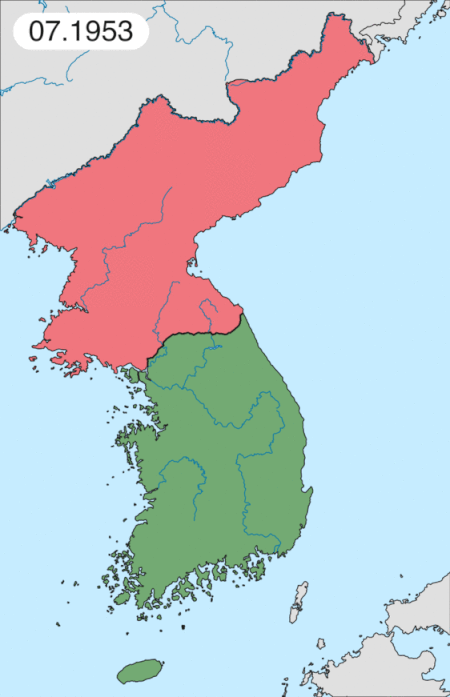
Korean War battle Battle of the Samichon RiverPart of the Korean WarChinese dead on the approaches to the Hook, late July 1953Date24−26 July 1953LocationJamestown Line, Samichon River, Korea38°1′44″N 126°50′13″E / 38.02889°N 126.83694°E / 38.02889; 126.83694Result United Nations victoryBelligerents United Nations (UNC) Australia New Zealand United States United Kingdom ChinaCommanders and leaders John Wilton Glenn C. Fu...
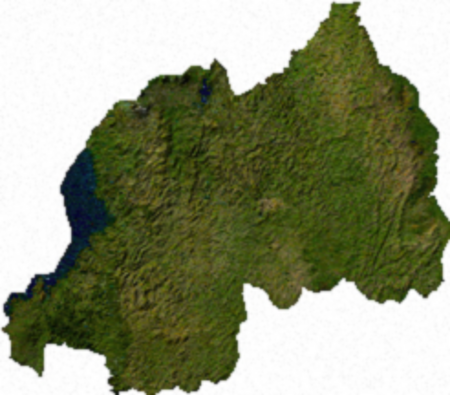
Geography of RwandaContinentAfrica[1]RegionEast AfricaCoordinates2°00′S 30°0′E / 2.000°S 30.000°E / -2.000; 30.000AreaRanked 144th • Total26,338 km2 (10,169 sq mi) • Land97% • Water3%Coastline0 km (0 mi)Borders893 km (DRC 217 km, Burundi 290 km, Tanzania 217 km, Uganda 169 km)Highest pointMount Karisimbi 4507 mLowest pointRusizi River 950 mLongest riverNyabarongoLargest lakeLake Kivu Satellit...

لمعانٍ أخرى، طالع مندل (توضيح). غريغور يوهان مندل (بالألمانية: Gregor Mendel)[1] معلومات شخصية اسم الولادة (بالألمانية: Johann Mendel) الميلاد 20 يوليو 1822 [2][3] الوفاة 6 يناير 1884 (61 سنة) [1][4][5][6][7][8] برنو[1][8] سبب الوفاة ...

Communication with a deity or other supernatural entity This article is about supernatural revelation. For the final book of the New Testament, see Book of Revelation. For other uses, see Revelation (disambiguation). This article has an unclear citation style. The references used may be made clearer with a different or consistent style of citation and footnoting. (April 2011) (Learn how and when to remove this message) Illumination from Liber Scivias, showing Hildegard of Bingen receiving a v...

This article is about the chemical element. For other uses, see Tin (disambiguation). Stannum redirects here. For other uses, see Stannum (disambiguation). For the chemical compound with formula TiN, see Titanium nitride. Chemical element with atomic number 50 (Sn)Tin, 50SnTinAllotropessilvery-white, β (beta); gray, α (alpha)Standard atomic weight Ar°(Sn)118.710±0.007[1]118.71±0.01 (abridged)[2] Tin in the periodic table Hydrogen Helium Lithium Beryllium Bor...

Location where the Proto-Uralic language originated Current distribution of the Uralic languages The Proto-Uralic homeland is the earliest location in which the Proto-Uralic language was spoken, before its speakers dispersed geographically causing it to diverge into multiple languages. Various locations have been proposed and debated, although as of 2022 scholarly consensus now gravitates towards a relatively recent provenance of the Uralic languages east of the Ural mountains.[1] Hom...

Language family of West Africa MandeEthnicityMandé peoplesGeographicdistributionWest AfricaLinguistic classificationNiger–Congo?MandeProto-languageProto-MandeSubdivisions Western Mande Eastern Mande Language codesISO 639-5dmnLinguasphere00- (phylozone)Glottologmand1469 The Mande languages (Mandén, Manding; [needs IPA]) are a group of languages spoken in several countries in West Africa by the Mandé peoples. They include Maninka (Malinke), Mandinka, Soninke, Bambara, Kpelle, Jula ...











![{\displaystyle k[X_{1},X_{2},...,X_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba7aa81a9f758a101152377a3825e85e50f82145)









