Гильбертово пространство
|
Read other articles:

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (نوفمبر 2019) بطولة الأمم الرئيسية 1909 تفاصيل الموسم بطولة الأمم الستة النسخة 27 التاريخ بداية:16 يناير 1909 نهاي�...
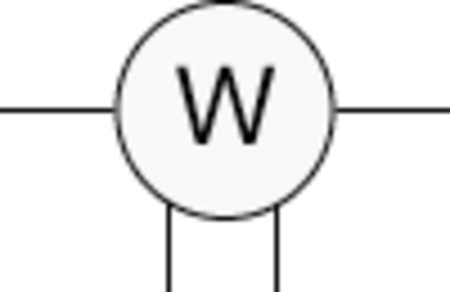
Le wattmètre est un appareil qui mesure la puissance électrique consommée par un récepteur ou fournie par un générateur électrique. La puissance s'exprime en watts et ses multiples comme le kilowatt et ne doit pas être confondue avec l'énergie qui s'exprime en joules ou en kilowatts-heures. Wattmètre Représentation symbolique d'un wattmètre dans un circuit. Principe Le wattmètre monophasé est muni d’un capteur de courant (ampèremètre), d’un capteur de tension (voltmètre) ...

German kingdom formed from the Electorate of Saxony (1806–1918) This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Kingdom of Saxony – news · newspapers · books · scholar · JSTOR (March 2017) (Learn how and when to remove this template message) Kingdom of SaxonyKönigreich Sachsen (German)1806–1918 Top: Flag of Saxony (1815-1918) Bottom: Flag of S...

Statewide coal strike in Colorado during 1927–1928 1927-1928 Colorado Coal StrikePart of the Coal WarsDateOctober 18, 1927 - May, 1928LocationColoradoResulted inUnion victory, $1/day wage increaseParties Industrial Workers of the World Colorado Fuel & Iron Co. Rocky Mountain Fuel Co. Colorado Rangers Police[1] Knights of Columbus Ku Klux Klan Lead figures Kristin Svanum A. S. Embree Adam Bell; Amelia Milka Sablich Jesse F. Welborn; Louis Scherf Casualties and losses Deaths: 8 ki...

Pangkalan TNI AU MuljonoLambang LanudNegara IndonesiaCabang TNI Angkatan UdaraTipe unitPangkalan Udara MiliterBagian dariKomando Operasi Udara IIMotoPrayatna Kerta GeganaSitus webhttp://lanud-muljono.tni-au.mil.id/ Pangkalan TNI AU Muljono adalah satuan pelaksana Komando Operasi Udara II yang berkedudukan langsung di bawah Pangkoopsud II yang terletak di Surabaya, Provinsi Jawa Timur.[1] Pangkalan TNI AU Surabaya bertugas menyiapkan dan melaksanakan pembinaan dan pengoperasian seluruh...

Voce principale: Siracusa Calcio. Siracusa CalcioStagione 1978-1979Sport calcio Squadra Siracusa Allenatore Carlo Facchin Presidente Claudio Cassone Serie C2 - Gir. D2º posto (promosso in Serie C1) Coppa Italia SemiproVincitore Maggiori presenzeCampionato: Favero (33) Miglior marcatoreCampionato: Ballarin (17) 1977-1978 1979-1980 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti il Siracusa Calcio nelle competizioni ufficiali della stagione 1978-1...

Finnish footballer (born 1984) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (September 2017) (Learn how and when to remove this template message) Antti Hynynen Personal informationDate of birth (1984-05-30) 30 May 1984 (age 39)Place of birth Tampere, Finland[1]Height 1.80 m (5 ft 11 in)Position(s) Midfielder, DefenderTeam informa...

In trigonometria, le formule di prostaferesi permettono di trasformare somme e differenze di funzioni trigonometriche di due angoli in un prodotto di funzioni trigonometriche. La parola prostaferesi deriva dalla giustapposizione di due parole greche, prosthesis (πρόσθεσις) e aphairesis (ἀφαίρεσις), che significano rispettivamente somma e sottrazione. Le formule di prostaferesi furono definite, nella forma attualmente nota, da Johann Werner agli inizi del XVI secolo, tuttavi...

American YouTuber and political commentator For the American football player, see Blair White. Blaire WhiteWhite in 2019Personal informationBorn (1993-09-14) September 14, 1993 (age 30)Corning, California, U.S.EducationCalifornia State University, ChicoOccupation(s)YouTuber and political commentatorYouTube informationChannels Blaire White The Blaire White Project Years active2015–presentGenre(s)Politics, vlogSubscribers1.4 million (Blaire White)612,000 (The Blaire White Project)&#...

City in Oklahoma, United StatesEdmond, OklahomaCity FlagSealWordmarkMotto: A Great Place To GrowLocation in Oklahoma County and the state of Oklahoma.Coordinates: 35°39′N 97°28′W / 35.650°N 97.467°W / 35.650; -97.467CountryUnited StatesStateOklahomaCountyOklahomaFoundedApril 22, 1889[1]Government • TypeCouncil – Manager • MayorDarrell Davis[2] • City managerScot Rigby[3]Area[4] •...

Type of stellar remnant composed mostly of electron-degenerate matter Degenerate dwarf redirects here. Not to be confused with Degenerate star. For other uses, see White dwarf (disambiguation). Image of Sirius A and Sirius B taken by the Hubble Space Telescope. Sirius B, which is a white dwarf, can be seen as a faint point of light to the lower left of the much brighter Sirius A. A white dwarf is a stellar core remnant composed mostly of electron-degenerate matter. A white...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

Cet article est une ébauche concernant un aéronef, le domaine militaire et la Russie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Kronstadt Orion Kronstadt Orion des forces aériennes de la fédération de Russie Constructeur Kronstadt group Rôle drone de combat Mise en service 2020 Date de retrait Toujours en service Équipage 0 Dimensions Envergure 16 m Longueur 8 m Hauteur 2 m Masses À ...

Strada statale 148PontinaLocalizzazioneStato Italia Regioni Lazio Province Roma Latina DatiClassificazioneStrada statale InizioRoma FineTerracina Lunghezza109,200[1] km Data apertura1950 Provvedimento di istituzioneD.P.R. 28 giugno 1950, n. 650[2] GestoreANAS Manuale La strada statale Pontina (SS 148)[3], in precedenza strada regionale 148 Pontina (SR 148)[4], è una strada statale che collega Roma a Terracina (LT), passando per Latina e per...

Kabel jenis twisted-pair untuk 10BaseT Plug 8P8C (bukan RJ-45) pada 10BaseT 10BaseT adalah sebuah standar yang digunakan untuk mengimplementasikan jaringan berbasis teknologi Eternet. Dibandingkan dengan standar 10Base2 atau 10Base5, standar 10BaseT ini lebih populer, meski kecepatan yang ditawarkan adalah sama, yaitu 10 Megabit per detik. 10BaseT menggunakan kabel Unshielded Twisted-Pair (UTP) untuk menghubungkan komputer, dan menggunakan hub untuk membentuk sebuah jaringan. 10BaseT mendukun...

Institutional corruption in the country A map depicting Corruption Perceptions Index in the world in 2022; a higher score indicates lower levels of corruption 100 – 90 89 – 80 79 – 70 69 – 60 59 – 50 49 – 40 39 – 30 29 – 20 19 – 10 9 – 0 No data Political corruption Forms and concepts Bribery Cronyism Economics of corruption Electoral fraud El...

U.S. Army staff position responsible for investigations of Army personnel Provost Marshal of the United States ArmyArmy Staff Identification BadgeIncumbentMG Duane R. Millersince August 5, 2021[1]Department of the ArmyReports toChief of Staff of the ArmyFormationJanuary 10, 1776First holderCPT William MaronyWebsiteOfficial Website The provost (pronounced provo) marshal general is a United States Army staff position that handles investigations of U.S. Army personnel. It is the hig...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sukadana – news · newspapers · books · scholar · JSTOR (May 2011) (Learn how and when to remove this message) Town in West Kalimantan, IndonesiaSukadanaTownLiong Chinese dragon dance on the street of SukadanaCoordinates: 1°15′0″S 109°57′0″E / ...

1985 world's fair held in Ibaraki, Japan Expo 85 redirects here. For the other expo in 1985, see Expo 85 (Plovdiv, Bulgaria). Tsukuba Expo '85Fuyō PavilionOverviewBIE-classSpecialized expositionCategoryInternational specialized expositionNameTsukuba Expo '85MottoDwellings and surroundings – Science and Technology for Man at HomeArea102 hectares (250 acres)Visitors20,334,727MascotCosmo HoshimaruParticipant(s)Countries111Organizations3Business18LocationCountryJapanCityTsukuba Science CityTim...

Branch of philosophy Checker shadow illusion Do we see what is really there? The two areas of the image marked A and B, and the rectangle connecting them, are all of the same shade: our eyes automatically correct for the shadow of the cylinder. The philosophy of perception is concerned with the nature of perceptual experience and the status of perceptual data, in particular how they relate to beliefs about, or knowledge of, the world.[1] Any explicit account of perception requires a c...



































































![{\displaystyle L^{2}[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fe6267bd20634cf723a413e92533ca417ce3319)
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



