Integral de Riemann
|
Read other articles:

Achmad Diran Wakil Gubernur Kalimantan Tengah ke-7Masa jabatan4 Agustus 2005 – 4 Agustus 2015PresidenSusilo Bambang Yudhoyono Joko WidodoGubernurAgustin Teras Narang PenggantiSaid IsmailBupati Barito Selatan ke-7Masa jabatan1996–2001 PendahuluAsmawi AganiPenggantiBaharuddin H. Lisa Informasi pribadiLahir1 Januari 1949 (umur 75)Surakarta, Jawa Tengah, IndonesiaKebangsaanIndonesiaPartai politikPANAnakTomy Irawan DiranAlma materUniversitas Lambung Mangkurat, Banjarmasin...

Cet article est une ébauche concernant une chanson ukrainienne. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Pour les articles homonymes, voir 1944. 1944 Jamala pendant une des répétitions de sa chanson 1944 Single de Jamalaextrait de l'album 1944 Sortie 2015 Durée 3:00 Langue Anglais, Tatar de Crimée[1] Genre Ethnique Auteur Susana Jamaladinova Label Enjoy Chansons représentant l'Ukraine au Concou...

زين الدين زيدان Zinédine Zidane زيدان في عام 2017 معلومات شخصية الاسم الكامل زين الدين يزيد زيدان[1] الميلاد 23 يونيو 1972 (العمر 51 سنة)[2]مارسيليا، فرنسا الطول 1.85 م (6 قدم 1 بوصة)[3] مركز اللعب وسط مهاجم الإقامة مدريد، إسبانيا الجنسية فرنسي[أ] الديانة الإسلام[6]...

Questa voce sull'argomento politici italiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Sandro Parcaroli Sindaco di MacerataIn caricaInizio mandato24 settembre 2020 PredecessoreRomano Carancini Presidente della Provincia di MacerataIn caricaInizio mandato19 dicembre 2021 PredecessoreAntonio Pettinari Dati generaliPartito politicoLega per Salvini Premier Titolo di studioDip...

International organization BSEC redirects here. For other uses, see BSEC (disambiguation). Organization of the Black Sea Economic CooperationFormation25 June 1992TypeEconomic cooperation organizationHeadquartersIstanbul, TurkeyLocationEastern EuropeSoutheastern EuropeWestern AsiaMembership 13 member countries Albania Armenia Azerbaijan Bulgaria Georgia Greece Moldova North Macedonia Romania Russia Serbia Turkey Ukra...

Questa voce sull'argomento allenatori di calcio francesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Sébastien Desabre Desabre nel 2018 Nazionalità Francia Calcio Ruolo Allenatore Squadra RD del Congo Carriera Carriera da allenatore 2004-2006 ESC Rocheville(vice)2006-2010 ESC Rocheville2010-2012 ASEC Mimosas2012-2013 Cotonsport Garoua2013-2014 EspéranceInterim2014 Espé...

University and Further Education College in Birmingham, England University College BirminghamMottoService Before SelfTypePublicEstablished1957PrincipalMichael HarkinStudents4,930 HE (2019/20)[1]Undergraduates4,435 (2019/20)[1]Postgraduates495 (2019/20)[1]Other students10,335 FE[2]LocationBirmingham, United KingdomWebsiteucb.ac.ukUniversity College Birmingham is a university in Birmingham, England. It was awarded full university status in 2012 along with Newman ...

Type of sports venue This article is about the sports venue. For other uses, see Tennis court (disambiguation). Indoor tennis courts at the University of Bath, England A tennis court is the venue where the sport of tennis is played. It is a firm rectangular surface with a low net stretched across the centre. The same surface can be used to play both doubles and singles matches. A variety of surfaces can be used to create a tennis court, each with its own characteristics which affect the playi...

Kurds in FinlandTotal population16,603 (0.3%)Regions with significant populationsUusimaa8,573 (0.5%)[1]Southwest Finland2,861 (0.6%)[1]Pirkanmaa871 (0.2%)[1]Päijät-Häme809 (0.4%)[1]Central Finland487 (0.2%)[1]LanguagesFinnish and KurdishReligionSunni Islam Christianity Atheism YazidismRelated ethnic groupsIranian peoples Part of a series on: Kurdish history and Kurdish culture People List of Kurds Population Homeland Kurdistan Turkey (Northern...

Former province of Sicily, Italy Place in Sicilia, ItalyProvince of PalermoProvince(1860–2015) FlagCoat of armsMap highlighting the location of the province of Palermo in ItalyCountry ItalyRegionSiciliaCapital(s)PalermoComuni82Area • Total4,992 km2 (1,927 sq mi)Population (2012) • Total1,249,533 • Density250/km2 (650/sq mi)Time zoneUTC+1 (CET) • Summer (DST)UTC+2 (CEST)Postal code90010, 90010-90035, 90037-90049, 9...

Province of Turkey This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Çorum Province – news · newspapers · books · scholar · JSTOR (October 2023) (Learn how and when to remove this message) Province in TurkeyÇorum ProvinceProvinceLion Gate in HattusaLocation of the province within TurkeyCountryTurkeySeatÇoru...

Sceaux 行政国 フランス地域圏 (Région) イル=ド=フランス地域圏県 (département) オー=ド=セーヌ県郡 (arrondissement) アントニー郡小郡 (canton) 小郡庁所在地INSEEコード 92071郵便番号 92330市長(任期) フィリップ・ローラン(2008年-2014年)自治体間連合 (fr) メトロポール・デュ・グラン・パリ人口動態人口 19,679人(2007年)人口密度 5466人/km2住民の呼称 Scéens地理座標 北緯48度4...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

Cục Tác chiến Điện tửHoạt động30/4/1992 (32 năm, 15 ngày)Quốc gia Việt NamPhục vụ Quân đội nhân dân Việt NamPhân loạiCục chuyên ngành (Nhóm 3)Chức năngLà cơ quan quản lý tác chiến điện tử đầu ngànhQuy mô20.000 ngườiBộ phận củaBộ Tổng Tham mưuBộ chỉ huyHà NộiCác tư lệnhCục trưởngTrung tướng Nguyễn Long Biên Cục Tác chiến Điện tử [1][2] trực thu�...

Street in Buenos Aires, Argentina Night shot of Figueroa Alcorta Avenue with the UBA Faculty of Law to the right The avenue on its route towards the Barrio Parque area. Avenida Figueroa Alcorta is a major thoroughfare in Buenos Aires, Argentina, with a length of over 7 km (4.3 mi) along the city's northside. History The rapid northward growth of the city of Buenos Aires during the late nineteenth century was facilitated by plans for a number of boulevards in the area by Mayor Torcua...

Extinct order of tetrapodomorphs SeymouriamorphaTemporal range: Late Carboniferous[1] - Late Permian Fossil of Seymouria in the National Museum of Natural History Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Clade: Reptiliomorpha (?) Order: †SeymouriamorphaWatson, 1917 Subgroups See text. Seymouriamorpha were a small but widespread group of limbed vertebrates (tetrapods). They have long been considered stem-amniotes (reptiliomorphs), and most p...

A catena is a sequence of soils down a slope, created by the balance of processes such as precipitation, infiltration and runoff. A catena in soil science (pedology) is a series of distinct but co-evolving soils arrayed down a slope.[1] Each soil type or facet differs somewhat from its neighbours, but all occur in the same climate and on the same underlying parent material. A mature catena is in equilibrium as the processes of deposition and erosion are in balance. Concept The term so...

Барвінкове Герб Барвінкового Прапор Барвінкового Краєвид на засніжене Барвінкове з щогли ретранслятора в сутінки (наприкінці листопада) Основні дані Країна Україна Область Харківська область Район Ізюмський район Громада Барвінківська міська громада Код КАТОТТГ:...

City in Ohio, United StatesSalem, OhioCitySalem Downtown Historic District FlagSealLocation of Salem in Columbiana County and in the State of OhioSalemShow map of OhioSalemShow map of the United StatesCoordinates: 40°54′34″N 80°51′55″W / 40.90944°N 80.86528°W / 40.90944; -80.86528CountryUnited StatesStateOhioCountiesColumbiana, Mahoning[1]Founded1806Named forSalem, New JerseyGovernment • TypeStatutoryArea[2] • Total6...

Angiografi substraksi digitalIntervensiContoh pemberian bahan kontras iodin pada angiografi serebral.MeSHD015901[sunting di Wikidata] Angiografi substraksi digital adalah pemeriksaan yang memberikan gambaran permukaan bagian dalam pembuluh darah, termasuk arteri, vena, dan serambi jantung. Gambaran ini diperoleh dengan menggunakan mesin sinar-X terkomputerisasi yang kompleks. Media kontras khusus disuntikkan agar pasokan darah ke kaki, jantung atau organ tubuh lainnya dapat di lihat denga...
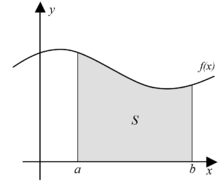

![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)







![{\displaystyle [x_{i},x_{i+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7138606cdb8eb7dddaba59b5aefe1ade6bc05a1b)






























