Primitiva
|
Read other articles:
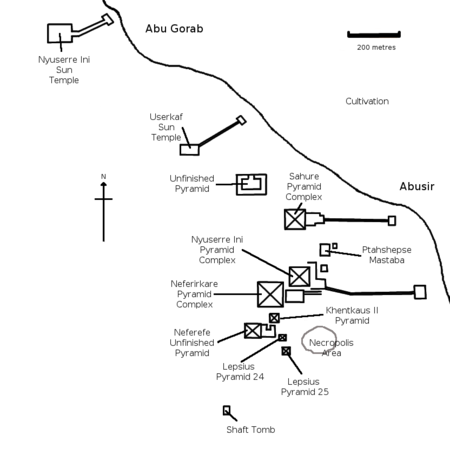
Denah situs Abusir Busiri Era: Kerajaan Baru(1550–1069 BC) Hieroglif Mesir Abusir (Arab: ابو صير pelafalan dalam bahasa Egyptian Arabic: [æbuˈsˤiːɾ]; Bahasa Mesir pr wsjr; bahasa Koptik: ⲃⲟⲩⲥⲓⲣⲓ busiri, Rumah atau Kuil Osiris; bahasa Yunani Kuno: Βούσιρις) adalah situs arkeologi yang terletak dua puluh lima kilometer barat daya Kairo, yang dikenal dengan piramida beberapa firaun dari Dinasti ke-V[1][2] Situs ini...

Pour les articles homonymes, voir Guerre sociale. Guerre sociale (Rome) Le Sabinium. La confédération des Marses, forte de 100 000 hommes et dirigée par Pompédius Silo, provenait de la zone au sud-est de cette carte, située sous le lac Fucinus ; elle coalisait d'autres peuples. Informations générales Date 91 à 88 av. J.-C. Lieu Italie Issue Victoire militaire romaine Changements territoriaux Aucun Belligérants République romaine Groupe marsien : Marses (Italie)P...

Trans-Iranian RailwayTrans-Iranian railway in the Veresk BridgeIkhtisarNama asliراهآهن سراسری ایرانTerminusBandar-e EmamGorganOperasiDibuka1927Perpanjangan terakhir1963Diselesaikan1938Data teknisLebar sepur1.435 mm (4 ft 8+1⁄2 in) sepur standar Jalur kereta api Trans-Iran pada tahun 1938. Jalur kereta api Trans-Iran ( Persia : راه آهن سراسری ایران) adalah proyek pembangunan jalur kereta api utama yang dimulai pada tahun 1927 ...

Slovak professional tennis player Karol BeckCountry (sports) SlovakiaResidenceZvolen, SlovakiaBorn (1982-04-03) 3 April 1982 (age 41)Zvolen, CzechoslovakiaHeight1.80 m (5 ft 11 in)Turned pro2001Retired2018 (last match in 2020)PlaysRight-handed (two-handed backhand)Prize money$2,110,846SinglesCareer record65–116Career titles0Highest rankingNo. 36 (22 August 2005)Grand Slam singles resultsAustralian Open3R (2005)French Open1R (2003, ...

History of the Focke-Wulf Fw 190 Main article: Focke-Wulf Fw 190 An Fw 190 A-8/R2 in American hands The Focke-Wulf Fw 190 Würger was used by the Luftwaffe during the Second World War in a variety of roles. Like the Messerschmitt Bf 109, the Fw 190 was employed as a workhorse, and proved suitable for a wide variety of roles, including air superiority fighter, strike fighter, ground-attack aircraft, escort fighter, and operated with less success as a night fighter. It served on ...

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Associazione Sportiva Pro Gorizia. Associazione Sportiva Pro GoriziaStagione 1946-1947Sport calcio Squadra Pro Gorizia Allenatore Giacomo Blason Presidente Aldo Paoli Tacchini Serie B20º posto nel girone B. Retrocessa in Serie C. Ripescata per motivi politici. M...

Love O2OPosterNama lainTionghoa微微一笑很倾城 SutradaraZhao TianyuProduserZhang YibaiDitulis olehGu ManBerdasarkanJust One Smile Is Very Alluring by Gu ManPemeranyang yang zheng shuangPenata musikNathan WangPerusahaanproduksiShanghai GCod Entertainment Huace Pictures (Tianjing) Tianjin Lianrui Pictures Dongyang Yixing Media Shanghai Tencent Pictures Taiyang Chuanghe Media[1]DistributorHuace Pictures (Tianjing) Tianjin Lianrui Pictures Shanghai Tencent Pictures[1...

Process that involves reducing the amount of waste produced in society waste prevention redirects here. For the prevention of uncontrolled waste dumping, see Pollution. Waste hierarchy. Refusing, reducing, reusing, recycling and composting allow to reduce waste. Waste minimisation is a set of processes and practices intended to reduce the amount of waste produced. By reducing or eliminating the generation of harmful and persistent wastes, waste minimisation supports efforts to promote a more ...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may be very hard to understand. Please help clarify it. (January 2020) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Kadambathur – news · newspaper...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

تاي مو شان الموقع منتصف الأقاليم الجديدة، هونغ كونغ المنطقة هونغ كونغ إحداثيات 22°24′42″N 114°07′23″E / 22.4118°N 114.123°E / 22.4118; 114.123 الارتفاع 957 متر (3,140 قدم) تعديل مصدري - تعديل تاي مو شان (بالصينية: 大帽山، وتعني جبل القبعة الكبيرة) هو أعلى جبل في منطقة هونغ كو�...

يعكس مصطلح حساب رأس المال أو الحساب التمويلي ضمن الاقتصاد الكلي والتمويل الدولي صافي التغير في حقوق الملكية للموجودات الوطنية.[1][2][3] وهو أحد جزئين رئيسيين من ميزان المدفوعات حيث أن الجزء الثاني هو الحساب الجاري الذي يعكس صافي الدخل القومي. الفائض في حساب رأس ا...

Culturally recognised union between people For other uses, see Marriage (disambiguation), Matrimony (disambiguation), and Wedlock (disambiguation). Married and Matrimony redirect here. For other uses, see Married (disambiguation) and Matrimony (disambiguation). Part of a series on theAnthropology of kinship Basic concepts Family Lineage Affinity Consanguinity Marriage Incest taboo Endogamy Exogamy Moiety Monogamy Polygyny Polygamy Concubinage Polyandry Bride price Bride service Dowry Parallel...

Queen of Denmark from 1972 to 2024 For other people with the same name, see Margaret of Denmark (disambiguation). Margrethe IIMargrethe II in 2012Queen of DenmarkReign14 January 1972 – 14 January 2024PredecessorFrederik IXSuccessorFrederik XBorn (1940-04-16) 16 April 1940 (age 84)Amalienborg, Copenhagen, DenmarkSpouse Henri de Laborde de Monpezat (m. 1967; died 2018)IssueDetail Frederik X Prince Joachim NamesMargrethe Alexandrine Þó...

Valley in Poland and the Czech Republic Location of Kłodzko Valley Central Sudetes Eastern Sudetes Kłodzko Valley in the geomorphological system of the Czech Republic Kłodzko Valley The Kłodzko Valley (Polish: Kotlina Kłodzka, Czech: Kladská kotlina, German: Glatzer Kessel) a valley in the Sudetes mountain range, that covers the central part of Kłodzko County in south-western Poland, with the southern tip extending to the Czech Republic around the town of Král�...

Magical Circle Guru Guru魔法陣グルグル(Mahōjin Guru Guru)GenrePetualangan, Komedi, Fantasi, Percintaan MangaPengarangHiroyuki EtōPenerbitEnixMajalahMonthly Shōnen GanganDemografiShōnenTerbit1992 – 2003Volume16 Seri animeSutradaraNobuaki NakanishiSkenarioChika HojoChinatsu HoujouHideki MitsuiMayumi KoyamaYasuhiro KomatsuzakiStudioNippon AnimationSaluranasliTV AsahiTayang 13 Oktober 1994 – 14 September 1995Episode45 Film animeSutradaraNobuaki NakanishiSkenarioHideki MitsuiStudioN...

Begonia hirsuta TaksonomiSuperkerajaanEukaryotaKerajaanPlantaeDivisiTracheophytaOrdoCucurbitalesFamiliBegoniaceaeGenusBegoniaSpesiesBegonia hirsuta Aubl., 1775 Begonia hirsuta adalah spesies tumbuhan yang tergolong ke dalam famili Begoniaceae. Spesies ini juga merupakan bagian dari ordo Cucurbitales. Nama ilmiah spesies ini pertama kali diterbitkan oleh Jean Baptiste Christophore Fusée Aublet pada 1775. Referensi Pranala luar Begonia hirsuta pada situs web The Plant List. Pengidentifikasi ta...

CGTN العربيةCGTN bahasa ArabDiluncurkan25 Juli 2009PemilikChina Global Television NetworkNegara Republik Rakyat TiongkokBahasaBahasa ArabKantor pusatBeijing, Republik Rakyat TiongkokSitus webCGTN العربيةTelevisi InternetCGTNCGTN العربية CGTN bahasa Arab (Hanzi: 中国环球电视网阿拉伯语频道; Bahasa Arab: سي جي تي إن العربية; sering disingkat sebagai CGTN العربية) adalah saluran berbahasa Arab yang terfokus pada jaringan televisi, CGTN d...

Sandor Wekerle (Porträt von Gyula Benczúr, 1911) Sándor Wekerle [ˈʃaːndor ˈvɛkɛrlɛ] (deutsch auch Alexander Wekerle; * 14. November 1848 in Mór, Königreich Ungarn; † 16. August 1921 in Budapest) war ein ungarischer Politiker und der erste nichtadelige Ministerpräsident seines Landes. Seine erste Amtszeit dauerte von 1892 bis 1895, die zweite von 1906 bis 1910. 1917 wurde er noch einmal für ein Jahr Ministerpräsident, er verlor das Amt im Herbst 1918 im Zuge der Asternrevoluti...

American political party United States Pirate Party CaptainDrew Bingaman (PA)FoundedJune 6, 2006; 18 years ago (2006-06-06)Youth wingYoung Pirates USAIdeologyPirate politicsCivil libertarianismDirect democracyPan-Americanism[1]Police reform[1]Political positionSyncreticInternational affiliationPirate Parties InternationalColorsPurple, Red, BlueSeats in the Senate0 / 100 Seats in the House0 / 435 Governorships0 / 50 State Upper Houses0 / 1,921 State Lower...





























































