Fundamentos da matemática
|
Read other articles:

Acestrorhynchus pantaneiro Status konservasiRisiko rendahIUCN186654 TaksonomiKerajaanAnimaliaFilumChordataKelasActinopteriOrdoCharaciformesFamiliAcestrorhynchidaeGenusAcestrorhynchusSpesiesAcestrorhynchus pantaneiro Naércio Aquino de Menezes, 1992 lbs Acestrorhynchus pantaneiro, yang lebih dikenal sebagai pike characin,[1] adalah sebuah spesies ikan dalam keluarga Acestrorhynchidae.[2] Spesies tersebut dideskripsikan oleh Naércio Aquino de Menezes pada 1992. Spesies tersebut...

هيد أف هاربور الإحداثيات 40°53′54″N 73°09′44″W / 40.898333333333°N 73.162222222222°W / 40.898333333333; -73.162222222222 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى سميثتاون خصائص جغرافية المساحة 7.9 كيلومتر مربع7.861613 كيلومتر مربع (1 أبريل 2010) ارتفاع 3...

Kepengarangan kitab-kitab dalam Alkitab masih terus dipelajari dan diperdebatkan. Beberapa kitab dalam Alkitab dianggap oleh para sarjana sebagai produk dari satu individu, dan semua telah diedit untuk menghasilkan karya-karya yang dikenal saat ini.[1] Berikut adalah kesimpulan dari mayoritas sarjana kontemporer, bersama dengan pandangan tradisional, baik Yahudi dan Kristen. Penulis ilahi Para Bapa Gereja awal setuju bahwa kitab suci itu terinspirasi atau didiktekan oleh Allah, tapi t...

Maket Rumah Ba'anjung Atap Ambin Sayup-Muka Ba'atap Balai Laki yang biasanya berdenah huruf T atau tanda + (tipe yang konsekuen berdenah + disebut Rumah Cacak Burung. Rumah Cacak Burung (gambar kiri) dan Rumah Palimbangan (gambar kanan). Rumah Ba'anjung Cacak Burung adalah salah satu jenis rumah Baanjung yaitu rumah tradisional suku Banjar (disebut rumah Banjar) di Kalimantan Selatan yang merupakan rumah hunian rakyat biasa yang umumnya para petani dan pekerja.[1] Rumah induk yang mem...

BarakacityHistoireFondation 9 janvier 2010Dissolution 28 octobre 2020CadreZone d'activité Monde entierType Organisation non gouvernementale internationaleForme juridique Association déclaréeDomaines d'activité Aide humanitaire, autres organisations fonctionnant par adhésion volontaireSiège Évry-CourcouronnesPays FranceOrganisationFondateur Idriss Sihamedi (d)Président Idriss Sihamedi (d) (depuis 2010)Site web barakacity.comIdentifiantsRNA W952001402SIREN 788779023modifier - modi...

Belut lintah Pacific hagfish beristirahat di dasar laut, pada kedalaman 280 m lepas pantai Oregon Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Subfilum: Vertebrata Superkelas: Cyclostomata Kelas: Myxini Ordo: Myxiniformes Famili: MyxinidaeRafinesque, 1815 Genera Rubicundinae Fernholm et al. 2013 Rubicundus Fernholm et al. 2013 Eptatretinae Bonaparte 1850 Eptatretus Cloquet 1819 Myxininae Nelson 1976 Myxine Linnaeus 1758 Nemamyxine Richardson 1958 Neomyxine Richardson 1953 Notom...

Núcleo Bandeiranteregione amministrativa LocalizzazioneStato Brasile Stato federato Distretto Federale MesoregioneNon presente MicroregioneNon presente TerritorioCoordinate15°52′12″S 47°58′04″W / 15.87°S 47.967778°W-15.87; -47.967778 (Núcleo Bandeirante)Coordinate: 15°52′12″S 47°58′04″W / 15.87°S 47.967778°W-15.87; -47.967778 (Núcleo Bandeirante) Superficie80,43 km² Abitanti36 472 Densità453,46 ab./km² Altre inf...

Huruf KirilI dengan aksen rendah Alfabet KirilHuruf SlaviaАА́А̀А̂А̄ӒБВГҐДЂЃЕЕ́ÈЕ̂ЁЄЖЗЗ́ЅИИ́ЍИ̂ЙІЇЈКЛЉМНЊОŌПРСС́ТЋЌУУ́ У̀У̂ӮЎФХЦЧЏШЩЪЫЬЭЮЯHuruf non-SlaviaӐА̊А̃Ӓ̄ӔӘӘ́Ә̃ӚВ̌ҒГ̑Г̣Г̌ҔӺҒ̌ӶД̌Д̣Д̆ӖЕ̄Е̃Ё̄Є̈ӁҖӜҘӞЗ̌З̱З̣ԐԐ̈ӠӢИ̃ҊӤҚӃҠҞҜК̣ԚӅԮԒӍӉҢԨӇҤО́О̀О̆О̂О̃ӦӦ̄ӨӨ̄Ө́Ө̆ӪҨԤР̌ҎҪС̣С̱Т̌Т̣ҬУ̃Ӱ Ӱ́Ӱ̄ӲҮҮ́ҰХ̣Х̱...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Hot in ClevelandImmagine dalla sigla della serieTitolo originaleHot in Cleveland PaeseStati Uniti d'America Anno2010-2015 Formatoserie TV Generesitcom Stagioni6 Episodi128 Durata22 min (episodio)45 min (finale di serie) Lingua originaleinglese Rapporto16:9 CreditiIdeatoreSuzanne Martin Interpreti e personaggi Valerie Bertinelli: Melanie Hope Moretti Jane Leeves: Rejoyla Joy Scroggs Wendie Malick: Victoria Chase Betty White: Elka Ostrovsky Doppiatori e personaggi Antonella Baldini: Melanie Hop...

SannakjiNama KoreaHangul산낙지 Alih AksarasannakjiMcCune–Reischauersannakchi Sannakji atau sannakji hoe merupakan makanan asal Korea yang terbuat dari gurita yang masih hidup yang dibumbui dengan wijen dan minyak wijen. Ada beberapa restoran yang menyajikan Sannakji hanya dengan meletakkannya di piring dengan sisa-sisa air garam dan melengkapinya dengan saus terpisah. Ada pula yang menyajikannya di atas sayuran rebus di dalam panci. Referensi http://www.sayangi.com/gayahidup1/kuliner/rea...

Béthemont-la-Forêt La fontaine-abreuvoir et le lave-sabots. Blason Administration Pays France Région Île-de-France Département Val-d'Oise Arrondissement Pontoise Intercommunalité CC de la Vallée de l'Oise et des Trois Forêts Maire Mandat Didier Dagonet 2020-2026 Code postal 95840 Code commune 95061 Démographie Gentilé Béthemontois Populationmunicipale 418 hab. (2021 ) Densité 110 hab./km2 Géographie Coordonnées 49° 03′ 00″ nord, 2° 15′ ...

American religious scholar (born 1942) The ReverendJ. Gordon MeltonBornJohn Gordon Melton (1942-09-19) September 19, 1942 (age 81)Birmingham, Alabama, U.S.Academic backgroundAlma materBirmingham Southern College, Garrett-Evangelical Theological Seminary, Northwestern UniversityAcademic workDisciplineMethodist, Religion, New religious movements, American religious historyInstitutionsBaylor UniversityNotable worksThe Encyclopedia of American Religions John Gordon Melton (born September 19,...

التهاب الشرايين معلومات عامة الاختصاص طب الروماتزم الإدارة حالات مشابهة التهاب المفاصل تعديل مصدري - تعديل التهاب الشرايين[1] أو التهاب الشريان[2][1] أو التهاب شرياني[1] (بالإنجليزية: Arteritis) هو التهاب جدران الشرايين،[3] والذي عادة ما يكون نت�...

Lake in Sussex County, New JerseyCulver's LakeCulver's Lake in Frankford Township, New Jersey.Culver's LakeShow map of New JerseyCulver's LakeShow map of the United StatesLocationFrankford Township, Sussex County, New JerseyCoordinates41°10′12″N 74°46′34″W / 41.170°N 74.776°W / 41.170; -74.776TypelakeSurface area555 acres (225 ha)Max. depth50 feet (15 m)Shore length16.5 miles (10.5 km)Surface elevation830 feet (250 m)1 Shore length is n...

Mathematical function relating circular and hyperbolic functions The Gudermannian function relates the area of a circular sector to the area of a hyperbolic sector, via a common stereographic projection. If twice the area of the blue hyperbolic sector is ψ, then twice the area of the red circular sector is ϕ = gd ψ. Twice the area of the purple triangle is the stereographic projection s = tan 1/2ϕ = tanh 1/2ψ. The blue point has coordinates (cosh ψ, sinh ψ). The red point has coordinat...
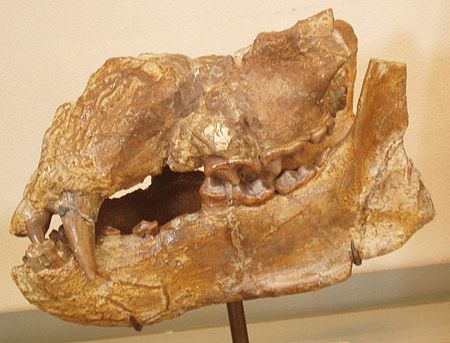
Family of carnivoran mammals Bear cub redirects here. For the 2004 film, see Bear Cub. This article is about the carnivoran mammals. For other uses, see Bear (disambiguation). BearsTemporal range: 38–0 Ma PreꞒ Ꞓ O S D C P T J K Pg N Late Eocene – Recent Brown bear (Ursus arctos) Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Carnivora Superfamily: Ursoidea Family: UrsidaeG. Fischer de Waldheim, 1817 Type genus UrsusLinnaeus, ...

Funerary inscription (AD 525) calling the deceased Maxima an Ancilla Christi (handmaid of Christ) In the Catholic Church, Servant of God is the style used for a person who has been posthumously declared heroic in virtue during the investigation and process leading to canonisation as a saint.[1] The term is used in the first of the four steps in the canonization process. The next step is being declared Venerable, upon a decree of heroism or martyrdom by the honored. That is followed b...

How to Handle WomenKartu lobiSutradaraWilliam James CraftProduserCarl LaemmleDitulis oleh Carl Krusada (skenario) Jack Foley (adaptasi) Albert DeMond (titel) CeritaWilliam James CraftJack FoleyPemeran Glenn Tryon Marian Nixon SinematograferArthur L. ToddPenyuntingCharles CraftDistributorUniversal PicturesTanggal rilis 14 Oktober 1928 (1928-10-14) Durasi60 menitNegaraAmerika SerikatBahasaBisu (intertitel Inggris) How to Handle Women adalah sebuah film komedi bisu Amerika Serikat tahun 192...

千葉県を流れる利根川水系の河川については「黒部川 (千葉県)」をご覧ください。 黒部川 黒部川河口から朝日、白馬~五竜岳、立山連峰水系 一級水系 黒部川種別 一級河川延長 85 km平均流量 12.18 m3/s(宇奈月観測所 1994年)流域面積 667 km2水源 鷲羽岳(富山市)水源の標高 2,924 m河口・合流先 日本海(黒部市、入善町)流域 日本 富山県 テンプレートを表示 黒部ダム �...