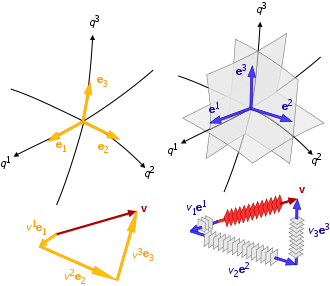
Base (álgebra linear)
|
Read other articles:

Railway Station in Andhra Pradesh Dharmavaram JunctionIndian Railways stationDharmavaram Junction signboardGeneral informationLocationDharmavaram, Anantapur district, Andhra Pradesh IndiaElevation371 mOwned byIndian RailwaysLine(s)Guntakal–Bangalore section, Dharmavarm–Pakala branch line, Dharmavaram-Satya Sai Prasanthi Nilayam-Penukonda line.Platforms5ConstructionParkingAvailableBicycle facilitiesYesOther informationStatusFunctionalStation codeDMMFare zoneSouth Central Railway zoneH...

artikel mungkin mengandung informasi sangat rinci yang menarik perhatian pembaca tertentu saja. Bantu kami dengan memecah atau memindahkan informasi relevan apapun dan menghapus informasi berlebihan yang bertentangan dengan kebijakan Wikipedia. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Fakultas KedokteranRumpun Ilmu KesehatanUniversitas IndonesiaSignature FK UI [1]MotoMedical Education and Research Excellent for Humanity[2]Moto dalam bahasa Indon...

Vice president of the United States from 1817 to 1825 This article is about the vice president of the United States. For the lead vocalist of the British progressive metal band TesseracT, see Tesseract (band). Daniel D. TompkinsOfficial Portrait c. 18176th Vice President of the United StatesIn officeMarch 4, 1817 – March 4, 1825PresidentJames MonroePreceded byElbridge GerrySucceeded byJohn C. Calhoun8th Governor of New YorkIn officeJuly 1, 1807 – February 24, 1817Lie...

Funk metalFaith No More tampil di Portugal pada tahun 2009Nama lain Thrash-funk punk-funk Sumber aliranFunk rockheavy metalmetal alternatif[1]thrash metal[2][3]Sumber kebudayaanPertengahan-1980an, Amerika SerikatBentuk turunanNu metalVersi regionalCalifornia[4]Versi lokalSan Francisco, California[5][6]Topik lainnya Groove metal rap metal Funk metal (juga dikenal sebagai thrash-funk[7] atau punk-funk)[8][9] adalah genre ca...

New Zealand political candidatesin the MMP era 1996 party lists by electorate 1999 party lists by electorate 2002 party lists by electorate 2005 party lists by electorate 2008 party lists by electorate 2011 party lists by electorate 2014 party lists by electorate 2017 party lists by electorate 2020 party lists by electorate 2023 party lists by electorate...

Medical conditionBacillary angiomatosisBartonella sp. (bacterial species which causes this condition)SpecialtyInfectious diseases Bacillary angiomatosis (BA) is a form of angiomatosis associated with bacteria of the genus Bartonella.[1] Symptoms Cutaneous BA is characterised by the presence of lesions on or under the skin. Appearing in numbers from one to hundreds, these lesions may take several forms:[citation needed] papules or nodules which are red, globular and non-b...

Head of the Catholic Church from 741 to 752 Pope Zacharias redirects here. For the Coptic Orthodox pope, see Pope Zacharias of Alexandria. Pope SaintZacharyBishop of RomeContemporary Byzantine fresco in Santa Maria AntiquaChurchChurch of RomePapacy began3 December or 5 December 741Papacy endedMarch 752PredecessorGregory IIISuccessorStephen IIOrdersConsecration4 or 6 December 741Created cardinal12 April 732by Gregory IIIPersonal detailsBorn679Santa Severina, Calabria, Eastern Roman EmpireDied1...

Scottish Gaelic orthography has evolved over many centuries and is heavily etymologizing in its modern form. This means the orthography tends to preserve historical components rather than operating on the principles of a phonemic orthography where the graphemes correspond directly to phonemes. This allows the same written form in Scottish Gaelic to result in a multitude of pronunciations, depending on the spoken variant of Scottish Gaelic. For example, the word coimhead ('watching') may resu...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

Comic book superhero This article is about the character known as Darna and Narda. For other characters given this name, as well as other uses, see Darna (disambiguation). Comics character DarnaTextless cover of Darna #1 (February 2003)Art by Ryan OroscoPublication informationPublisherAce Publications[1]First appearancePilipino Komiks, #77 (May 13, 1950)Created byMars RaveloNestor RedondoIn-story informationAlter egoNardaSpeciesTransformed human / Marte-an (extra-terrestrial) meldPlac...

Max-Planck-Gymnasium Nürtingen Schulform Gymnasium Schulnummer 04104292 Gründung 1914 Adresse Steinenbergstraße 17 72622 Nürtingen Land Baden-Württemberg Staat Deutschland Koordinaten 48° 37′ 47″ N, 9° 20′ 23″ O48.629729.33969Koordinaten: 48° 37′ 47″ N, 9° 20′ 23″ O Träger Stadt Nürtingen Schüler etwa 1.060 (2009) Lehrkräfte etwa 80 Leitung Petra Notz[1] Website www.mpg-nuertingen.de Da...

قاعة فنلنديا في هلسنكي. عمارة فنلندا لديها تاريخ ملحوظ يمتد على مدى 800 سنة [1] وقد ساهمت العمارة في العديد من الأساليب دولياً، مثل الحداثة الشمال أوروبية، من خلال أعمال ألفار آلتو.[2] ترتبط الإنجازات المعمار الفنلندي عموماً بالعمارة الحديثة، وذلك لأن أقل من 13٪ من الم�...

László Bölöni Personlig informationFullständigt namnLászló BölöniFödelsedatum11 mars 1953 (71 år)Födelseort Târgu Mureș, RumänienLängd176 cmKlubbinformationKlubb Panathinaikos (tränare)PositionTränare/ManagerSeniorlag* År1970–19841984–19871987–19881988–19891989–1992 Totalt Klubb ASA Targu Mures Steaua Bukarest Racing Jet Wavre Créteil US Orléans SM (GM) 406 (64)97 (24)16 0(0)11 0(2)77 0(4)607 (94) Landslag År1975–1988 Landslag Rumänien SM (GM)...

Квадрупла (от итал. quadruple — четверной) — курсовая монета итальянских государств, чеканившаяся в Папской области, Неаполе, Милане и других крупных городах Италии из высокопробного золота. Монета была эквивалентна четырем золотым скудо или двум золотым доппиям[1...

See also: Juvenilization of poverty Children living in poverty Two sisters sit on the slum streets of Spitalfields, London, circa 1903. Child poverty refers to the state of children living in poverty and applies to children from poor families and orphans being raised with limited or no state resources. UNICEF estimates that 356 million children live in extreme poverty. It is estimated that 1 billion children (about half of all children worldwide) lack at least one essential necessity such as ...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Fota railway station – news · newspapers · books · scholar · JSTOR (January 2015) (Learn how and when to remove this message) FotaFóiteGeneral informationLocationFota IslandIrelandCoordinates51°53′47″N 8°19′05″W / 51.8963°N 8.3181°W...

Donny van de Beek Situation actuelle Équipe Manchester United Numéro - Biographie Nationalité Néerlandaise Naissance 18 avril 1997 (27 ans) Nijkerkerveen (Pays-Bas) Taille 1,84 m (6′ 0″) Période pro. Depuis 2015 Poste Milieu de terrain Pied fort Droit Parcours junior Années Club -2008 Veensche Boys 2008-2015 Ajax Amsterdam Parcours senior1 AnnéesClub 0M.0(B.) 2015-2020 Ajax Amsterdam 175 (41) 2020- Manchester United 062 0(2) 2022 → Everton FC 007 0(1) 2024 → Ein...

Rugby playerHandré PollardPollard kicking a conversion at the 2015 Rugby World CupDate of birth (1994-03-11) 11 March 1994 (age 30)Place of birthSomerset West, South AfricaHeight189 cm (6 ft 2 in)Weight98 kg (216 lb; 15 st 6 lb)SchoolPaarl GimnasiumUniversityUniversity of PretoriaSpouse Marise Malherbe (m. 2017)ChildrenHunter André PollardRugby union careerPosition(s) Fly-half / Inside-CentreCurrent team Leicester Tiger...

1969 studio album by Donald ByrdFancy FreeStudio album by Donald ByrdReleasedDecember 1969[1]RecordedMay 9, June 6, 1969StudioVan Gelder Studio, Englewood Cliffs, New JerseyGenreJazz, jazz fusionLength39:10LabelBlue NoteProducerDuke PearsonDonald Byrd chronology The Creeper(1967) Fancy Free(1969) Electric Byrd(1970) Professional ratingsReview scoresSourceRatingAllMusic[2] Fancy Free is an album by American jazz trumpeter Donald Byrd that was recorded and released in 19...

Landform in Oakland County, Michigan For other uses, see Pine Knob (disambiguation). Pine KnobPine KnobIndependence Township, Michigan Highest pointElevation1,201 ft[1]Coordinates42°44′32″N 83°22′02″W / 42.7422524°N 83.3671629°W / 42.7422524; -83.3671629GeographyTopo mapUSGS 7.5' topographic mapPine Knob, Independence Township, Michigan[2]GeologyMountain typeSummit Pine Knob is a hill located in Independence Township in Oakland County, ...




















![{\displaystyle K[\alpha ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e3bdba98647a4f1fca648f0d76c3aa026ecdd55)




















