Combinação linear
|
Read other articles:

Chicago Film Critics Association Awards ke-3 diumumkan pada 7 maret 1991 di sebuah acara penghargaan yang diadakan di The Pump Room.[1] Acara tersebut menghargai pengabdian dalam pembuatan film tahun 1990. Nominasi-nominasinya diumumkan pada 20 Januari 1991.[1] Goodfellas meraih nominasi terbanyak (7), disusul oleh Dances With Wolves (4) dan The Godfather Part III (2).[1] Aktris Joan Cusack dan Kathy Bates masing-masing meraih dua nominasi.[1] Acara penghargaan...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Hubbul Amal ialah salah satu akhlak kepada diri sendiri yaitu salah satunya adalah hubbul amal. Hubbul amal atau yang biasa kita kenal dengan bekerja keras di perlukan dalam mencapai suatu hal atau dalam mencari rizki. Hubbul amal atau bekerja keras me...

Dominic BrianLahir26 November 1996 (umur 27)Surabaya, IndonesiaPekerjaanPenulisKebangsaanIndonesiaPendidikanInternational Design SchoolOrang tuaGidion Hindarto dan Debora Intan TrisnaKerabatGabriela Galice (adik) Dominic Brian (lahir 26 November 1996) adalah seorang penulis naskah komik Indonesia.[1] Dia sebelumnya terkenal berhasil mencatatkan namanya 2 kali dalam buku rekor dunia Guinness World Records setelah berhasil menunjukkan kemampuannya mengingat 76 deret angka dala...

Eure-et-Loir Departemen 28 Region Centre Prefecture Chartres Sous-prefecture ChâteaudunDreuxNogent-le-Rotrou Penduduk -total (1999) -Kepadatan penduduk Urutan 55407.66569 jiwa/km² Area 5.880 km² Arrondissement 4 Kanton 29 Kotamadya 403 President du Conseil general Albéric de Montgolfier Peta lokasi Eure-et-Loir ialah sebuah departemen di Prancis. Di departemen ini terletaklah Katedral Chartres. Katedral Chartres Pranala luar lbsKomune di departemen Eure-et-Loir Abondant Al...

Noah CyrusCyrus di MTV Video Music Awards tahun 2018Lahir8 Januari 2000 (umur 24)Nashville, Tennessee, Amerika SerikatPekerjaanPenyanyipenulis-laguaktrisTahun aktif2002–sekarangOrang tuaBilly Ray Cyrus (Ayah)Tish Cyrus (Ibu)KerabatMiley Cyrus (Saudara)Karier musikGenrePopelectrofolkInstrumenVokalLabelRECORDSSycoColumbia Noah Cyrus (lahir 8 Januari 2000)[1] adalah penyanyi, penulis lagu dan aktris asal Amerika Serikat. Pada tahun 2016, ia merilis single debutnya Make Me (C...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2023. Warren Eugene Brandon (2 November 1916 – 11 September 1977) adalah seorang pelukis dan fotografer California yang lahir di San Francisco. Biografi Ia belajar seni di Milligan College dan juga dengan Jack Davis, Ralph Ledesma, Jack Feld...

South Korean entertainment company This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: SM Entertainment – news · newspapers · books · scholar · JSTOR (August 2023) (Learn how and when to remove this template message) SM Entertainment Co., Ltd.Native nameSM 엔터테인먼트FormerlySM Studio (1989–1995)Company...

Component city in Leyte, Philippines Component city in Eastern Visayas, PhilippinesBaybayComponent cityCity of BaybayCity Hall FlagSealMotto: Our City. Our Home. Our FutureMap of Leyte with Baybay highlightedOpenStreetMapBaybayLocation within the PhilippinesCoordinates: 10°41′N 124°48′E / 10.68°N 124.8°E / 10.68; 124.8CountryPhilippinesRegionEastern VisayasProvinceLeyteDistrict 5th districtFounded1620Chartered1910CityhoodJune 16, 2007 (Lost cityhood in 200...

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Associazione Sportiva Lucchese Libertas 1905. Unione Sportiva LuccheseStagione 1922-1923Sport calcio Squadra Lucchese Presidente Prima Divisione9º posto nel girone C della Lega Nord. Retrocessa in Seconda Divisione. StadioCampo Sant'Anna 1921-1922 1923-1924 Si i...

Daerah Istimewa YogyakartaNama lengkapTim sepak bola Provinsi Daerah Istimewa YogyakartaStadionStadion Mandala Krida(Kapasitas: 35.000)LigaPONPra PON 2024Peringkat 2 di Grup B Kostum kandang Kostum tandang Tim sepak bola Provinsi Daerah Istimewa Yogyakarta atau Tim sepak bola Daerah Istimewa Yogyakarta adalah tim provinsial yang mewakili Daerah Istimewa Yogyakarta dalam cabang olahraga sepak bola pada Pekan Olahraga Nasional. Tim ini dikendalikan oleh Asosiasi Provinsi Persatuan Sepak bola Se...

Destroyer class of the US Navy This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Mitscher-class destroyer – news · newspapers · books · scholar · JSTOR (August 2009) (Learn how and when to remove this message) USS John S. McCain underway in early 1960s Class overview NameMitscher class Builders Bath Iron Works...

Fictional character from Happy Days Potsie redirects here. For other uses, see Potsy. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Potsie Weber – news · newspapers · books · scholar · JSTOR (April 2018) (Learn how and when to remove this message)Fictional character Potsie WeberPotsieFirst appearanceLove ...

1818 Proclamation This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Chilean Declaration of Independence – news · newspapers · books · scholar · JSTOR (February 2018) (Learn how and when to remove this message) Chilean Declaration of Independence document preserved at the National Congress of Chile, Valparaíso...
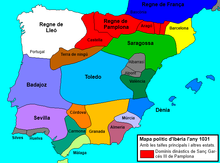
Communauté valencienne (ca) Comunitat Valenciana (es) Comunidad Valenciana Armoiries Drapeau Administration Pays Espagne Capitale Valence Statut d'autonomie 10 juillet 1982 Sièges au Parlement 33 députés18 (12 élus et 6 désignés)[1] sénateurs Président Carlos Mazón (PP) Pouvoir législatif Parlement valencien ISO 3166-2:ES ES-VC Démographie Gentilé Valencien, Valencienne Population 5 051 250 hab. (2021) Densité 217 hab./km2 Rang 4e rang (10,6 %) Géograp...

Twin Sisters of KyotoPoster Jepang asliNama lainJepang古都HepburnKoto SutradaraNoboru NakamuraProduserRyôtarô KuwataDitulis olehYasunari Kawabata (novel) Toshihide Gondo (permainan latar)PemeranShima Iwashita Hiroyuki Nagato Seiji MiyaguchiPenata musikToru TakemitsuSinematograferTôichirô NarushimaPenyuntingHisashi SagaraDistributorShochikuTanggal rilis 13 Januari 1963 (1963-01-13) (Jepang) Durasi107 menitNegaraJepangBahasaJepang Twin Sisters of Kyoto (古都code: ja...

Сельское поселение России (МО 2-го уровня)Новотитаровское сельское поселение Флаг[d] Герб 45°14′09″ с. ш. 38°58′16″ в. д.HGЯO Страна Россия Субъект РФ Краснодарский край Район Динской Включает 4 населённых пункта Адм. центр Новотитаровская Глава сельского пос�...
List of events in the year 1476 ← 1475 1474 1473 1472 1471 1476 in Ireland → 1477 1478 1479 1480 1481 Centuries: 13th 14th 15th 16th 17th Decades: 1450s 1460s 1470s 1480s 1490s See also:Other events of 1476 List of years in Ireland Events from the year 1476 in Ireland. Incumbent Lord: Edward IV Births John Alen, English-born canon lawyer, Archbishop of Dublin (d. 1534).[1] Deaths Brian Ó hUiginn, poet.[2] References ^ Alen, John (1476–1534), archbishop of Dubli...

Cet article traite uniquement de la compétition masculine. Pour la compétition féminine, voir Championnat d'Autriche de football féminin. Cet article traite uniquement de la compétition autrichienne. Pour la compétition Allemande, voir Bundesliga (Allemagne). Cet article est une ébauche concernant une compétition de football et l’Autriche. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Bundesliga Gén...

هذه مقالة غير مراجعة. ينبغي أن يزال هذا القالب بعد أن يراجعها محرر؛ إذا لزم الأمر فيجب أن توسم المقالة بقوالب الصيانة المناسبة. يمكن أيضاً تقديم طلب لمراجعة المقالة في الصفحة المخصصة لذلك. (نوفمبر 2021) يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه الم...

Irish republican women's paramilitary organisation Cumann na mBan Founded2 April 1914; 110 years ago (1914-04-02)HeadquartersIrelandIdeologyIrish republicanismIrish nationalismNational affiliationRepublican Sinn Féin (1986–present)Fianna Éireann (1914–present)Continuity Irish Republican Army (1986–present)ColoursGreenPolitics of the Republic of IrelandPolitical partiesElectionsPolitics of Northern IrelandPolitical partiesElections Part of a series onIrish republicani...
























