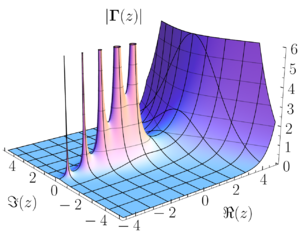
Plano complexo
|
Read other articles:

Shalom Dov WolpoNama asalשלום דוב וולפאLahir1948Nama lainSholom Ber WolpeWarga negaraIsraelPekerjaanRabiAktivis politikOrganisasiSOS IsraelPartai politikEretz Yisrael Shelanu Rabbi Shalom Dov Wolpo, atau Sholom Ber Wolpe, (Ibrani: שלום דוב וולפאcode: he is deprecated , kelahiran 1948) adalah seorang rabbi dan aktivis politik Israel. Wolpo adalah penulis lebih dari empat puluh buku.[1] Referensi ^ Efrat Weiss. Marzel, Rabbi Wolpo to run for Knesset. Y...

Church (tengah mengenakan jaket kulit) dengan Jenderal Walton Walker dan Jenderal J. Lawton Collins di Korea. Mayor Jenderal John Huston Church (28 Juni 1892 – 3 November 1953) adalah seorang perwira senior dalam United States Army. Ia berjuang dalam Perang Dunia I, Perang Dunia II dan Perang Korea. Referensi Portal Biografi Wikimedia Commons memiliki media mengenai John H. Church. Blair, Clay (1987). The Forgotten War: America in Korea, 1950–1953. New York: Times Books. ISB...

ChicagoPoster film ChicagoSutradaraRob MarshallProduserMartin RichardsDitulis olehBill CondonBerdasarkanChicagooleh Bob Fosse dan Fred EbbChicagooleh Maurine Dallas WatkinsPemeranRenée ZellwegerCatherine Zeta-JonesRichard GereQueen LatifahJohn C. ReillyPenata musikJohn KanderSinematograferDion BeebePenyuntingMartin WalshPerusahaanproduksiProducer Circle CompanyZadan/Meron ProductionsDistributorMiramax FilmsTanggal rilis 10 Desember 2002 (2002-12-10) (Samuel Goldwyn Theater) 27...

Artikel ini membahas mengenai bangunan, struktur, infrastruktur, atau kawasan terencana yang sedang dibangun atau akan segera selesai. Informasi di halaman ini bisa berubah setiap saat (tidak jarang perubahan yang besar) seiring dengan penyelesaiannya. Dubai Pearl merupakan sebuah komplek yang sedang dibangun di Dubai Media City di Dubai, Uni Emirat Arab. Komplek ini meliputi enam menara penghunian (dengan 2.000 apartemen), tiga menara hotel (dengan 1.500 kamar) dan dua menara perkantoran. Ko...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Untuk versi film, lihat The Great Passage. The Great Passage (舟を編むcode: ja is deprecated , Fune wo Amu) adalah sebuah serial anime Jepang yang diproduksi oleh Zexcs, anime ini diadaptasi dari novel yang ditulis oleh Shion Miura.[1] ser...

Heritage-listed railway station in Sydney, New South Wales, Australia St JamesElizabeth Street entranceGeneral informationLocationElizabeth Street, Sydney central business district, City of Sydney, New South Wales, AustraliaCoordinates33°52′13″S 151°12′43″E / 33.8702°S 151.2120°E / -33.8702; 151.2120Owned byTransport Asset Holding EntityOperated bySydney TrainsLine(s)City CircleDistance4.4 km (2.7 mi) from Central (clockwise) Platforms2 (1 island)...

PT Industri Kapal Indonesia (Persero)JenisBadan usaha milik negaraIndustriPerkapalanDidirikan29 Oktober 1977; 46 tahun lalu (1977-10-29)KantorpusatMakassar, Sulawesi SelatanWilayah operasiIndonesiaTokohkunciDiana Rosa[1](Direktur Utama)Soerjono[1](Komisaris Utama)ProdukKapalJasaPerbaikan kapalFabrikasi bajaPemilikPemerintah IndonesiaSitus webwww.ikishipyard.co.idPT Industri Kapal Indonesia (Persero) adalah sebuah badan usaha milik negara Indonesia yang bergerak di bidang ...

F-class submarine of the U.S. Navy, in service from 1912 to 1915 USS Skate (SS-23) redirects here. For other ships, see USS Skate. USS F-4 sometime between 1913 and 1915. History United States NameUSS F-4 BuilderThe Moran Company, Seattle, Washington Laid down21 August 1909, as USS Skate Launched6 January 1912 Commissioned3 May 1913 RenamedUSS F-4, 17 November 1911 Stricken31 August 1915 Fate Foundered, 25 March 1915 Raised, 29 August 1915; later a harbor marker and buried as trench fill off ...

List of largest LGBT eventsThe Stonewall Inn located in Greenwich Village was the site of the June 1969 Stonewall riots. That event in New York City's LGBT history has served as a touchstone for various social movements, as well as the catalyst for Pride parades around the world.[1][2][3]Frequencyannually, last Sunday in JuneLocation(s)New York CityInauguratedJune 28, 1970 (1970-06-28), as part of Christopher Street Liberation DayOrganized byHeritage of...

Pour les articles homonymes, voir Musée du jouet. Musée du jouet de ColmarInformations généralesType Musée du jouetOuverture 1993Surface 400 m2Visiteurs par an 72 289 (2016)Site web www.museejouet.comLocalisationPays FranceDivision administrative Haut-RhinCommune ColmarAdresse 40 rue Vauban 68000 ColmarCoordonnées 48° 04′ 46″ N, 7° 21′ 44″ Emodifier - modifier le code - modifier Wikidata Le musée du jouet est un musée consacré aux jo...

この項目には、一部のコンピュータや閲覧ソフトで表示できない文字が含まれています(詳細)。 数字の大字(だいじ)は、漢数字の一種。通常用いる単純な字形の漢数字(小字)の代わりに同じ音の別の漢字を用いるものである。 概要 壱万円日本銀行券(「壱」が大字) 弐千円日本銀行券(「弐」が大字) 漢数字には「一」「二」「三」と続く小字と、「壱」「�...

Politics of the Faroe Islands Constitution Constitution Act of Succession Freedom of Speech and the Press Taxation The Crown Monarch King Frederik X Privy Council Purveyors to the Royal Court The unity of the Realm Kingdom of Denmark Faroe Islands Denmark Greenland ExecutiveRegeringen The Government of Denmark High Commissioner (list) Lene Moyell Johansen Landsstýri The Government of the Faroe Islands Premier Aksel V. Johannesen Deputy Premier Høgni Hoydal Johannesen...

Día de los Caídos Lápidas del Cementerio Nacional de Arlington adornadas con banderas estadounidenses en un fin de semana del Día de los Caídos.LocalizaciónPaís Estados UnidosLocalidad Estados UnidosDatos generalesTipo día festivoPrimera vez 30 de mayo de 1868Fecha Último lunes de mayoMotivo muerto en combateSignificado Homenaje a los caídos en las guerras Día de los Presidentes Día de los Caídos Día de la Independencia de los Estados Unidos [editar datos e...

Ignatius dari Antiokhia, salah satu Bapa Kerasulan, adalah Patriark ketiga dari Antiokhia dan seorang murid dari Rasul Yohanes.[1] Dalam perjalanan ke Roma, Ignatius menulis serangkaian surat yang mencontohkan teologi Kristen yang sangat awal, membahas topik-topik seperti perubahan hari sabat, pengangkatan uskup, dan kritik terhadap yang disebut orang Yudais . Istilah Kristen proto-ortodoks atau proto-ortodoksi diciptakan oleh seorang sarjana Perjanjian Baru Bart D. Ehrman dan menggam...

هذه المقالة سلسلة حولالسياسة المحافظةفي الولايات المتَّحدة مدارس الرحيمة الماليَّة الاندماجيَّة الليبرتاريَّة الحراكيَّة الجدد الأصليون التقدميَّة الاجتماعيَّة التقليدويَّة الترامبيَّة مبادئ الخصوصية الأمريكيَّة ليبرالية كلاسيكية قيم عائلية سوق حر تجارة حرَّة قيم...

Yakima redirects here. For other uses, see Yakima (disambiguation). City in Washington, United StatesYakima, WashingtonCityYakima as viewed from Lookout Point SealNickname(s): The Palm Springs of Washington; The Heart of Central WashingtonLocation of Yakima in Yakima CountyYakima, WashingtonLocation in the United StatesCoordinates: 46°36′07″N 120°30′28″W / 46.60194°N 120.50778°W / 46.60194; -120.50778CountryUnited StatesStateWashingtonCountyYakimaIncor...

乔冠华 中华人民共和国外交部部长 中国人民对外友好协会顾问 任期1974年11月—1976年12月总理周恩来 → 华国锋前任姬鹏飞继任黄华 个人资料性别男出生(1913-03-28)1913年3月28日 中華民國江蘇省盐城县逝世1983年9月22日(1983歲—09—22)(70歲) 中华人民共和国北京市籍贯江蘇鹽城国籍 中华人民共和国政党 中国共产党配偶明仁(1940年病逝) 龚澎(1970年病逝) 章含�...

French-Canadian independent fur traders Coureur de bois, a woodcut by Arthur Heming (1870–1940) A coureur des bois in the painting La Vérendrye at the Lake of the Woods, circa 1900–1930 A coureur des bois (French: [kuʁœʁ de bwɑ]; lit. 'runner of the woods') or coureur de bois (French: [kuʁœʁ də bwɑ]; plural: coureurs de(s) bois) were independent entrepreneurial French Canadian traders who travelled in New France and the interior of North America, usually to...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (مارس 2018) مقاطعة وياندوت الإحداثيات 39°03′49″N 94°49′07″W / 39.063611111111°N 94.81861111111...

Biografi ini memerlukan lebih banyak catatan kaki untuk pemastian. Bantulah untuk menambahkan referensi atau sumber tepercaya. Materi kontroversial atau trivial yang sumbernya tidak memadai atau tidak bisa dipercaya harus segera dihapus, khususnya jika berpotensi memfitnah.Cari sumber: Aiman Witjaksono – berita · surat kabar · buku · cendekiawan · JSTOR (Mei 2024) (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Aiman WitjaksonoMasal...