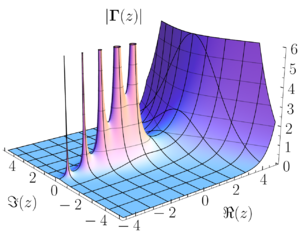
Análise complexa
|
Read other articles:

Anoa Pegunungan (Bubalus quarlesi) Anoa Pegunungan Status konservasi Terancam Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Mamalia Ordo: Cetartiodactyla Subordo: Ruminantia Famili: Bovidae Subfamili: Bovinae Genus: Bubalus Anoa pegunungan adalah salah satu dari dua jenis spesies anoa yang hidup di Indonesia. Mamalia ini dikenal juga dengan nama Mountain Anoa, Anoa de Montagne, Anoa de Quarle, Berganoa, dan Anoa de Montaña. Ciri-Ciri Panjang dari kepala sampai kaki 122–153&...

Gulat pada Pekan Olahraga Nasional 2016LokasiGOR Saparua, Kota BandungTanggal23–28 September 2016← 20122021 → Gulat pada Pekan Olahraga Nasional XIX akan dipertandingkan pada 23 sampai 28 september 2016[1] di GOR Saparua, Kompleks Olahraga Saparua, Kota Bandung, Jawa Barat. Gulat akan terbagi menjadi dua disiplin, gaya bebas dan Gaya Grego-Romawi, kemudian dibagi lagi kedalam kelas pertandingan berdasarkan berat badan. Untuk putra akan dipertandingkan masing-ma...

New World prehistoric projectile Clovis point, 11500–9000 BC, Sevier County, Utah, chert Clovis points are the characteristically fluted projectile points associated with the New World Clovis culture, a prehistoric Paleo-American culture. They are present in dense concentrations across much of North America and they are largely restricted to the north of South America. There are slight differences in points found in the Eastern United States bringing them to sometimes be called Clovis-like....

CullyfrazioneCully – Veduta LocalizzazioneStato Francia Regione Normandia Dipartimento Calvados ArrondissementCaen CantoneBretteville-l'Orgueilleuse ComuneMoulins en Bessin TerritorioCoordinate49°15′N 0°32′W / 49.25°N 0.533333°W49.25; -0.533333 (Cully)Coordinate: 49°15′N 0°32′W / 49.25°N 0.533333°W49.25; -0.533333 (Cully) Superficie6,46 km² Abitanti171[1] (2009) Densità26,47 ab./km² Altre informazioniCod. post...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Republik SingapuraInggris:Republic of SingaporeMelayu:Republik SingapuraMandarin:新加坡共和国Tamil:சிங்கப்பூர் குடியரசு Bendera Lambang Semboyan: Majulah Singapura (Melayu: Majulah Singapura)Lagu kebangsaan: Majulah Singapura Perlihatkan BumiPerlihatkan peta ASEANPerlihatkan peta BenderaLokasi Singapura (hijau)di ASEAN (abu-abu tua) – [Legenda]Ibu kotaKota Singapura1°17′N 103°50′E&#x...

У этого термина существуют и другие значения, см. Горностай (значения). Горностай Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:Челюстнороты...

2019 sci-fi film by Joko Anwar For other uses, see Gundala. GundalaTheatrical release posterDirected byJoko AnwarWritten byJoko AnwarBased onGundala by Harya Hasmi SuraminataProduced bySukhdev SinghWicky V. OlindoBismarka KurniawanStarring Abimana Aryasatya Tara Basro Bront Palarae Ario Bayu Rio Dewanto CinematographyIcal TanjungEdited byDinda AmandaMusic byAghi NarotamaBemby GustiTony MerleProductioncompaniesScreenplay FilmsBumilangit StudiosLegacy PicturesIdeosource EntertainmentDistributed...

Italian RepublicNuclear program start dateLate 1960s (ended in 1975)First nuclear weapon testNoneFirst thermonuclear weapon testNoneLast nuclear testNoneLargest yield testNoneTotal testsNonePeak stockpileNoneCurrent stockpileNoneCurrent strategic arsenalNoneCumulative strategic arsenal in megatonnageNoneMaximum missile rangeNoneNPT partyYesNuclear weapons program of Italy Weapons of mass destruction By type Biological Chemical Nuclear Radiological By country Albania Algeria Argentina Australi...

370–670 CE nomadic people who invaded India Not to be confused with Huns. Alchon Huns370–670 Portrait of Alchon king Khingila (c. 450 CE), and the bull/lunar tamga of the Alchon (known as Tamgha S1),[1] as visible on Alchon coinage. SanjeliEranGwaliorSondaniChoti SadriKuraKausambiRīsthalALCHONHUNSHEPHTHALITESNEZAKHUNSSASA-NIANSRAISGUPTASVAKATAKASZHANGZHUNGKINGDOMNorthern WeiTOCHARIANSclass=notpageimage| Find spots of epigraphic inscriptions (red dots) indicating local contr...

لمعانٍ أخرى، طالع مونت بليستانت (توضيح). مونت بليستانت الإحداثيات 41°06′N 73°48′W / 41.1°N 73.8°W / 41.1; -73.8 [1] تقسيم إداري البلد الولايات المتحدة[2][3] التقسيم الأعلى مقاطعة ويستتشستر خصائص جغرافية المساحة 84700000 متر مربع ارتفا�...

For other uses, see Jičín (disambiguation). Town in Hradec Králové, Czech RepublicJičínTownValdštejnovo Square FlagCoat of armsJičínLocation in the Czech RepublicCoordinates: 50°26′12″N 15°21′6″E / 50.43667°N 15.35167°E / 50.43667; 15.35167Country Czech RepublicRegionHradec KrálovéDistrictJičínFirst mentioned1293Government • MayorJan Malý (ANO)Area • Total25.86 km2 (9.98 sq mi)Elevation287 m (94...

梅拉蒂·达伊瓦·奥克塔维亚尼Melati Daeva Oktavianti基本資料代表國家/地區 印度尼西亞出生 (1994-10-28) 1994年10月28日(29歲)[1] 印度尼西亞万丹省西冷[1]身高1.68米(5英尺6英寸)[1]握拍右手[1]主項:女子雙打、混合雙打職業戰績48勝–27負(女雙)109勝–56負(混雙)最高世界排名第4位(混雙-普拉文·喬丹)(2020年3月17日[2])現時世界排名第...

Prize established in 1895 by Alfred Nobel For a list of the award's laureates, see List of Nobel laureates in Literature. AwardNobel Prize in LiteratureAwarded forOutstanding contributions in literatureLocationStockholm, SwedenPresented bySwedish AcademyReward(s)11 million SEK (2023)[1]First awarded1901Last awarded2023Currently held byJon Fosse (2023)Websitenobelprize.org ← 2022 · 2023 · 2024 → The Nobel Prize in Literature (here meaning for literatur...

State flag of South Dakota Location of South Dakota on the U.S. map This is a list of prominent people who were born in or lived for a significant period in U.S. state of South Dakota. For a larger list by location, see People from South Dakota. This is a dynamic list and may never be able to satisfy particular standards for completeness. You can help by adding missing items with reliable sources. Academia Vine Deloria Jr., American Indian author, theologian, historian, and activist Alvin Ha...

Questa voce sull'argomento motori aeronautici è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Piaggio P.XIIl Piaggio P.XI esposto presso il Museo dell'aeronautica Gianni CaproniDescrizione generaleCostruttore Piaggio Tiporadiale doppia stella Numero di cilindri14 Alimentazionecarburatore Schema impiantoCilindrata38,67 L Alesaggio146 mm Corsa165 mm CombustioneCombustibilebenzina 87 ottani Raffreddamento...

American comedy TV series (2023–present) BookieGenreComedyCreated by Chuck Lorre Nick Bakay Starring Sebastian Maniscalco Omar Dorsey Andrea Anders Vanessa Ferlito Jorge Garcia Maxim Swinton Charlie Sheen Opening themeBookie Theme SongEnding themeBookie Theme SongCountry of originUnited StatesOriginal languageEnglishNo. of seasons1No. of episodes8ProductionExecutive producers Chuck Lorre Nick Bakay Sebastian Maniscalco Judi Marmel Production locationLos Angeles County, California[1]...

Bride of the CenturyPoster promosi untuk Bride of the CenturyGenreKomedi Roman Fantasi MelodramaDitulis olehBaek Young-sookSutradaraYoon Sang-hoPemeranLee Hong-gi Yang Jin-sung Sung HyukNegara asalKorea SelatanBahasa asliKoreaJmlh. episode16ProduksiProduser eksekutifChoi Byung-hwaProduserJung Hyung-seo Jung Hoe-seokLokasi produksiKoreaRumah produksiAura MediaRilis asliJaringanTV ChosunRilis22 Februari (2014-02-22) –12 April 2014 (2014-4-12) Bride of the Century (Hangul:&...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) تصادم شرقي تامباكوندا الجويخطوط سايبا إنتركونتيننتال الجوية الرحلة 71، الخطوط الجوية السنغالية الرحلة 67...

Town in Kerala, India Village in Kerala, IndiaMalampuzha-IVillageMalampuzha-ILocation in Kerala, IndiaShow map of KeralaMalampuzha-IMalampuzha-I (India)Show map of IndiaCoordinates: 10°49′N 76°39′E / 10.817°N 76.650°E / 10.817; 76.650Country IndiaStateKeralaDistrictPalakkadGovernment • BodyMalampuzha Grama PanchayatArea • Total174.58 km2 (67.41 sq mi)Population (2011)[1] • Total11,879 •...