Read other articles:

SS JaguarJaguar1½—2½—3½ LitreJaguar 2½ litre sedan sport 1947InformasiProdusen SS Cars Jaguar Cars Masa produksi1935–1949PerakitanCoventry, EnglandBodi & rangkaKelasMobil Eksekutif (E)Tata letakFR layoutKronologiPendahuluSS Cars Ltd SS1PenerusJaguar Mark V Jaguar Mark IV (diucapkan mark four ) adalah jajaran mobil yang dibuat oleh Jaguar Cars dari tahun 1945 hingga 1949. Mobil ini dipasarkan sebagai Jaguar 1½ litre, Jaguar 2½ litre dan Jaguar 3½ litre dengan nama Mark IV kemu...

Tritunggal Kudus, Jan Cornelisz Vermeyen, abad ke-16 Ekonomi Keselamatan, yang juga disebut Ekonomi Ilahi, adalah bagian dari wahyu ilahi dalam tradisi Kristen yang menyinggung soal kisah Allah menciptakan dan mengurus dunia, terutama rencana keselamatan-Nya melalui Gereja. Dari kata Yunani oikonomia (ekonomi), yang artinya, kepengurusan rumah tangga.[1] Ini adalah unsur dan sumber daya yang diwahyukan oleh Allah sebagai kebutuhan untuk keselamatan melalui wahyu khusus, kitab suci Per...

Pour les articles homonymes, voir Citron (homonymie). Pour l’article ayant un titre homophone, voir Cytron. Citron Plante Citronnier Espèce Citrus limon (L.) Origine Proche-Orient et Italie pour les cultivars acides Vitamines Vitamine C, vitamine B1, vitamine B2, vitamine B3, vitamine B5, vitamine B6, vitamine A, vitamine E, Minéraux Calcium, fer, magnésium, phosphore, potassium, Cuivre, sodium, zinc modifier  Deux citrons jaunes, un entier et un coupé en deux. Fleur de citronnier...

← Lamed Mem Nun → Fenisia Ibrani Aram Suryani Arab מ,ם ܡܡ م‍,م Alfabetturunan Yunani Latin Kiril Μ M М Representasi fonemik: m Urutan dalam alfabet: 13 Nilai huruf/Gematria: 40 Mem (juga dieja Meem atau Mim) adalah huruf ke-13 dalam banyak abjad rumpun bahasa Semit, termasuk abjad Fenisia, abjad Aram, abjad Ibrani מ dan abjad Arab mīm م. Nilai bunyinya adalah [m]. Huruf Fenisia menghasilkan Alfabet Yunani Mu (Μ), Alfabet Etruscan 𐌌,Alfabet Latin M, dan Alfabet Ki...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Un appelé de l’infanterie équipé d'un mousqueton Lebel R35 et coiffé d'un casque Modèle 1951. De 1954 à 1962, un nombre grandissant d'appelés du contingent, nés entre 1932 et 1943, est envoyé en Algérie pour participer à la guerre d'Algérie, commencée le 1er novembre 1954. Durant toute la période de la guerre, la France mobilise au total 1,5 million d’appelés du contingent (au sein d'une armée de 2 millions de soldats)[1]. La mobilisation générale durant la guerre d'Alg�...

Voce principale: Law & Order - Unità vittime speciali. Il cast principale durante la quattordicesima stagione:Dann Florek (Cap. Donald Cragen), Danny Pino (Det. Nick Amaro), Mariska Hargitay (Det. Olivia Benson), Kelli Giddish (Det. Amanda Rollins), Richard Belzer (Serg. John Munch) e Ice-T (Det. Odafin Tutuola). La quattordicesima stagione della serie televisiva Law & Order - Unità vittime speciali, composta da 24 episodi, è stata trasmessa in prima visione negli Stati Uniti da N...

For other ports with similar names, see Port Richmond. Port in United StatesPort of RichmondPort of RichmondClick on the map for a fullscreen viewLocationCountryUnited StatesLocationRichmond, CaliforniaCoordinates37°54′54″N 122°21′40″W / 37.915°N 122.361°W / 37.915; -122.361UN/LOCODEUSRCH[1]DetailsOpened1980Land area200 acres (0.81 km2)StatisticsVessel arrivals(CY )Annual cargo tonnage21.9 million metric revenue tons (CY 2010)[2]Value ...

Закон Смута — Хоули о тарифе (англ. The Smoot–Hawley Tariff Act, иногда упоминается как Закон Хоули — Смута (англ. The Hawley–Smoot Tariff Act), 1930) — американский закон о таможенном тарифе, подписанный президентом США 17 июня 1930 года. Законом поднимались ставки пошлин на более чем 20 ты�...

У Вікіпедії є статті про інші населені пункти з такою назвою: Федорівка. село Федорівка Країна  Україна Область Одеська область Район  Подільський район Громада Окнянська селищна громада Код КАТОТТГ UA51120150480011627 Основні дані Засноване 1840 Населення 44 Площа 0,25 км² Г�...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Patung dada Perlasca di Budapest Giorgio Perlasca (13 Januari 1910 – 15 Agustus 1992) adalah seorang pengusaha dan mantan fasis Italia. Dengan kolaborasi para diplomat resmi, ia menjabat sebagai konjen Spanyol untuk Hungaria pada musim...

إقليم أوسردمعلومات عامةالاسم الأصل ‫إقليم أوسرد‬ (بالعربية) ⵜⴰⵎⵏⴱⴰⴹⵜ ⵏ ⴰⵡⵙⴻⵔⴷ (بالأمازيغية معيارية مغربية) البلد المغرب العاصمة أوسرد تقع في التقسيم الإداري جهة الداخلة وادي الذهب المنطقة الزمنية ت ع م+01:00 الإحداثيات 20°49′59″N 17°06′00″W / 20.8331°N 17.1°W / 20.8...

此條目可参照英語維基百科相應條目来扩充。 (2019年9月9日)若您熟悉来源语言和主题，请协助参考外语维基百科扩充条目。请勿直接提交机械翻译，也不要翻译不可靠、低品质内容。依版权协议，译文需在编辑摘要注明来源，或于讨论页顶部标记{{Translated page}}标签。 此條目没有列出任何参考或来源。 (2019年9月9日)維基百科所有的內容都應該可供查證。请协助補充可靠来源以...

Chữ Kirin DjeHệ chữ KirinMẫu tự SlavАБВГҐДЂЃЕЀЁЄЖЗЗ́ЅИЍІЇЙЈКЛЉМНЊОПРСС́ТЋЌУЎҮФХЦЧЏШЩЪЫЬЭЮЯMẫu tự ngôn ngữ phi SlavӐА̄А̊А̃ӒӒ̄ӘӘ́Ә̃ӚӔҒГ̧Г̑Г̄ҔӺӶԀԂꚂꚀꚈԪԬӖЕ̄Е̃Ё̄Є̈ӁҖꚄӜԄҘӞԐԐ̈ӠԆӢИ̃ҊӤҚӃҠҞҜԞԚӅԮԒԠԈԔӍӉҢԨӇҤԢԊО̆О̃О̄ӦӨӨ̄ӪҨԤҦР̌ҎԖҪԌꚐҬꚊꚌԎУ̃ӮӰӰ́ӲҮҮ́ҰХ̑ҲӼӾҺҺ̈ԦꚔҴꚎҶӴӋҸꚒꚖꚆҼҾЫ̆Ы̄ӸҌЭ̆Э̄Э̇...

Not to be confused with Northern Lights. 1999 single by Super Furry AnimalsNorthern LitesSingle by Super Furry Animalsfrom the album Guerrilla Released10 May 1999RecordedReal World Studios, Box, WiltshireGenre Alternative rock calypso Length3:31LabelCreation RecordsSongwriter(s)Super Furry AnimalsProducer(s)Super Furry AnimalsSuper Furry Animals singles chronology Demons (1997) Northern Lites (1999) Fire in My Heart (1999) Northern Lites is the ninth single by Super Furry Animals. It was the ...

Ferdinand LöweFerdinand Löwe en 1898.BiographieNaissance 1863 ou 19 février 1865VienneDécès 6 janvier 1925VienneSépulture Cimetière central de VienneNationalité autrichienneActivités Chef d'orchestre, compositeurAutres informationsA travaillé pour Académie de musique et des arts du spectacle de Vienne‎Membre de Orchestre symphonique de VienneInstrument PianoGenre artistique Musique classiqueVue de la sépulture.modifier - modifier le code - modifier Wikidata Ferdinand Löwe est u...

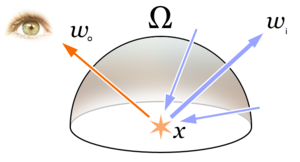
Integral equation The rendering equation describes the total amount of light emitted from a point x along a particular viewing direction, given a function for incoming light and a BRDF. In computer graphics, the rendering equation is an integral equation in which the equilibrium radiance leaving a point is given as the sum of emitted plus reflected radiance under a geometric optics approximation. It was simultaneously introduced into computer graphics by David Immel et al.[1] and Jame...

NGC 1763 La nébuleuse en émission NGC 1763. Données d’observation(Époque J2000.0) Constellation Dorade[1] Ascension droite (α) 04h 56m 49,2s[2] Déclinaison (δ) −66° 24′ 33″ [2] Dimensions apparentes (V) 5,0′ x 3,0′[3] Localisation dans la constellation : Dorade Astrométrie Distance environ 48,5 kpc (∼158 000 al) [4] Caractéristiques physiques Type d'objet Nébuleuse en émission Galaxie hôte Grand Nuage de Mage...

French mathematician (1795–1870) You can help expand this article with text translated from the corresponding article in French. (December 2012) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-tra...

The examples and perspective in this article may not represent a worldwide view of the subject. You may improve this article, discuss the issue on the talk page, or create a new article, as appropriate. (September 2023) (Learn how and when to remove this message) Part of a series onMagic Background History of magic Magic and religion Psychological theories of magic Forms Apotropaic magic Black magic Ceremonial magic Chaos magic Divination Evocation Goetia Gray magic Invocation Natural magic ...