Regulær mangekant
|
Read other articles:

Rwandan passport (Pasiporo y'u Rwanda)TypePassportIssued by RwandaPurposeIdentification and Traveling document IdentificationValid inThis passport is valid for all countriesEligibilityRwandan citizenshipExpiration5 or 10 years The Rwandan passport is issued to Rwandan citizens for international travel. Rwanda started issuing East African Community Biometric Passport also known as E-Passport(With which entry to all east African countries is visa-free) in June 2019 replacing the old ones t...

SM InstituteJenisPublikIndustriPendidikan musikModelArtisK-popDidirikan2021Kantorpusat SeoulTokohkunciLee Sung SuTak Young JunIndukSM EntertainmentSitus webSM Institute Offcial SM Institute adalah lembaga pendidikan berskala global yang diperuntukkan untuk para siswa yang tertarik dengan dunia hiburan. Program yang ditawarkan termasuk formula SM Entertainment yang terbukti efektif dalam melahirkan individu bertalenta untuk menjadi bintang K-Pop ternama. Mereka juga akan memberikan keahlian pe...
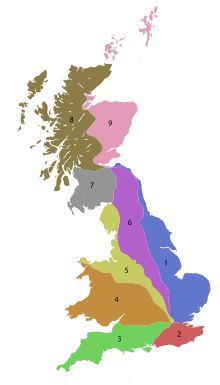
Class of road in Great Britain's Zone 8 The numbering zones for A-roads in Great Britain List of A roads in zone 8 in Great Britain starting north of the A8 and west of the A9 (roads beginning with 8). Single- and double-digit roads Road From To Notes A8 Greenock Edinburgh 25-mile (40-kilometre) gap between Newbridge and Newhouse A80 Glasgow Moodiesburn A81 Glasgow Callander A82 Glasgow Inverness A83 Tarbet Campbeltown A84 Stirling Lochearnhead A85 Oban Dundee A86 Spean Bridge Kingussie A87 I...

Subprefecture and commune in Occitania, FranceFlorac Trois Rivières Florac-Tres-Rius (Occitan)Subprefecture and communeLocation of Florac Trois Rivières Florac Trois RivièresShow map of FranceFlorac Trois RivièresShow map of OccitanieCoordinates: 44°19′26″N 3°35′38″E / 44.324°N 3.594°E / 44.324; 3.594CountryFranceRegionOccitaniaDepartmentLozèreArrondissementFloracCantonFlorac Trois RivièresIntercommunalityGorges Causses CévennesGovernment ...

Zhu Wen Zhu Quanzhong (Hanzi: 朱全忠, 852-912), terlahir dengan nama Zhu Wen (朱温), adalah seorang gubernur militer pada tahun-tahun terakhir Dinasti Tang. Dia adalah mantan bawahan pemberontak Huang Chao yang kemudian membelot pada Tang setelah kekalahan Huang sudah di depan mata. Sejak itu dia diberikan nama kehormatan Quanzhong yang artinya kesetiaan penuh oleh Kaisar Tang Xizong. Tahun 907, dia menggulingkan Dinasti Tang yang telah lemah dan mendeklarasikan diri sebagai kaisar dari ...

Artikel ini perlu diterjemahkan ke bahasa Indonesia. Artikel ini ditulis atau diterjemahkan secara buruk dari Wikipedia bahasa selain Indonesia. Jika halaman ini ditujukan untuk komunitas berbahasa tersebut, halaman itu harus dikontribusikan ke Wikipedia bahasa tersebut. Lihat daftar bahasa Wikipedia. Artikel yang tidak diterjemahkan dapat dihapus secara cepat sesuai kriteria A2. Jika Anda ingin memeriksa artikel ini, Anda boleh menggunakan mesin penerjemah. Namun ingat, mohon tidak menyalin ...

Stasiun Manggarai A01B09C13 Tampak depan perspektif Stasiun Manggarai sisi timur dengan teks bertuliskan Stasiun Sentral Manggarai pada bangunan lama, Maret 2024LokasiJalan Manggarai Utara 1Manggarai, Tebet, Jakarta Selatan, 12850IndonesiaKoordinat6°12′28″S 106°51′10″E / 6.20778°S 106.85278°E / -6.20778; 106.85278Koordinat: 6°12′28″S 106°51′10″E / 6.20778°S 106.85278°E / -6.20778; 106.85278Ketinggian+13 mOperator KAI Comm...

Untuk roti isi Elvis serupa, lihat roti lapis daging babi, pisang, dan selai kacang. Fool's Gold LoafJenisRoti isiTempat asalAmerika SerikatDaerahDenver, ColoradoDibuat olehColorado Mine CompanyBahan utamaRoti, krim selai kacang, jeli anggur, daging babiEnergi makanan(per porsi )~8,000[1] kkalSunting kotak info • L • BBantuan penggunaan templat ini Fool's Gold Loaf adalah sebuah roti lapis yang dibuat oleh Colorado Mine Company, sebuah restoran di Denver, Colorado. ...

Untuk film sebelumnya, lihat A Strange Adventure (film 1932). A Strange AdventurePoster rilis teatrikalSutradaraWilliam WitneyProduserWilliam J. O'SullivanSkenarioHouston BranchPemeranJoan EvansBen CooperMarla EnglishJan MerlinNick AdamsPeter MillerPenata musikR. Dale ButtsSinematograferBud ThackeryPenyuntingHoward A. SmithPerusahaanproduksiRepublic PicturesDistributorRepublic PicturesTanggal rilis 24 Agustus 1956 (1956-08-24) Durasi70 menitNegaraAmerika SerikatBahasaInggris A Stra...

1961 novel by Stanisław Lem Solaris Cover of the first editionAuthorStanisław LemCover artistK.M. SopoćkoCountryPolish People's RepublicLanguagePolishGenreScience fictionPublisherMON, Walker (US)[1]Publication date1961Published in English1970Media typePrint (hardcover and paperback) AudioPages204ISBN0156027607OCLC10072735Dewey Decimal891.8/537 19LC ClassPG7158.L392 Z53 1985 Solaris is a 1961 science fiction novel by Polish writer Stanisław Lem. It follows a cr...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

Raja-udang Biru Alcedo coerulescensdari Muara Cikeas, Babelan, Bekasi Status konservasi Risiko Rendah (IUCN 3.1)[1] Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Aves Ordo: Coraciiformes Famili: Alcedinidae Genus: Alcedo Spesies: A. coerulescens Nama binomial Alcedo coerulescensVieillot, 1818[2] Raja-udang biru[3] atau burung udang biru[4] (Alcedo coerulescens) adalah spesies burung dari keluarga Alcedinidae, dari genus Alcedo. Burung...

خسوف القمر سبتمبر 2016 معلومات عامة نوع الخسوف خسوف شبه الظل القدر 1.0548 التاريخ 16 سبتمبر 2016 مرئي في ايطاليا غاما 1.3638- بُعد القمر 379,104 كيلومتر قطر القمر 0.525° - 0.534° ساروس 147 قطر الشمس 0.524° الفترات (hh:mm:ss) شبه الظل 02:45:00 التوقيتات (ت ع م) بداية جزئي (P1) 16:54:40 بداية كلي (U1) 18:54:17 الذروة 20:53:57 ...

Tonight Show RamadanGenreGelar wicaraBerdasarkanThe Tonight Show Starring Jimmy Fallon (NBC)PresenterVincent RompiesDeddy Mahendra DestaHesti PurwadinataEnzy StoriaHusein Ja'far Al HadarNegara asalIndonesiaBahasa asliBahasa IndonesiaProduksiLokasi produksiSound Stage NET., Graha Mitra, Karet Semanggi, Setiabudi, Jakarta SelatanDurasi60 menitRumah produksiNET. EntertainmentDistributorNet Visi MediaRilis asliJaringanNET.Format gambarHDTV (1080i 16:9)Format audioDolby Digital 5.1Rilis13 April 2...

International volleyball tournamentVolleyball competition held in South Korea 2022 FIVB Volleyball Men's Challenger Cup서울 2022 FIVB 발리볼챌린저컵Seoul, host cityTournament detailsHost nation South KoreaCitySeoulDates28–31 JulyTeams8 (from 5 confederations)Venue(s)1 (in 1 host city)Champions Cuba (1st title)Runners-up TurkeyThird place South KoreaFourth place Czech RepublicTournament statisticsMatches played8Attendance14,200 (1,775...
State of Australia State in AustraliaWestern AustraliaState FlagCoat of armsNickname(s): The Wildflower StateThe Golden State QLD NSW ACT WA NT SA VIC TAS Location of Western Australia in Australia26°S 121°E / 26°S 121°E / -26; 121CountryAustraliaBefore federationColony of Western AustraliaEstablished as the Swan River Colony2 May 1829Responsible government21 October 1890Federation1 January 1901Capitaland largest cityPerthAdministration139 local government are...
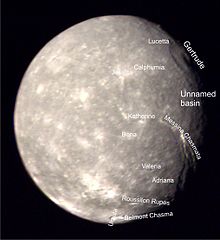
Crater on Uranus's moon Titania 12°24′S 45°12′E / 12.4°S 45.2°E / -12.4; 45.2[1] Ursula is a large bright crater near the bottom of this Voyager 2 image. Ursula is a large crater on Uranus's moon Titania. It is about 135 km across, and is cut by Belmont Chasma.[1] It is named after Hero's attendant in William Shakespeare's comedy Much Ado About Nothing.[1][a] Ursula has a central pit with diameter of about 20 km. It is ...

This article needs to be updated. Please help update this article to reflect recent events or newly available information. (April 2020)Sounddogs.comType of siteSound effects library, production music libraryAvailable inEnglishHeadquartersRichmond Hill, Ontario, Canada[1]Country of originCanadaArea servedWorldwideOwnerSound Ideas[2]URLwww.sounddogs.comLaunchedMay 1, 1997; 27 years ago (1997-05-01) [3]Current statusActive Sounddogs.com, I...
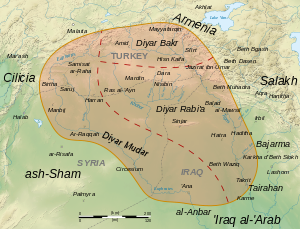
Map of the Jazira (Upper Mesopotamia), with its provinces, in medieval times Diyar Rabi'a (Arabic: دِيَارُ رَبِيعَةَ, romanized: Diyār Rabīʿa, lit. 'abode of Rabi'a') is the medieval Arabic name of the easternmost and largest of the three provinces of the Jazira (Upper Mesopotamia), the other two being Diyar Bakr and Diyar Mudar. According to the medieval geographer al-Baladhuri, all three provinces were named after the main Arab tribes that were settled ...

هشام الهاشمي هشام الهاشمي ضيف قناة التغيير في 27 نيسان 2020، قبل اغتياله بشهرين و9 أيام معلومات شخصية الميلاد 9 مايو 1973 بغداد الوفاة 6 يوليو 2020 (47 سنة) [1][2] زيونة سبب الوفاة إصابة بعيار ناري مكان الدفن مقبرة وادي السلام مواطنة الجمهورية العراقية (1973–...