|
õ¯ (šÚ)
![]() ššÇš šš Šõý§õ¿šÏ Š¯šõ°Š¯ˋÚËš¥ŠÀ ŠýšÇšÏ š ŠŠË¥ õ¯ŠŠ¥ ÚŠÊ ššÇš šš Šõý§õ¿šÏ Š¯šõ°Š¯ˋÚËš¥ŠÀ ŠýšÇšÏ š ŠŠË¥ õ¯ŠŠ¥ ÚŠÊ
õ¡¯ÚÚšš, õ¯(ÒÏ ššÇ: angle)š õ¯š Šš š õ¯Š Š Š¯šÏš šÇ šÇŠÈ´Š ŠÚšÇŠÊ. šÇ Šš š õ¯š õ¥ÙšÏš (-Õ£, ššÇ: vertex)šÇŠ¥õ° ÚŠˋ¯, Š Š¯šÏš š õ¯š Š°(Õ, ššÇ: side)šÇŠ¥õ° ÚŠÊ. õ¯š Š Š°šÇ ŠýšÇšÏ š Š, šÎ õ¯š Ú˜õ¡¯ŠË¥ ŠÚŠÇŠ šš õ¯Š(ÒÏͤÎ)Š¥õ° ÚŠÊ. šŠ¯Úõý ŠÏÚŠˋÇ, ššÇš šš Šõý§õ¿šÏ šõ° Š¯ŠŠ¯ˋÚËš¥ŠÀ ŠýšÇšÏ š ŠšÇŠÊ. Š°ÇÚç õ¯šÇŠ¥õ° ÚŠˋÇ ÚŠˋÇššš š šŠŠ õýš ŠÏÚšÏŠÏ 3š¯´š õ°çõ¯šš ŠÏÚŠ š
šýÇõ¯Š š šÚ š šŠÊ.
šÂ
ŠË
õ¡¯ÚÚšš õ¯(ÒÏ, angle)š ÚŠˋÇšš Š šÏš šÇ šŠÀ ŠÏŠ õ皯´ŠË¥ šÇŠÈ¯ Š õñ¡ Š šÏš ŠÊšÇ šŠÀš ŠÚÇ ŠýšÇšÏ š ŠŠË¥ õ¯šÇŠ¥ Úõ° šÇŠ˜Ú õ¯š Ú˜õ¡¯ŠË¥ õ¯Š(ÒÏͤÎ)Š¥õ° ŠÑŠË¡ŠÊ.[1]
õñ¡Š˜Š šÇŠ˜Ú šõýˋÚ š šš šÚŠÊŠˋÇ Š šÏš šÇ šŠÀ Ú šÏš ššš š¥š¿ÚšÏ šŠ Ú õ皯´ŠŠ õ¯š šŠÀ ššˆ§š¥ŠÀ 2õ¯šˋš õ¯šÇ šõý´ ÚÙš 4õ¯õ¯ ŠÚŠõýŠŠ₤ŠÀ šÂÚÚŠˋÇšš 0š š õ¡¯šÊš¥ŠÀ Šš š õ¯Š Š Š¯šÏš š õ¯š Úš˜ Š´ ÚŠš õ¯š õ¯Š õý§š¯ŠË¥ õ¯š Ú š šŠÊ.
šÇõýš Š šÏš š õ¯ Šš ŠÊ šÊ õ¯š Š¯ˋÚËš Šš ŠÊšÇ Ú š šš ŠÏŠõý ŠŠ õýš šŠ₤¡ÚŠÊ.[2]
šÇšýŠ¥ õ¯š ÚŠˋÇ šš Š šÏš ŠÊšÇ šŠÀš ŠÚÇ õ¡¯š¡šÇšÏ š ŠŠË¥ ÚÚÚ õýšÇšÏŠÏ šÂÚÚŠˋÇ šš x, yšÑ šÇš¡š zšÑ ŠÝš šÎõ¯ŠË¥ šÑõ¯š š¥ŠÀ šÊš Ú´š¥ŠÀš´ 3š¯´š õ¯š š
šýÇõ¯šÇ õ¿šÇŠ ŠŠÊŠË¡ šÝšÏš ÚÚÚŠŠÀ õ¯š Ú šŠ šŠÊ.
Ú˜õ¡¯š Š¯ŠË¡ õ¯
- šÏõ¯(ÓÇÒÏ, right angle)
- Šõ¯(ÕÒÏ, obtuse angle)
- šõ¯(Õ°ÒÏ, acute angle)
- Úõ¯(Í¿°ÒÏ, straight angle)
- šõ¯(Í¿ÒÏ, reentering angle): 180ŠŠ°ÇŠÊ Ú˜õ° 360ŠŠ°ÇŠÊ šš õ¯
- šý õ¯(Í¡ÒÏ, convex angle): 180ŠŠ°ÇŠÊ šš õ¯
- Š¿õ¯(-ÒÏ, =š˜õ¯(ÌÒÏ), Š¿õ¡Çõ¯, oblique angle): šõ¯ ŠŠ Šõ¯šýŠ¥ šÏõ¯šÇŠ Úõ¯šÇ šŠ õý§š˜(õ¡¯š¡õ¡¯)õ¯ šŠ õ¯š¥ŠÀ šõ¯ ŠŠ Šõ¯ ŠÝšÇ šÇš ÚÇŠ¿ÚŠÊ.
- Š¯ÚÇ(Turn (geometry)): 360Š
- šÈ¥õ¯(Í´ÒÏ, round angle): ŠÊõ¯Ú ŠŠ š õ¯
šÏš š õ皯´ŠÀ šÇŠÈ´šÇšÏŠ õ¯

- š¯õ¯(͈ÒÏ, reflex angle, major angle): šŠË¥ ŠÊŠˋÇ Ú š šš ŠšÊŠ Š Š¯šÏš šÇ šÇŠÈ´Š õ¯šš Š°ÇŠÊ Ú¯ šˆ§š õ¯š¡ Š¯õ¿Ëšˆ§ õ¯š š¯õ¯šÇŠ¥õ° ŠÑŠË¡ŠÊ.[3] šÇŠ ššˆ§š šÇŠÈ´Š õ¯š Úõ¯Š°ÇŠÊ šõ¡¯š š¯õ¯š 180ŠŠ°ÇŠÊ Ú˜ŠÊ.
- šÇõ¯(ÍÈÒÏ, minor angle): šŠË¥ ŠÊŠˋÇ Ú š šš ŠšÊŠ Š Š¯šÏš šÇ šÇŠÈ´Š õ¯šš Š°ÇŠÊ šš šˆ§š õ¯š¡ ššˆ§ õ¯š šÇõ¯šÇŠ¥õ° ÚŠÊ.
- š˜õ¯(ÕÊÒÏ, complementary angle): šõ¯š ŠÚÇ, ŠÚš˜ šÏõ¯šÇ ŠŠ õ¯š õñ¡ šõ¯š š˜õ¯(complementary angle)šÇŠ¥õ° ÚŠÊ.
- Š°Çõ¯(ÒÈÒÏ, supplementary angle): Úõ¯Š°ÇŠÊ šš õ¯ŠŠË¥ õ¯šÏŠ õ¯š ŠÚÇ, ŠÚš˜ Úõ¯šÇ Šõý ÚŠ õ¯š Š°Çõ¯(supplementary angle)šÇŠ¥õ° ÚŠÊ.
- õ°çšÀõ¯(Í
ÝÒ£ÒÏ, explementary angle): šŠÀ ŠÚš˜ šŠŠ 360ŠŠË¥ šÇŠÈ´Š õ¯ŠÊš ŠÚÇš õ°çšÀõ¯šÇŠ¥ ÚŠÊ.
- ŠÏõ¥ÙšÏõ¯(=Šš õ¯(Í¯Õ ÒÏ))
- Š¥š¡õ¯(--ÒÏ, =Úõ¯(ÍʃÒÏ), contained angle)=š˜šõ¯: šõ¯š¥õ¯Ú, ŠÇÚšÝõ°¥ š¡ÚšÝš õ°çš õÑÊŠ, šŠ¢õ°Àš ŠÝšš ŠÊŠÈ´šÇšÏŠÊ.
- õçõ¯(ð¤ÊÒÏ, =ŠÏŠõ¯, angle of intersection): Š šÏš šÇ ŠÏŠ šŠÀš š ŠÑš šŠÑÚ´š¥ŠÀš´ õ¯Šõ¯ šõ¡ÇŠÊ.
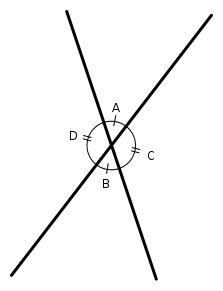
ŠÚšš šÇŠÈ´šÇšÏŠ õ¯
- ŠÇõ¯(Í
ÏÒÏ, =šõ¯, interior angle)
- š¡õ¯(ÍÊÒÏ, =Š¯Ùõ¯, exterior angle)
- Šõ¯(ͯÒÏ, opposite angle): šŠÀ ŠÏšÈ¥Š°ÇŠ õ¯š¥ŠÀ Šš¿Ùõ¯, ŠÏõ¯, ŠÏŠˆ´, ŠÏš õ¯, ŠÏšõ¯š¥ŠÀŠ ŠÑŠÎ¯ŠÊ[4], Ú¿Ú ŠÊõ¯Ú ŠÇšš Ú õ¯ ŠŠ Ú Š°õ°¥ šŠÀ ŠÏšÈ¥ ŠÚš˜ šŠ õ¯
- ŠÇŠõ¯(Í
ÏͯÒÏ, =šŠÏõ¯, interior opposite angle): š¥õ¯Ú ŠÝšš Ú š¡õ¯š ŠÚš˜ šÇšõ¯(š¡š Ú ŠÇõ¯)šÇ šŠ ŠÊŠË¡ ŠÇõ¯ŠÊ
- Š¯õ¯(-ÒÏ, base angle): ŠÝŠ°š˜ŠÊŠÎ˜õ¥Ç, šÇŠÝŠ°š¥õ¯Úš šÝšÏšš ŠÊŠÈ´šÇšÏŠÊ.
- šÇšõ¯(--ÒÏ, adjacent angles, =š¡š õ¯): ŠÇõ¯õ°¥ š¡õ¯š šÝšÏ ŠÝšš ŠÊŠÈ´šÇšÏŠÊ.
- ÚŠˋÇõ¯(Í¿°ÕÂÒÏ, =šÇŠˋÇõ¯, plane angle)
- ŠÊŠˋÇõ¯(ÍÊÕÂÒÏ, polyhedral angle): ŠÊŠˋÇšýÇšš ŠÚŠŠ õ¯
ššš šÝŠÎ§ÚŠ õ¯
- ššÈ¥õ¯(ÍÍ´ÒÏ, =šŠŠ õ¯): šš ššÈ¥ šÎ šŠŠ šš Ú š šš õñ¡š Š õ¯š ÚšÇ ŠÏŠŠ õ¯š¥ŠÀ õñ¡ Ú˜õ¡¯Š šÊš˜õ¯š
 šÇŠÊ. šÇŠÊ.
- šÊš˜õ¯(ð¡ÙÍ¢ÒÏ, central angle)-šš Š Š¯šÏŠÎšÇ ŠÏŠŠ õ¯ ŠŠ õñ¡Š˜Ú õ¯š õ¯Š ŠÚš õ¯
- õ¥ÙšÏõ¯(--ÒÏ, =š õ¯(Õ ÒÏ), vertical angle)
- õ瘊ˋÇõ¯(ÓÕÂÒÏ, spherical angle, =õ°çŠˋÇõ¯)
Ú¿šõ¯õ°¥ š¥Š¯õ¯
- Ú¿šõ¯š š¥õ¯Ú´ššš ŠÚŠŠ 0ù, 15ù, 30ù, 45ù, 60ù, 75ù, 90ùŠË¥ õ¯ŠÎ˜ÚÊŠˋ¯ šÇŠÀ š¡ÚÇ Š´ššššš š š¥õ¯Ú, š š˜õ¯Ú ŠÝš š˜šˋÚÇ õñ¡ š¥õ¯Š¿ŠË¥ š ŠÚš˜ š£š š šŠÊ. šÇŠ˜Ú Ú¿Š°Ú õ¯ŠÊš¡ Ú¿šõ¯ŠÊš š¥õ¯Ú´šŠÝšš ŠÏÊš¯ šÊšÚ šÝšÏš õ¯ŠŠÊ.
Š´ššššš 0ù,30ù, 45ù, 60ù, 90ùš ŠÇõ¯š¥ŠÀ õ¯Š š š¥õ¯Ú, šÇŠÝŠ°š¥õ¯Ú, š š˜õ¯Úš šŠš õ¯šÇ 0ù,30ù, 45ù, 60ù, 90ùš õñ¡š šÈ¥õ¡¯š š¡ õ¯Š 120ù,135ù,150ù,180ù,....ŠÝšš š¥õ¯Ú´šŠË¥ š£õý Úǚȥõ¡¯š Ú¿Š°Ú õ¯š¥ŠÀ ŠÑŠÎ¯ŠÊ. õñ¡ŠÎ˜õ° 15ùš 75ùŠ š¥õ¯Ú´šš ŠÏš
š ŠÎ˜ŠÀ š ŠÚ š šŠÊ.
| Ú¿šõ¯ |
š˜š¡ |
š§š˜š¡ |
Úš Ú¡
|
| 0ù
|
 |
 |

|
| 15ù
|
 |
 |

|
| 30ù
|
 |
 |

|
| 45ù
|
 |
 |

|
| 60ù
|
 |
 |

|
| 75ù
|
 |
 |

|
| 90ù
|
 |
 |

|
- š¥Š¯õ¯š ššš Š¯šÏš š õ¡¯šÊš (šÑ)š¥ŠÀÚÇš õñ¡õýõ°¥ šš š õ¥ÙšÏš š¥ŠÀ õ°çš ÚŠ ŠŠÊŠË¡ Š¯šÏš (Šõý§ š )šÇ šÇŠÈ´Š õ¯ ŠŠ šÇŠ˜Ú õ¯õ°¥ õñ¡ Šõý§š š Úš š¥ŠÀ š£šÇšÏ õ¯š ÚˋÚš˜ ŠÚŠÇŠ õ¯š õ¯ŠÎ˜Ú´ŠÊ. š¥Š¯õ¯š 360ùn+öÝ(nš šŠŠ Úš Úš ,öÝŠ õ¯Š, Ú¡ŠŠýš¥ŠÀŠ 2ün+öÝ)šýŠ¥ ÚÚŠŠÊ.
Š´š
- Š(degree): õ¡¯Ú¡Š ùšÇŠˋ¯ Ú Úš š 360ŠÝŠÑÚ õýšÇŠÊ.
- ŠÑ(minute): õ¡¯Ú¡Š 'šÇŠˋ¯ 1ŠŠË¥ 60ŠÝŠÑÚ õýšÇŠÊ.
- šÇ(second): õ¡¯Ú¡Š "šÇŠˋ¯ 1ŠÑš 60ŠÝŠÑÚ õýšÇŠÊ.
- Š¥Šš(radian, rad): õ¡¯Ú¡Š Š°ÇÚç š¯šÏ šš¥Šˋ¯ ŠÑšÝõ¥Çš Ú¡š Š¯šÏŠÎš Š¿šÇŠÊ.
- šÊÚ
Š¥Šš(steradian,sr), ÚŠ¯ˋŠ¥Šš(square radian, radôý): š
šýÇõ¯š Š´šŠÀ, õ瘚 š¥ŠÑš ŠËõñ¥ ŠÑŠÑš ŠšÇš Š¯šÏŠÎš š õ°Ýš Š¿šÇŠÊ.
- ÚŠ¯ˋŠ(square degree, degôý, (ô¯)ôý):š
šýÇõ¯š Š´š.
šÇŠÊ š˜šÇš Úš¯ õÇõ°Š ŠÊšõ°¥ õ¯ŠÊ.
  - (ü/180)ôýsr =1(ô¯)ôý
- 32400/üôýdegôý=1radôý
Ú¿šÏ
- š ÚNJΘŠ ÚŠˋÇš šŠ š¥õ¯Úš ŠÇõ¯š Úˋš
 šÇŠÊ. šÇŠÊ.
- š ÚNJΘŠ ÚŠˋÇš šŠ nõ¯Úš ŠÇõ¯š Úˋš
 šÇŠÊ. šÇŠÊ.
Š šÏš šÇ ÚÚÚ Š, Ššõ¯š Ú˜õ¡¯Š õ¯ŠÊ.
Š šÏš šÇ ÚÚÚ Š, šõ¯š Ú˜õ¡¯Š õ¯ŠÊ.
Šš¡ÀŠÇõ¯š Úˋš 180ô¯šÇŠÊ.
õ¡¯Ú šˋšÇ
- õý§š˜õ¯(̓ÌÒÏ, tilt angle): õ¡¯š¡õ¡¯(õý§š˜)õ¯ šŠ õ¯Š
- õ° õ¯(Õ¨ÒÏ, =š˜Š ÊŠ°¡õ¯, šõ¯(ð£¯ÒÏ) altitude, high[wide, vertical] angle): ÚÚŠ š¿ÇŠˋŠ¥ šÇ˜š ŠÝšš ŠÊŠÈ´šÇšÏŠÊ.
- õÇõ¯(Í
ÒÏ, optic angle): õÇõ¯ŠÏš¥
- õÇõ¯(Í£ÈÒÏ, wide-angle): õÇõ¯ Š šÎ, õÇõ¯ Xš š¯Š
- õÇšÑõ¯(Í
Ò£¡ÒÏ, optic angle)
- õçÇš õ¯(ÍÝÌÒÏ, refracting angle): š
š˜õ¯šÇŠ ŠÑš¯šš õݯŠÀ ŠŠÊ.
- ŠˋÇõ¯(ÕÂÒÏ, face angle)
- Š¯š˜õ¯(ÍͯÒÏ)
- Š¯ˋÚËõ¯(Ì¿ÍÒÏ, direction angle)
- Š°çõ¯(ð¥ÒÏ, dip, inclination)
- ŠÑõ¯(ð¢₤ÒÏ, =ŠÇŠ ÊŠ°¡õ¯, dip, angle of depression[declination]): ÚÚŠ š¿ÇŠˋŠ¥ šÇ˜š ŠÝšš ŠÊŠÈ´šÇšÏŠÊ.
- š˜õ¯(ÌÙ£ÒÏ, dead angle): š˜õ¯šÏŠ õý§õ° šËš¿šššýŠ¥ šš¥šš õ¯ŠÎ˜šš ¡ Š°ÇšÇšÏ šŠ ššÙš š˜õ¯šÏŠŠ¥õ° š¿ÙÚŠÊ.
- šŠ¯õ¯(ð¡ÍÒÏ, dihedral angle)
- šõ¯(ÒÎÒÏ, visual angle): šÚÊŠÝŠÏš˜š šõ¯3 š¯¡šÀ¯
- šõ¯(ÌÒÏ, hour angle): šÚÊŠÝŠÏš˜š šõ¯1 š¯¡šÀ¯
- šš¯´(ÒÎÍñÛ, parallax): šš¯´ (šýŠ˜¡Ú)
- šÊšõ¯(ÍÊÝÕÒÏ)
- šŠˋÇõ¯(ÕÀÕÂÒÏ, facial angle)
- šõ¯(Ò¢ÒÏ, =Š õ¯õ¯, angle of incidence[attack], attck angle) = Š¯šõ¯
- ššõ¯(ð§Ó¡ÒÏ, phase angle): ššõ¯
- šõ°õ¯(Ò´ÓÒÏ, =Úõ°õ¯, critical angle): š Š¯š˜ ŠŠ šÊõ¯ÚŠÎ˜šÎ ŠÝšš õݯŠÀ ŠŠÊ.
- š
š˜õ¯(Í
ËͯÒÏ, =Ú˜š˜õ¯)
- ššÊõ¯(ÍÙÍÒÏ, meridian angle)
- šÀ¯õ¯(Ó
ÏÒÏ, glancing angle)
- š¯ˋŠËõ¯(ÓÕ¡ÒÏ, landing angle)
- Ú¡õ¯(ÍÒÏ, polar angle): Ú¡õ¯ (šÚ)
- ÚŠ¯õ¯(ð¡ÍÒÏ)
- ÚšÝ šõ¯(ÌÒÏ, sidereal hour angle)
- Úõ°çõ¯(Ì£Óˋ¤ÒÏ, glide slope, gliding angle): Úõ°çõ¯ šÏšõ¡¯ Š¯ šÚšš¡ šÏšõ° ŠÝšš ŠÊŠÈ´šÇšÏŠÊ.
õ¯šÇ Š°Çõ¡¯
õ¯šÈ¥
|
|